Sie sind hier: ICP » R. Hilfer » Publikationen

4 Inverse Mittag-Leffler functions

[647.7.1] We introduce the inverse generalized Mittag-Leffler functions Lα,β⁢z as the solutions of the equation

Lα,β⁢Eα,β⁢z=z.(43)

[647.7.2] Our ability to calculate Eα,β⁢z allows us to evaluate also Lα,β⁢z by solving this functional equation numerically. [647.7.3] We have succeeded to determine the principal branch of Lα,β⁢z in such a way that three conditions are fulfilled. [647.7.4] 1. The function Lα,β⁢z is single valued and well defined on its principal branch. [647.7.5] 2. Its principal branch reduces to the principal branch of the logarithm for α→1. [647.7.6] 3. Its principal branch is a simply connected subset of the complex plane. 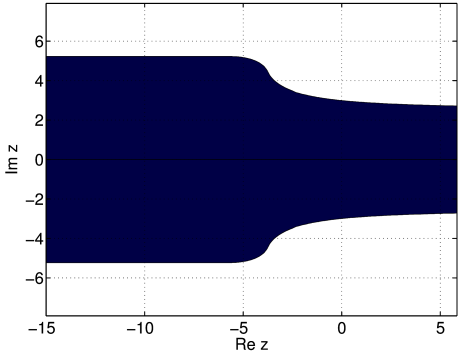[647.7.7] Figure 15 shows the principal branch for the case α=0.95, β=1.

Figure 15: The dark region corresponds to the principal branch of the inverse generalized Mittag-Leffler function Lα,β⁢z for α=0.95, β=1.