Article
[page 281, §1]
[281.1.1] A universality class in the theory of critical phenomena is
identified by a set of critical exponents and a set of universal
scaling functions [1, 2, 3].
[281.1.2] In practice finite size scaling functions and their associated
universal amplitudes or amplitude ratios have become an
indispensable tool for the extraction of universal behaviour
from numerical simulations of finite systems throughout many
fields of physics [4, 5, 6, 7, 8], and
the subject remains of vigorous research interest
[9, 10, 11, 12].
[281.1.3] It is therefore of broad interest
to obtain exact information on finite size scaling functions.
[281.1.4] Such knowledge would also be particularly important for discerning
corrections to scaling behaviour.
[281.2.1] Most determinations of critical finite size scaling
functions or amplitude ratios have been carried out by
numerical simulation of critical systems
[3, 13, 14, 15, 16, 17, 18, 19, 20, 21].
[281.2.2] Analytical calculations [22, 23, 24, 25] are complicated
because at criticality the influence of boundary conditions
cannot be neglected.
[281.2.3] This renders renormalization group methods
difficult to implement.
[281.2.4] The problem of hyperscaling violations [26, 27] has further obscured the basic question as to
what extent finite size scaling functions are universal or not.
[281.2.5] Recently [28], however, finite size scaling theory has been reanalysed from the perspective of
a general classification theory for phase transitions [29, 30, 31, 32, 33].
[281.2.6] In these papers it was shown that phase transitions in statistical mechanics may be classified according
to a generalized classification theory.
[281.2.7] This theory classifies each transition according to its
generalized order in analogy with Ehrenfest’s classification scheme.
[281.2.8] The objective of the present letter is to compare analytical predictions
of the generalized classification scheme with computer simulation results.
[281.2.9] The comparison is carried out for the critical finite size scaling
function of the order parameter distribution in the two- and three
dimensional Ising models with periodic boundary conditions.
[281.2.10] Good agreement between simulations and the theoretical predictions is
found over the entire range for which numerical data are available.
[page 282, §1]
[282.1.1] Define pψ,L,ξ to be the probability density function for
the fluctuating order parameter Ψ in a finite system of size L and
order parameter correlation length ξ.
[282.1.2] Then the scaling function of interest p~x,y is defined by
| pψ,L,ξ=LddΨ-d*/d-d*p~ψLddΨ-d*/d-d*,L/ξd* | | (1) |
where dΨ is the anomalous or scaling dimension of the order
parameter, d* is Fishers anomalous dimension of the vacuum [34],
and ξd* is Binders thermodynamic length [35].
[282.1.3] If hyperscaling holds then d*=0, the thermodynamic length becomes
the correlation length, ξ0=ξ, and the exponent in (1)
reduces to the familiar form dΨ=β/ν where
β is the order parameter exponent and ν the correlation
length exponent.
[282.1.4] The scaling function p~x,y is expected to be universal
up to the choice of boundary conditions [13].
[282.2.1] Given the scaling Ansatz (1) the traditional scaling analysis [13, 25]
of the critical scaling function p~x,0 distinguishes two cases.
(i)
[282.2.2] For x≪1 the scaling function is expected to have the universal
Landau-Ginzburg form [13]
| p~x,0∝exp-A0-A2x2-A4x4-…. | | (2) |
(ii)
[282.2.3] For x≫1 and groundstate boundary conditions (e.g. all
spins positive for the Ising model) the scaling function is expected
to have the squeezed exponential form [36]
where δ denotes the equation of state exponent.
[282.2.4] Based on scaling arguments the same form is expected to apply for periodic
boundary conditions [25].
[282.3.1] Little exact information is available for p~x,0.
[282.3.2] To the best of our knowledge only the cumulant ratio
g0=∫x4p~x,0dx/∫x2p~x,0dx2
for the two dimensional Ising model with singular periodic boundary
conditions has been calculated exactly [24].
[282.3.3] For noncritical systems on the other hand the analogous noncritical
scaling function is Gaussian by virtue of the central limit theorem [13].
[282.3.4] The absence of exact information about the critical
function p~x,0 even for the otherwise
exactly solvable two dimensional Ising model is related
to the absence of its solution in nonzero magnetic field [36].
[282.4.1] Recently the universal part of critical finite size scaling functions
has been related to finite ensemble scaling functions [33, 28].
[282.4.2] Finite ensemble scaling functions arise in the ensemble limit while
finite size scaling functions arise in the finite size scaling limit.
[282.4.3] For a d-dimensional discretized lattice system in the fully finite
hypercubic geometry the finite size scaling limit is defined as
the limit limL,ξ→∞L/ξ=c in which the box dimension L and the correlation
length ξ increase to infinity in such a way that their ratio remains constant.
[282.4.4] In the ensemble limit on the other hand the lattice constant a approaches 0 simultaneously.
[282.4.5] More precisely, the ensemble limit is defined as the limit limM,N→∞N/M=c
in which M=ξ/ad and N=L/ξd approach infinity
such that their ratio remains constant.
[282.5.1] In the finite size scaling limit the critical finite size scaling functions
are found to contain a universal as well as a nonuniversal part.
[282.5.2] The universal part is given by the finite ensemble scaling functions which arise
in the finite ensemble limit and for which analytical
expressions can be derived if the scaling dimension of the
critical operator in question is known.
[282.5.3] For a critical operator X at the critical point of a d-dimensional system with Ising symmetry
and periodic boundary conditions the universal part of the critical
finite size scaling function is written as [28]
| p~x,0=12h+x;ϖX+12h-x;ϖX | | (4) |
[page 283, §0]
with
where αX is the thermodynamic fluctuation exponent [34] of the observable X.
[283.0.1] If X represents the energy density then
αE=α, the specific heat exponent, while for the
order parameter density αΨ=1-1/δ where δ
is the equation of state exponent.
[283.0.2] The scaling functions h±x;ϖX obey
h+x=h--x and can be written in terms of the H-function
representation of stable probability densities [37, 38, 39] as
| h(x;ϖX)=1ϖXH1110(x|1-1/ϖX,1/ϖX0,1). | | (6) |
[283.0.3] The general class of H-functions is usually defined in terms of
Mellin-Barnes contour integrals and contains Meijer’s G-function
as well as many other generalized hypergeometric functions as special cases.
[283.0.4] For a precise definition we refer the reader to standard tables [38].
[283.0.5] Note that equation (6) depends only on ϖX
which is completely determined by the scaling dimension of X.
[283.0.6] Note also that equations (4) and (6)
apply for periodic boundary conditions.
[283.0.7] The general theory identifies a universal shape and symmetry parameter which is related
to different choices of boundary conditions [28].
[283.0.8] It was identified in [28] to be unity for periodic
boundary conditions and the same choice has been applied here.
[283.0.9] In the following we focus on order parameter fluctuations, i.e. X=Ψ.
[283.0.10] In that case the index ϖX becomes ϖΨ=1+1/δ
where δ is the equation of state exponent.
[283.1.1] The scaling function given by (4) and (6) are
consistent with the scaling results (2) and (3).
[283.1.2] The functions h±x;ϖX are entire functions of x,
and thus p~x,0 may be expanded around x=0 as
assumed in (2).
[283.1.3] Secondly the asymptotic expansion of
the H-functions [40] gives
| h±x;ϖΨ∝xδ-1/2exp-1δδxδ+1δ+1 | | (7) |
which is consistent with the scaling result (3) even
though it is not derived in the same scaling limit.
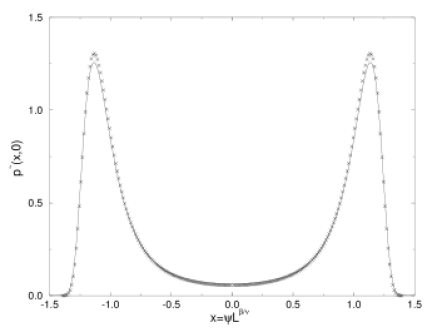
[283.2.1] In Figure 1a we compare the analytical result to simulation
data for the two dimensional Ising model with periodic boundary conditions.
[283.2.2] In this case δ=15 and the critical temperature is known exactly.
[283.2.3] The simulation results are represented as crosses,
the analytical result as a solid line.
[283.2.4] The crosses give a smoothed representation of scaled simulation data [19]
for system size L=64.
[283.2.5] All distributions are scaled to unit norm and variance.
[283.2.6] For the analytical curve this requires a cutoff which was chosen
at a value close to the largest simulation data point.
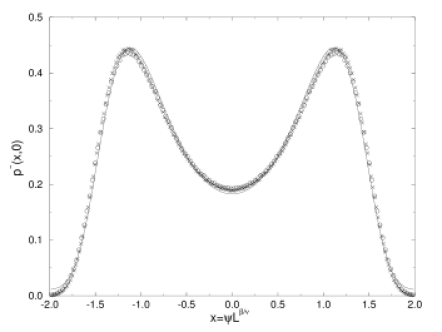
[283.3.1] In Figure 1b the same comparison is shown for the case of the d=3 Ising model.
[283.3.2] In this case neither the critical temperature
nor the equation of state exponent δ are known exactly.
[283.3.3] The data points represent original high precision Monte Carlo simulations in which systems
of size L=20 and L=32 were studied for 50×106
Monte Carlo sweeps each using a vectorized code on a Cray YMP.
[283.3.4] The data for the system size L=20 is represented by crosses, that for L=32 by circles.
[283.3.5] We used the estimates [20] J/kBTc=0.2216595 for the critical temperature and
δ=4.8 for the equation of state exponent.
[283.3.6] Here J denotes the Ising exchange coupling and kB is Boltzmann’s constant.
[283.4.1] The agreement between the analytical prediction and the simulation
results in both two and three dimensions is gratifying.
[283.4.2] We attribute the small discrepancies, in part at least, to
[page 284, §0]
the low statistics in the tails of the scaling function.
[284.0.1] This view is supported by comparing the scaling function obtained in
a previous small-scale study of the 3D Ising model [13], with
that of figure 1(b).
[284.0.2] While both the scaling functions of [13] and those reported here
exhibit excellent data collapse, the scaling functions in both cases
are markedly different, demonstrating the presence of the nonuniversal
part [28].
[284.0.3] The good agreement between theory and simulations lends
substantial support to the theoretical ideas from which the scaling functions derive.
[284.0.4] In particular it should be emphasized that the
only difference between the solid lines in Figure 1a and 1b is the value of δ.
[284.0.5] This suggests that the full functional form
of the universal part of the critical finite size scaling function
of the order parameter distribution could in simple cases be determined
by a few universal parameters, most notably the equation of state exponent.
[284.0.6] Further numerical and analytical studies are, however,
required to conclusively establish whether the proposed
universal scaling functions
[page 285, §0]
agree fortuitously with the
Monte Carlo data or are more generally correct.