| 1 |
H.E. Stanley.
Introduction to Phase Transitions and Critical Phenomena.
Oxford University Press, New York, 1971.
|
| 2 |
M.E. Fisher.
Scaling, universality and renormalization group theory.
In F.J.W. Hahne, editor, Critical Phenomena, page 1, Berlin,
1983. Springer Verlag.
|
| 3 |
A.D. Bruce.
Universality in the two-dimensional continuous spin model.
J. Phys. A: Math. Gen., 18:L873, 1985.
|
| 4 |
J.L. Cardy (ed.).
Finite-Size Scaling.
North-Holland, Amsterdam, 1988.
|
| 5 | K. Binder and D.W. Heermann.
Monte Carlo Simulation in Statistical Physics.
Springer Verlag, Berlin, 1988.
|
| 6 |
V. Privman (ed.).
Finite-Size Scaling and Numerical Simulation of Statistical
Systems.
World Scientific, Singapore, 1990.
|
| 7 |
V. Privman, P.C. Hohenberg, and A. Aharony.
Universal critical point amplitude relations.
In C. Domb and J.L. Lebowitz, editors, Phase Transitions and
Critical Phenomena, volume 14, page 1, London, 1991. Academic Press.
|
| 8 |
H. Gausterer and C. Lang (eds.).
Computational Methods in Field Theory.
Springer, Berlin, 1992.
|
| 9 |
K.T. Leung.
Finite size scaling of driven diffusive systems – theory and
Monte-Carlo studies.
Phys.Rev.Lett., 66:453, 1991.
|
| 10 |
M. Krech and S. Dietrich.
Finite size scaling for critical films.
Phys.Rev.Lett., 66:345, 1991.
|
| 11 |
A.D. Bruce and N.B. Wilding.
Scaling fields and universality of the liquid-gas critcal point.
Phys.Rev.Lett., 68:193, 1992.
|
| 12 |
J.-K. Kim.
Application of finite size scaling to Monte Carlo simulations.
Phys.Rev.Lett., 70:1735, 1993.
|
| 13 |
K. Binder.
Finite size scaling analysis of Ising model block distribution
functions.
Z.Phys.B, 43:119, 1981.
|
| 14 |
K. Kaski, K. Binder, and J.D. Gunton.
Study of cell distribution functions of the three-dimensional Ising
model.
Phys.Rev.B, 29:3996, 1984.
|
| 15 |
A.D. Bruce, T. Schneider, and E. Stoll.
Phys. Rev. Lett., 43:1248, 1979.
|
| 16 |
J.L. Cardy.
Conformal invariance.
In C. Domb and J.L. Lebowitz, editors, Phase Transitions and
Critical Phenomena, volume 11, page 55, London, 1987. Academic Press.
|
| 17 |
B. Derrida, B.W. Southern, and D. Stauffer.
J.Phys.(Paris), 48:335, 1987.
|
| 18 |
A. Sariban and K. Binder.
Critical properties of the Flory Huggins model of polymer
mixtures.
J. Chem. Phys., 86:5859, 1987.
|
| 19 | D. Nicolaides and A.D. Bruce.
Universal configurational structure in two-dimensional scalar models.
J. Phys. A: Math. Gen., 21:233, 1988.
|
| 20 |
A.M. Ferrenberg and D.P. Landau.
Critical behaviour of the three dimensional Ising model: A
high-resolution Monte Carlo study.
Phys.Rev. B, 44:5081, 1991.
|
| 21 |
N. B. Wilding and A.D. Bruce.
Density fluctuations and field mixing in the critical fluid.
J. Phys.: Condens. Matter, 4:3087, 1992.
|
| 22 |
A.D. Bruce.
Probability density functions for collective coordinates in
Ising-like systems.
J. Phys. C, 14:3667, 1981.
|
| 23 |
E. Brezin and J. Zinn-Justin.
Finite size effects in phase transitions.
Nucl.Phys., B257:867, 1985.
|
| 24 |
T.W. Burkhardt and B. Derrida.
Moments of the total magnetization and conformal invariance in the
finite twodimensional Ising model.
Phys. Rev. B, 32:7273, 1985.
|
| 25 |
E. Eisenriegler and R. Tomaschitz.
Helmholtz free energy of finite spin systems near criticality.
Phys.Rev.B, 35:4876, 1987.
|
| 26 |
E. Brezin.
An invesitgation of finite size scaling.
J. Physique, 43:15, 1982.
|
| 27 |
K. Binder, M. Nauenberg, V. Privman, and A.P. Young.
Finite size tests of hyperscaling.
Phys. Rev. B, 31:1498, 1985.
|
| 28 |
R. Hilfer.
Absence of hyperscaling violations for phase transitions with
positive specific heat exponent.
Z. Physik B, 96:63, 1994.
|
| 29 |
R. Hilfer.
Thermodynamic scaling derived via analytic continuation from the
classification of Ehrenfest.
Physica Scripta, 44:321, 1991.
|
| 30 |
R. Hilfer.
Multiscaling and the classification of continuous phase transitions.
Phys. Rev. Lett., 68:190, 1992.
|
| 31 |
R. Hilfer.
Scaling theory and the classification of phase transitions.
Mod.Phys.Lett. B, 6:773, 1992.
|
| 32 |
R. Hilfer.
Classification theory for phase transitions.
Int.J.Mod.Phys.B, 7:4371, 1993.
|
| 33 | R. Hilfer.
Classification theory for anequilibrium phase transitions.
Phys.Rev.E, 48:2466, 1993.
|
| 34 |
M.E. Fisher.
General scaling theory for critical points.
In B. Lundqvist and S.Lundqvist, editors, Collective Properties
of Physical Systems, page 16, New York, 1973. Academic Press.
|
| 35 |
K. Binder.
Some recent progress in the phenomenological theory of finite size
scaling and application to Monte Carlo studies of critical phenomena.
In V. Privman, editor, Finite Size Scaling and Numerical
Simulation of Statistical Systems, page 173, Singapore, 1990. World
Scientific.
|
| 36 |
B.M. McCoy and T.T. Wu.
The Two Dimensional Ising Model.
Harvard University Press, Cambridge, 1972.
|
| 37 |
C. Fox.
The 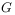 and and 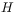 functions as symmetrical Fourier kernels.
Trans. Am. Math. Soc., 98:395, 1961. functions as symmetrical Fourier kernels.
Trans. Am. Math. Soc., 98:395, 1961.
|
| 38 |
A.P. Prudnikov, Yu.A. Brychkov, and O.I. Marichev.
Integrals and Series, volume 3.
Gordon and Breach, New York, 1990.
|
| 39 |
W.R. Schneider.
Stable distributions: Fox function representation and generalization.
In S. Albeverio, G. Casati, and D. Merlini, editors, Stochastic
Processes in Classical and Quantum Systems, page 497, Berlin, 1986. Springer
Verlag.
|
| 40 |
B.L.J. Braaksma.
Asymptotic expansions and anlytic continuations for a class of
Barnes-integrals.
Compos.Math., 15:239, 1964.
|
