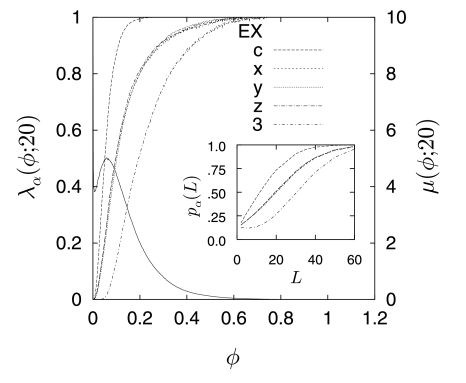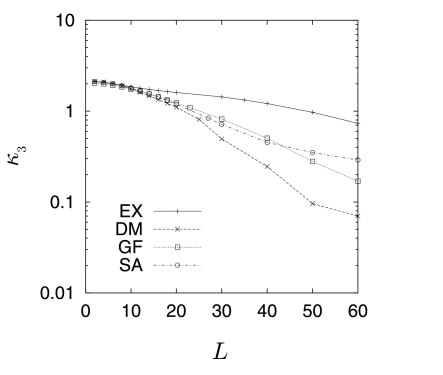5 Quantitative Comparison of Microstructures

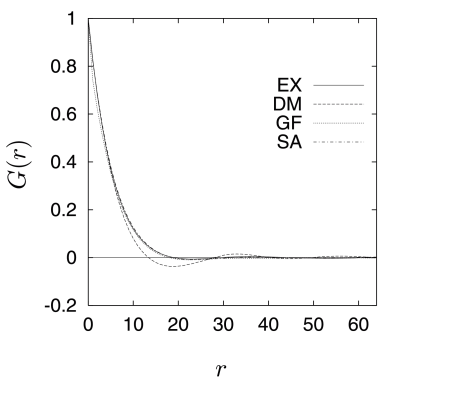
[228.1.1] Table 2 gives an overview of several geometric properties for the four microstructures discussed in the previous section. [228.1.2] Samples GF  and SA  were constructed to have the same correlation function as sample EX. [228.1.3] Figure 7 shows the directionally averaged correlation functions G⁢r=G⁢r,0,0+G⁢0,r,0+G⁢0,0,r/3 of all four microstructures where the notation G⁢r1,r2,r3=G⁢r was used.

[228.2.1] The Gaussian field reconstruction GGF⁢r is not perfect and differs from GEX⁢r for small r. [228.2.2] The discrepancy at small r reflects the quality of the linear filter, and it is also responsible for the differences of the porosity and specific internal surface. [228.2.3] Also, by construction, GGF⁢r is not expected to equal GEX⁢r for r larger than 30. [228.2.4] Although the reconstruction method of sample SSA is intrinsically anisotropic the correlation function of sample SA  agrees also in the diagonal directions with that of sample EX. [228.2.5] Sample SDM while matching the porosity and grain size distribution was not constructed to match also the correlation function. [228.2.6] As a consequence GDM⁢r differs clearly from the rest. [228.2.7] It reflects the grain structure of the model by becoming negative. [228.2.8] GDM⁢r is also anisotropic.

[page 229, §1]    [229.1.1] If two samples have the same correlation function they are expected to have also the same specific internal surface as calculated from

[229.1.2] The specific internal surface area calculated from this formula is given in Table 2 for all four microstructures.

[229.2.1] If one defines a decay length by the first zero of the correlation function then the decay length is roughly 18⁢a for samples EX, GF  and SA. [229.2.2] For sample DM  it is somewhat smaller mainly in the x- and y-direction. [229.2.3] The correlation length, which will be of the order of the decay length, is thus relatively large compared to the system size. [229.2.4] Combined with the fact that the percolation threshold for continuum systems is typically around 0.15 this might explain why models GF  and SA  are connected in spite of their low value of the porosity.

[229.3.1] In summary, the samples SGF and SSA were constructed to be indistinguishable with respect to porosity and correlations from SEX. [229.3.2] Sample SA  comes close to this goal. [229.3.3] The imperfection of the reconstruction method for sample GF  accounts for the deviations of its correlation function at small r from that of sample EX. [229.3.4] Although the difference in porosity and specific surface is much bigger between samples  SA  and  GF  than between samples  SA  and  EX  sample  SA  is in fact more similar to  GF  than to  EX  in a way that can be quantified using local porosity analysis. [229.3.5] Traditional characteristics such as porosity, specific surface and correlation functions are insufficient to distinguish different microstructures. [229.3.6] Visual inspection of the pore space indicates that samples GF  and SA  have a similar structure which, however, differs from the structure of sample EX. [229.3.7] Although sample DM  resembles sample EX  more closely with respect to surface roughness it differs visibly in the shape of the grains.

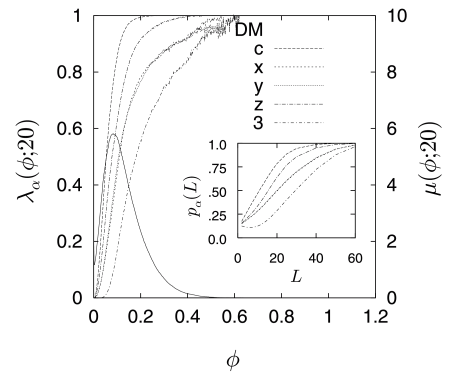
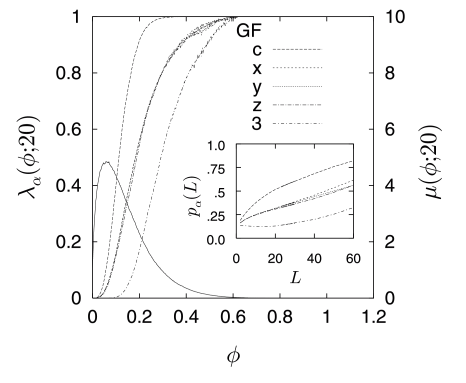
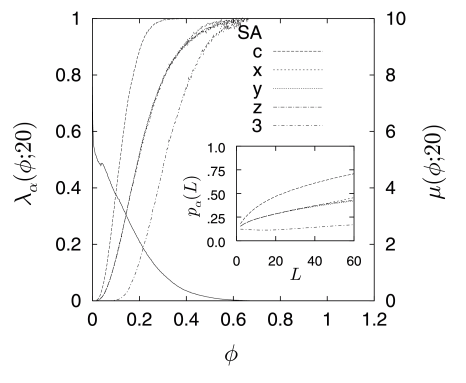
[229.3.8] The differences in visual appearance of the four microstructures can be quantified using the geometric observables μ and λ from local porosity theory. [229.3.9] The local porosity distributions μ⁢ϕ,20 of the four samples at L=20⁢a are displayed as the solid lines in Figures 8a through 8d. [229.3.10] The ordinates for these curves are plotted on the right vertical axis.

[229.4.1] The figures show that the original sample exhibits stronger porosity fluctuations than the three model samples except for sample SA  which comes close. [229.4.2] Sample DM  has the narrowest distribution which indicates that it is most homogeneous. [229.4.3] Figures 8a–8d show also that the δ-function component at the origin, μ⁢0,20, is largest for sample EX, and smallest for sample GF. [229.4.4] For samples DM  and SA  the values of μ⁢0,20 are intermediate and comparable. [229.4.5] Plotting μ⁢0,L as a function of L shows that this remains true for all L. [229.4.6] These results indicate that the experimental sample EX  is more strongly heterogeneous than the models, and that large regions of matrix space occur more frequently in sample EX. [229.4.7] A similar conclusion may be drawn from the variance of local porosity

[page 230, §0]

[page 231, §0]

[page 232, §0]    fluctuations which will be studied below. [232.0.1] The conclusion is also consistent with the results for L* shown in Table 2. [232.0.2] L* gives the sidelength of the largest cube that can be fit into matrix space, and thus L* may be viewed as a measure for the size of the largest grain. [232.0.3] Table 2 shows that the experimental sample has a larger L* than all the models. [232.0.4] It is interesting to note that plotting μ⁢1,L versus L also shows that the curve for the experimental sample lies above those for the other samples for all L. [232.0.5] Thus, also the size of the largest pore and the pore space heterogeneity are largest for sample EX. [232.0.6] If μ⁢ϕ,L* is plotted for all four samples one finds two groups. [232.0.7] The first group is formed by samples EX  and DM, the second by samples GF  and SA. [232.0.8] Within each group the curves μ⁢ϕ,L* nearly overlap, but they differ strongly between them.

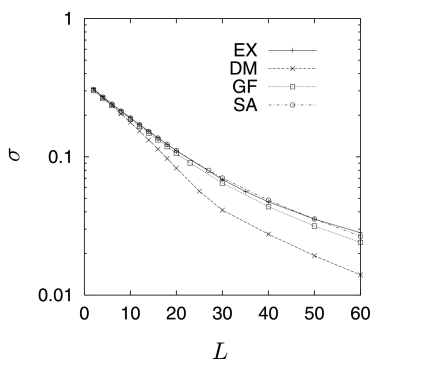
[232.1.1] Figures 9, and 10 exhibit the dependence of the local porosity fluctuations on L.

[232.1.2] Figure 9 shows the variance of the local porosity fluctuations, defined in (40) as function of L. [232.1.3] The variances for all samples indicate an approach to a δ-distribution according to (43). [232.1.4] Again sample DM  is most homogeneous in the sense that its variance is smallest. [232.1.5] The agreement between samples EX, GF  and SA  reflects the agreement of their correlation functions, and is expected by virtue of eq. (40). [232.1.6] Figure 10 shows the skewness as a function of L calculated from (41). [232.1.7] κ3 characterizes the asymmetry of the distribution, and the difference between the most probable local porosity and its average. [232.1.8] Again samples GF  and SA  behave similarly, but sample DM  and sample EX  differ from each other, and from the rest.

[page 233, §1]    [233.1.1] At L=4⁢a the local porosity distributions μ⁢ϕ,4 show small spikes at equidistantly spaced porosities for samples EX  and DM, but not for samples GF  and SA. [233.1.2] The spikes indicate that models EX  and DM  have a smoother surface than models GF  and SA. [233.1.3] For smooth surfaces and small measurement cell size porosities corresponding to an interface intersecting the measurement cell produce a finite probability for certain porosities because the discretized interface allows only certain volume fractions. [233.1.4] In general whenever a certain porosity occurrs with finite probability this leads to spikes in μ.

[233.1.5] Visual inspection of Figures 1 through 4 does not reveal the degree of connectivity of the various samples. [233.1.6] A quantitative characterization of connectivity is provided by local percolation probabilities [27, 10], and it is here that the samples differ most dramatically.

[233.2.1] The samples EX, DM , GF  and SA  are globally connected in all three directions. [233.2.2] This, however, does not imply that they have similar connectivity. [233.2.3] The last line in Table 2 gives the fraction of blocking cells at the porosity 0.1355 and for L*. [233.2.4] It gives a first indication that the connectivity of samples DM  and GF  is, in fact, much poorer than that of the experimental sample EX.

[233.3.1] Figures 8a through 8d give a more complete account of the situation by exhibiting λα⁢ϕ,20 for α=3,c,x,y,z for all four samples. [233.3.2] First one notes that sample DM  is strongly anisotropic in its connectivity. [233.3.3] It has a higher connectivity

[page 234, §0]    in the z-direction than in the x- or y-direction. [234.0.1] This was found to be partly due to the coarse grid used in the sedimentation algorithm [47]. [234.0.2] λz⁢ϕ,20 for sample DM  differs from that of sample EX  although their correlation functions in the z-direction are very similar. [234.0.3] The λ-functions for samples EX  and DM  rise much more rapidly than those for samples GF  and SA. [234.0.4] The inflection point of the λ-curves for samples EX  and DM  is much closer to the most probable porosity (peak) than in samples GF  and SA. [234.0.5] All of this indicates that connectivity in cells with low porosity is higher for samples EX  and DM  than for samples GF  and SA. [234.0.6] In samples GF  and SA  only cells with high porosity are percolating on average. [234.0.7] In sample DM  the curves λx,λy and λ3 show strong fluctuations for λ≈1 at values of ϕ much larger than the ϕ or ϕ⁢SDM. [234.0.8] This indicates a large number of high porosity cells which are nevertheless blocked. [234.0.9] The reason for this is perhaps that the linear compaction process in the underlying model blocks horizontal pore throats and decreases horizontal spatial continuity more effectively than in the vertical direction, as shown in [4], Table 1 p. 142.

[234.1.1] The absence of spikes in μ⁢ϕ,4 for samples GF  and SA  combined with the fact that cells with average porosity (≈0.135) are rarely percolating suggests that these samples have a random morphology similar to percolation.

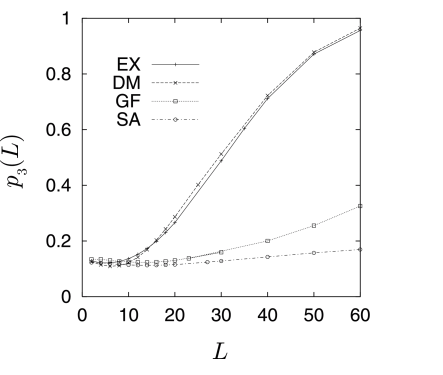
[234.2.1] The insets in Figures 8a through 8d show the functions pα⁢L=λα⁢ϕ,L¯ for α=3,x,y,z,c for each sample calculated from (53). [234.2.2] The curves for samples EX  and DM  are similar but differ from those for samples GF  and SA. [234.2.3] Figure 11 exhibits the curves p3⁢L of all four samples in a single figure. [234.2.4] The samples fall into two groups {EX,DM} and {GF,SA} that behave very differently. [234.2.5] Figure 11

[page 235, §0]    suggests that reconstruction methods [1, 70] based on correlation functions do not reproduce the connectivity properties of porous media. [235.0.1] As a consequence, one expects that also the physical transport properties will differ from the experimental sample, and it appears questionable whether a pure correlation function reconstruction can produce reliable models for the prediction of transport.

[235.1.1] Preliminary results [42] indicate that these conclusions remain unaltered if the linear and/or spherical contact distribution are incorporated into the simulated annealing reconstruction. [235.1.2] It was suggested in [70] that the linear contact distribution should improve the connectivity properties of the reconstruction, but the reconstructions performed by [42] seem not to confirm this expectation.