Sie sind hier: ICP » R. Hilfer » Publikationen

3 Discussion

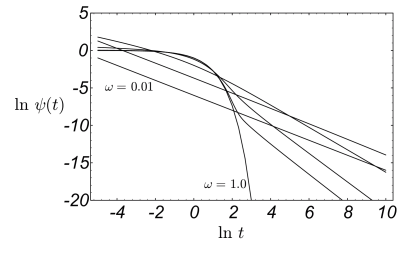
[3.1.1.1] In Figure 1 we display the function ψ⁢t;ω,C for C=1 and ω=0.01,0.1,0.5,0.9,0.99 in a log-log plot. [3.1.1.2] The asymptotic behaviour (2.18) and (2.20) is clearly visible from the figure. [3.1.1.3] The fractional order ω of the time derivative in (1.1) is restricted to 0<ω≤1 as a result of the general theory [3]. [3.1.1.4] This and the behaviour of ψ⁢t in figure 1 attributes special significance to the two limits ω→1 and ω→0.

[3.1.2.1] In the limit ω→1 the fractional master equation (1.2) reduces to the ordinary master equation, and the waiting time density becomes exponentialψ⁢t;1,1=exp⁡-t. [3.2.0.1] In the limit →0 on the other hand equation (1.1) reduces to an eigenvalue or fixed point equation for the operator on the right hand side by virtue of ∂0⁡f/∂⁡t0=f.

[3.2.1.1] While this is interesting in itself an even more interesting aspect is that the correspondingwaiting time density ψ⁢t approaches the formψ(t;ω→0,1)∝1/t for which the normalization becomes logarithmically divergent. [3.2.1.2] This signals an onset of localization in this singular limit. [3.2.1.3] It is hoped that our results will stimulate further research into the fractal time concept.

Figure 1: Log-log plot of the waiting time density ψ⁢t;ω,1 for ω=0.01,0.1,0.5,0.9,0.99,1.0. The curves for ω=1.0 and ω=0.01 have been labeled in the figure, the other curves interpolate between them. For ω=1 the waiting time density is exponential ψ⁢t=exp⁡-t and for ω→0 it approaches ψ⁢t→1/t.