Sie sind hier: ICP » R. Hilfer » Publikationen

Article

[page 1, §1]
[1.1.1.1] Amorphous polymers and supercooled liquids near the glass transition temperature are well known to exhibit nonexponential relaxation behaviour in many experiments [1]. [1.1.1.2] Dielectric spectroscopy, viscoelastic modulus measurements, quasielastic light scattering, shear modulus and shear compliance as well as specific heat measurements all show strong deviations from the exponential Debye relaxation function f(t)=\exp(-t/\tau) where \tau is the relaxation time [2].

[1.1.2.1] Most experimental works on glassy dynamics utilize only a small number of empirical nonexponential expressions when fitting to the observed experimental relaxation data. [1.1.2.2] All of these phenomenological fitting formulae are obtained by the method of introducing a fractional “stretching” exponent into the Debye expression in the time or frequency domain. [1.1.2.3] In the time domain this method leads to the “stretched exponential” or Kohlrausch relaxation function given as

f(t)=\exp[-(t/{\tau _{{\beta}}})^{{\beta}}],\quad 0<{\beta}\leq 1, (1)

with exponent {\beta} and time constant {\tau _{{\beta}}} [3].[1.1.2.4] Of course all formulae obtained by the method of stretching exponents are constructed such that they reduce to the exponential Debye expression when the stretching exponent becomes unity. [1.1.2.5] Relaxation in the frequency domain is described in terms of a normalized complex susceptibility

\widehat{\chi}(u)=\frac{\chi(\omega)-\chi _{\infty}}{\chi _{0}-\chi _{\infty}}=1-u{\mathcal{L}}\left\{ f(t)\right\}(u) (2)

where u=-\mbox{i}\omega, \omega is the frequency, \chi(\omega) is a dynamic susceptibility normalized by the corresponding isothermal susceptibility, \chi _{0}=\lim _{{\omega\to 0}}Re\chi(\omega) is the static susceptibility, \chi _{\infty}=\lim _{{\omega\to\infty}}Re\chi(\omega) gives the “instantaneous” response, and {\mathcal{L}}\left\{ f(t)\right\}(u) is the Laplace transform of the relaxation function f(t). [1.1.2.6] Extending the method of stretching exponents to the frequency domain one obtains the Cole-Cole susceptibility [4]

\widehat{\chi}(u)=\frac{1}{1+(u{\tau _{{\alpha}}})^{{\alpha}}},\quad 0<{\alpha}\leq 1, (3)

the Davidson-Cole expression [5]

\widehat{\chi}(u)=\frac{1}{(1+u{\tau _{{\gamma}}})^{{\gamma}}},\quad 0<{\gamma}\leq 1, (4)

or the combined Havriliak-Negami form [6] given in eq. (22) below. [1.2.0.1] Most surprisingly, the analytical transformations between the time and frequency domain for general values of the parameters in these simple analytical expressions seem to be unknown [7], and authors working in the time domain usually employ the stretched exponential function while authors working in the frequency domain use the stretched susceptibilities.

[1.2.1.1] Despite the fact that inserting the Kohlrausch function into equation (2) does not yield (3) or (4) (or the related Havriliak-Negami susceptibility in eq. (22) below) practitioners have tried to establish a relationship between these functions in order to facilitate the transition between the time and the frequency domain [7]. [1.2.1.2] Equally important for practical purposes is the transformation from expressions (3), (4) or (22) in the frequency domain to the corresponding relaxation functions in time [8]. [1.2.1.3] It seems therefore that analytical expressions for the Kohlrausch susceptibility in the frequency domain and for the Havriliak-Negami relaxation functions in the time domain are of general importance and broad interest.

[1.2.2.1] Great research activities have ensued from the observation of Williams and Watts [3] that the Kohlrausch susceptibility, obtained by inserting equation (1) into equation (2), has an analytical expression when {\beta}=1/2. Let me briefly recall their result. [1.2.2.2] One defines the normalized relaxation function as

f(t)=\begin{cases}\phi(t)/\phi(0)&\text{for }t\geq 0\\ 0&\text{for }t<0.\end{cases} (5)

where \phi(t) denotes an experimental relaxation function (such as e.g. the electrical polarization in dielectric experiments) normalized by the isothermal susceptibility \phi(0)=\chi _{0}-\chi _{\infty}. [1.2.2.3] Recall now the well known Laplace transform [9]

{\mathcal{L}}\left\{\exp(-\sqrt{t})\right\}(u)=\frac{1}{u}-\frac{\sqrt{\pi}}{2}u^{{-3/2}}\exp\left(\frac{1}{4u}\right)erfc\left(\frac{1}{2\sqrt{u}}\right) (6)

[page 2, §0]   where

erfc(x)=\frac{2}{\sqrt{\pi}}\int _{x}^{\infty}\exp(-y^{2})\mbox{\rm d}y (7)

denotes the complementary error function. [2.1.0.1] Inserting this into equation (2) and restoring {\tau _{{\beta}}} yields the known result[3]

\widehat{\chi}(u)=\frac{1}{2}\sqrt{\frac{\pi}{u{\tau _{{\beta}}}}}\exp\left(\frac{1}{4u{\tau _{{\beta}}}}\right)erfc\left(\frac{1}{2\sqrt{u{\tau _{{\beta}}}}}\right) (8)

for the complex susceptibility. [2.1.0.2] According to [7] there are no other cases of {\beta}\neq 1 for which an analytical expression is known for the Kohlrausch susceptibility. [2.1.0.3] My objectives in this paper are (i) to provide analytical expressions for the Kohlrausch susceptibility in the frequency domain in terms of H-functions for all {\beta}, (ii) to derive analytical expressions for the Davidson-Cole, Cole-Cole and Havriliak-Negami relaxation functions in the time domain, and (iii) to show that the approximate correspondence between Kohlrausch and Havriliak-Negami expressions in [7] is limited to a narrow frequency range.

[2.1.1.1] The objectives of this paper are achieved by employing a method based on so called H-functions [10]. [2.1.1.2] The H-function of order (m,n,p,q)\in{\mathbb{N}}^{4} and with parameters A_{i}\in{\mathbb{R}}_{+}(i=1,\ldots,p), B_{i}\in{\mathbb{R}}_{+}(i=1,\ldots,q), a_{i}\in{\mathbb{N}}(i=1,\ldots,p), and b_{i}\in{\mathbb{N}}(i=1,\ldots,q) is defined for z\in{\mathbb{N}},z\neq 0 by the contour integral [10, 11]

H^{{m,n}}_{{p,q}}\left(z\left|\begin{array}[]{l}{(a_{1},A_{1}),\ldots,(a_{p},A_{p})}\\ {(b_{1},B_{1}),\ldots,(b_{q},B_{q})}\end{array}\right.\right)=\frac{1}{2\pi i}\int _{{\mathcal{L}}}\eta(s)z^{{-s}}\;\mbox{\rm d}s (9)

where the integrand is

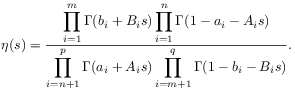\eta(s)=\frac{\displaystyle\prod _{{i=1}}^{m}\Gamma(b_{i}+B_{i}s)\prod _{{i=1}}^{n}\Gamma(1-a_{i}-A_{i}s)}{\displaystyle\prod _{{i=n+1}}^{p}\Gamma(a_{i}+A_{i}s)\prod _{{i=m+1}}^{q}\Gamma(1-b_{i}-B_{i}s)}. (10)

In (9) z^{{-s}}=\exp\{-s\log|z|-i\arg z\} and \arg z is not necessarily the principal value. [2.1.1.3] The integers m,n,p,q must satisfy

0\leq m\leq q,\qquad 0\leq n\leq p, (11)

and empty products are interpreted as being unity. [2.1.1.4] For the conditions on the other parameters and the path of integration the reader is referred to the literature [10] (see [12, p. 120ff] for a brief summary). [2.1.1.5] The importance of these functions for the present purpose arises from the facts that (i) they contain most special functions of mathematical physics as special cases and (ii) their Laplace transform is again an H-function. [2.2.0.1] Moreover they possess series expansions that are generalizations of hypergeometric series.

[2.2.1.1] Based on the convenient properties of H-functions the first objective can now be tackled. [2.2.1.2] An analytical expression for the Laplace transform of the Kohlrausch function is obtained as

{\mathcal{L}}\left\{\exp(-(t/{\tau _{{\beta}}})^{{\beta}})\right\}(u)=H^{{11}}_{{11}}\left(u^{{-{\beta}}}\left|\begin{array}[]{l}{(1,{\beta})}\\ {(1/{\beta},1)}\end{array}\right.\right). (12)

[2.2.1.3] The result is readily obtained from calculating formally

\displaystyle{\mathcal{L}}\left\{ H^{{m,n}}_{{p,q}}(z)\right\}(u)=\frac{1}{2\pi i}\int _{0}^{\infty}\int _{{\mathcal{L}}}\eta(s)e^{{-uz}}z^{{-s}}\;\mbox{\rm d}s\;\mbox{\rm d}z \displaystyle=\frac{1}{2\pi i}\int _{{\mathcal{L}}}\eta(s)u^{{s-1}}\Gamma(1-s)\;\mbox{\rm d}s
\displaystyle=\frac{1}{u}H^{{m,n+1}}_{{p+1,q}}\left(\frac{1}{u}\left|\begin{array}[]{l}{(0,1)(a_{1},A_{1}),\ldots,(a_{p},A_{p})}\\ {(b_{1},B_{1}),\ldots,(b_{q},B_{q})}\end{array}\right.\right) (13)

using the identification

\exp(-(t/{\tau _{{\beta}}})^{{\beta}})=H^{{10}}_{{01}}\left(\left(\frac{t}{{\tau}}\right)^{{\beta}}\left|\begin{array}[]{l}{-}\\ {(0,1)}\end{array}\right.\right), (14)

and then employing identities among H-functions [11, 12]. [2.2.1.4] Equation (12) answers the question raised in Reference [7] concerning existence of an analytical expression. [2.2.1.5] It will be seen that H-functions are not more difficult to compute than other transcendental functions. [2.2.1.6] Inserting equation (12) into (2) leads after some transformations involving H-function identities to the Kohlrausch susceptibility in the simple form

\widehat{\chi}(u)=1-H^{{11}}_{{11}}\left((u{\tau _{{\beta}}})^{{\beta}}\left|\begin{array}[]{l}{(1,1)}\\ {(1,{\beta})}\end{array}\right.\right). (15)

[2.2.1.7] This analytical result reduces the calculation of the Kohlrausch susceptibility to a Mellin-Barnes integral of the form (9).

[2.2.2.1] For practical purposes it is also of interest to have series expansions for the analytical results. [2.2.2.2] A Taylor series expansion can be obtained from equation (9) using the calculus of residues. [2.2.2.3] It reads for the H^{{11}}_{{11}}-function

H^{{11}}_{{11}}\left(z\left|\begin{array}[]{l}{(a,A)}\\ {(b,B)}\end{array}\right.\right)=\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(b+(1-a+k)B/A)}{A\Gamma(k+1)}z^{{-(1-a+k)/A}} (16)

[page 3, §0]   for B-A\leq 0. [3.1.0.1] Using this result the Kohlrausch susceptibility is found to have the series expansion (for |u{\tau _{{\beta}}}|>0)

\widehat{\chi}(u)=1-\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma({\beta}k+1)}{\Gamma(k+1)}(u{\tau _{{\beta}}})^{{-{\beta}k}} (17)

which reduces its computation to elementary additions and multiplications. [3.1.0.2] The result agrees with a direct evaluation of the Laplace transform of the series expansion for the stretched exponential function. [3.1.0.3] Finally, the asymptotic expansion

\widehat{\chi}(u)=1-\frac{1}{{\beta}}\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma((k+1)/{\beta})}{\Gamma(k+1)}(u{\tau _{{\beta}}})^{{k+1}} (18)

holds for |u{\tau _{{\beta}}}|\to 0. [3.1.0.4] It shows that the imaginary part increases linearly at low frequencies similar to the Cole-Davidson susceptibility.

[3.1.1.1] Using the method of H-functions sketched above allows also to find analytical expressions for the relaxation functions corresponding to stretched susceptibilities. [3.1.1.2] The results are summarized in the two tables below. Table 1 gives all relaxation functions, their H-function representations and their power series expansions, while Table 2 summarizes the susceptibilities in the frequency domain, their H-function representations and their power series expansions. [3.2.0.1] In these tables the notation

\Gamma(a,x)=\int _{a}^{\infty}y^{{a-1}}e^{{-y}}\mbox{\rm d}y (19)

denotes the complementary incomplete Gamma function, and the abbreviation

E_{a}(x)=\sum _{{k=0}}^{\infty}\frac{x^{k}}{\Gamma(ak+1)} (20)

is the Mittag-Leffler function. In addition the short hand notation

H_{a}(x)=H^{{11}}_{{11}}\left(-x\left|\begin{array}[]{l}{(1,1)}\\ {(1,a)}\end{array}\right.\right) (21)

was introduced for writing the Kohlrausch susceptibility.

Table 1: Normalized relaxation functions (f(0)=1) with relaxation time \tau. Series expansions in the rightmost column are asymptotic series whenever the range of validity of a series expansion is given as a limit.
f(t) H-function series
Debye \exp(-t/{\tau}) \displaystyle H^{{10}}_{{01}}\left(\frac{t}{{\tau}}\left|\begin{array}[]{l}{-}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}}{\Gamma(k+1)}\left(\frac{t}{{\tau}}\right)^{k}\\ \exp(-t/{\tau})\\ \end{array} \begin{array}[]{r}\displaystyle\frac{t}{{\tau}}<\infty\\ \\ \displaystyle\frac{t}{{\tau}}\to\infty\end{array}
Kohlrausch \exp(-(t/{\tau _{{\beta}}})^{{\beta}}) \displaystyle H^{{10}}_{{01}}\left(\left(\frac{t}{{\tau}}\right)^{{\beta}}\left|\begin{array}[]{l}{-}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}}{\Gamma(k+1)}\left(\frac{t}{{\tau _{{\beta}}}}\right)^{{{\beta}k}}\\ \exp(-(t/{\tau _{{\beta}}})^{{\beta}})\end{array} \begin{array}[]{r}\displaystyle\frac{t}{{\tau _{{\beta}}}}<\infty\\ \\ \displaystyle\frac{t}{{\tau _{{\beta}}}}\to\infty\end{array}
Cole-Cole E_{{\alpha}}(-(t/{\tau _{{\alpha}}})^{{\alpha}}) \displaystyle H^{{11}}_{{12}}\left(\left(\frac{t}{{\tau _{{\alpha}}}}\right)^{{\alpha}}\left|\begin{array}[]{l}{(0,1)}\\ {(0,1)(0,{\alpha})}\end{array}\right.\right) \begin{array}[]{cr}\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}}{\Gamma({\alpha}k+1)}\left(\frac{t}{{\tau}}\right)^{{{\alpha}k}}\\ \displaystyle\sum _{{k=1}}^{\infty}\frac{(-1)^{{k+1}}}{\Gamma(1-{\alpha}k)}\left(\frac{t}{{\tau _{{\alpha}}}}\right)^{{-{\alpha}k}}\end{array} \begin{array}[]{r}\displaystyle\frac{t}{{\tau _{{\alpha}}}}<\infty\\ \\ \displaystyle\frac{t}{{\tau _{{\alpha}}}}\to\infty\end{array}
Cole-Davidson \displaystyle\frac{\Gamma({\gamma},t/{\tau _{{\gamma}}})}{\Gamma({\gamma})} 1-\displaystyle\frac{1}{\Gamma({\gamma})}H^{{11}}_{{12}}\left(\frac{t}{{\tau _{{\gamma}}}}\left|\begin{array}[]{l}{(1,1)}\\ {({\gamma},1)(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle 1-\frac{1}{\Gamma({\gamma})}\sum _{{k=0}}^{\infty}\frac{(-1)^{k}}{(k+{\gamma})\Gamma(k+1)}\left(\frac{t}{{\tau _{{\gamma}}}}\right)^{{k+{\gamma}}}\\ \displaystyle\frac{\exp(-t/{\tau _{{\gamma}}})}{\Gamma({\gamma})}\left(\frac{t}{{\tau _{{\gamma}}}}\right)^{{{\gamma}-1}}\left[1+\sum _{{k=0}}^{\infty}\prod _{{j=1}}^{k}({\gamma}-j)\left[\frac{t}{{\tau _{{\gamma}}}}\right]^{{-k}}\right]\end{array} \begin{array}[]{r}\displaystyle\frac{t}{{\tau _{{\gamma}}}}<\infty\\ \\ \displaystyle\frac{t}{{\tau _{{\gamma}}}}\to\infty\end{array}
Havriliak-Negami \begin{array}[]{c}1-\displaystyle\frac{1}{\Gamma({\gamma})}H^{{11}}_{{12}}\left(\left[\frac{t}{{\tau _{{H}}}}\right]^{{\alpha}}\left|\begin{array}[]{l}{(1,1)}\\ {({\gamma},1)(0,{\alpha})}\end{array}\right.\right)\\ {\alpha}\neq 1\end{array} \begin{array}[]{c}\displaystyle 1-\frac{1}{\Gamma({\gamma})}\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(k+{\gamma})}{\Gamma({\alpha}k+{\alpha}{\gamma}+1)\Gamma(k+1)}\left[\frac{t}{{\tau _{{H}}}}\right]^{{{\alpha}(k+{\gamma})}}\\ \displaystyle\frac{1}{\Gamma({\gamma})}\sum _{{k=1}}^{\infty}\frac{(-1)^{{k+1}}\Gamma(k+{\gamma})}{\Gamma(1-{\alpha}k)\Gamma(k+1)}\left(\frac{t}{{\tau _{{H}}}}\right)^{{-{\alpha}k}}\end{array} \begin{array}[]{r}\displaystyle\frac{t}{{\tau _{{H}}}}<\infty\\ \\ \displaystyle\frac{t}{{\tau _{{H}}}}\to\infty\end{array}
Table 2: Normalized frequency dependent complex susceptibilities (u=-\mbox{i}\omega). Series expansions in the rightmost column are asymptotic series whenever the range of validity of a series expansion is given as a limit.
\widehat{\chi}(u) H-function series
Debye \displaystyle\frac{1}{1+u{\tau}} \displaystyle H^{{11}}_{{11}}\left(u{\tau}\left|\begin{array}[]{l}{(0,1)}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}(-1)^{k}(u{\tau})^{{-k-1}}\\ \displaystyle\sum _{{k=0}}^{\infty}(-1)^{k}(u{\tau})^{k}\\ \end{array} \begin{array}[]{r}|u{\tau}|>1\\ \\ |u{\tau}|<1\end{array}
Kohlrausch 1-H_{{\beta}}(-(u{\tau _{{\beta}}})^{{\beta}}) \displaystyle 1-H^{{11}}_{{11}}\left((u{\tau _{{\beta}}})^{{\beta}}\left|\begin{array}[]{l}{(1,1)}\\ {(1,{\beta})}\end{array}\right.\right) \begin{array}[]{c}\displaystyle 1-\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma((k+1)/{\beta})}{{\beta}\Gamma(k+1)}(u{\tau _{{\beta}}})^{{k+1}}\\ \displaystyle 1-\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma({\beta}k+1)}{\Gamma(k+1)}(u{\tau _{{\beta}}})^{{-{\beta}k}}\\ \end{array} \begin{array}[]{r}|u{\tau _{{\beta}}}|\to 0\\ \\ |u{\tau _{{\beta}}}|>0\end{array}
Cole-Cole \displaystyle\frac{1}{1+(u{\tau _{{\alpha}}})^{{\alpha}}} \displaystyle H^{{11}}_{{11}}\left((u{\tau _{{\alpha}}})^{{\alpha}}\left|\begin{array}[]{l}{(0,1)}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}(-1)^{k}(u{\tau _{{\alpha}}})^{{{\alpha}k}}\\ -\displaystyle\sum _{{k=0}}^{\infty}(-1)^{k}(u{\tau _{{\alpha}}})^{{-{\alpha}(k+1)}}\\ \end{array} \begin{array}[]{r}|u{\tau _{{\alpha}}}|<1\\ \\ |u{\tau _{{\alpha}}}|>1\end{array}
ColeDavidson \displaystyle\frac{1}{(1+u{\tau _{{\gamma}}})^{{\gamma}}} \displaystyle\frac{1}{\Gamma({\gamma})}H^{{11}}_{{11}}\left(u{\tau _{{\gamma}}}\left|\begin{array}[]{l}{(1-{\gamma},1)}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(k+{\gamma})}{\Gamma({\gamma})\Gamma(k+1)}(u{\tau _{{\gamma}}})^{k}\\ -\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(k+{\gamma})}{\Gamma({\gamma})\Gamma(k+1)}(u{\tau _{{\gamma}}})^{{-(k+{\gamma})}}\\ \end{array} \begin{array}[]{r}|u{\tau _{{\gamma}}}|<1\\ \\ |u{\tau _{{\gamma}}}|>1\end{array}
Havriliak-Negami \displaystyle\frac{1}{(1+(u{\tau _{{H}}})^{{\alpha}})^{{\gamma}}} \displaystyle\frac{1}{\Gamma({\gamma})}H^{{11}}_{{11}}\left((u{\tau _{{H}}})^{{\alpha}}\left|\begin{array}[]{l}{(1-{\gamma},1)}\\ {(0,1)}\end{array}\right.\right) \begin{array}[]{c}\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(k+{\gamma})}{\Gamma({\gamma})\Gamma(k+1)}(u{\tau _{{H}}})^{{{\alpha}k}}\\ -\displaystyle\sum _{{k=0}}^{\infty}\frac{(-1)^{k}\Gamma(k+{\gamma})}{\Gamma({\gamma})\Gamma(k+1)}(u{\tau _{{H}}})^{{-{\alpha}(k+{\gamma})}}\\ \end{array} \begin{array}[]{r}|u{\tau _{{H}}}|<1\\ \\ |u{\tau _{{H}}}|>1\end{array}

[page 4, §1][4.1.1.1] Having computable analytical expressions at hand for the Kohlrausch susceptibility it becomes possible to investigate the mappings between the Kohlrausch susceptibility and the Havriliak-Negami susceptibility [6]

\widehat{\chi}(u)=\frac{1}{(1+(u{\tau _{{H}}})^{{\alpha}})^{{\gamma}}} (22)

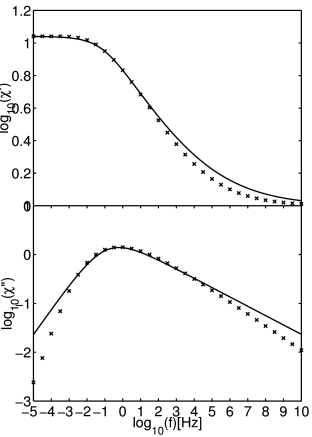
that were postulated in Ref. [7]. [4.1.1.2] Table I and Figure 5 in Ref. [7] present fits for the Kohlrausch susceptibility using the Havriliak-Negami expression as fit function. [4.1.1.3] Figure 1 shows real and imaginary part of the Kohlrausch susceptibility with {\beta}=0.25 plotted as crosses (\times) in a doubly logarithmic plot. [4.1.1.4] The corresponding Havriliak-Negami fit from [7] with {\alpha}=0.5164, {\gamma}=0.3706 and {\tau _{{H}}}/{\tau _{{\beta}}}=10 is shown as the solid line. In all calculations \chi _{\infty}=1 and \chi _{0}=10 unless stated otherwise.

Figure 1: Comparison of the Havrialiak-Negami fit (solid line) with {\alpha}=0.5164, {\gamma}=0.3706 and {\tau _{{H}}}=10 for a Kohlrausch susceptibility (\times) with {\beta}=0.25 and {\tau _{{\beta}}}=1. The values were taken from Ref. [7], page 7310, Table I. In all cases \chi _{\infty}=1 and \chi _{0}=10.

[4.1.2.1] Because it is known that the phenomenological susceptibility functions are often inadequate for fitting experimental relaxation spectra, some researchers prefer not to discuss stretching exponents but the width of the imaginary part [13]. [4.1.2.2] Figure 2 plots three characteristic frequencies for all three stretched susceptibility functions against their respective stretching exponent. [4.2.0.1] The first is f_{0}, the location of the maximum of the imaginary part. [4.2.0.2] The second is f_{-}, the location of the lower half width point of the imaginary part. [4.2.0.3] The third is f_{+}, the location of the upper half width point of the imaginary part. [4.2.0.4] The half width points are defined as the frequencies at which the imaginary part has decayed to half of its maximum value.

Figure 2: Location of the frequency of the maximum f_{0}, frequency f_{-} of lower half width and frequency f_{+} of upper half width of the imaginary part of Cole-Cole, Kohlrausch and Cole-Davidson susceptibility functions as function of the respective stretching exponents {\alpha}, {\beta}, {\gamma}. The upper and lower half width frequencies f_{\pm} are indicated by solid lines connected with symbols (Cole-Cole susceptibility function (\triangle), Kohlrausch susceptibility (\circ), Cole-Davidson (\Box)). The location of the maximum of the imaginary part is indicated by a dashed line for the Cole-Cole function, by a solid line without symbols for the Kohlrausch function and by a dashdotted line for the Cole-Davidson function. The relaxation time is always \tau=1.

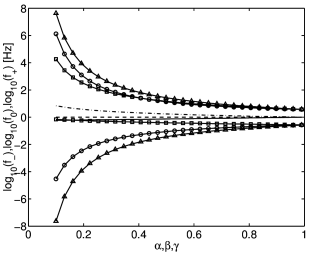
[4.2.1.1] Figure 2 shows that while the Cole-Cole susceptibility (dashed line for maximum, solid line with triangles for the half widths) is symmetric the other two susceptibilities are asymmetric. [4.2.1.2] For small values of {\beta} resp. {\gamma} the Cole-Davidson is more strongly asymmetric than the Kohlrausch susceptibility. [4.2.1.3] Note also that the lower halfwidth point moves to higher frequencies for diminishing {\gamma} in the Cole-Davidson case. [4.2.1.4] The total width of the relaxation peak in decades is the difference between the upper and the lower half width. [4.2.1.5] For {\alpha}={\beta}={\gamma}=0.2 the total width of the Cole-Cole function is roughly 7 decades, the width of the Kohlrausch susceptibility is roughly 5 decades, and that of the Cole-Davidson is roughly 2.5 decades. [4.2.1.6] Figures 2 and 1 demonstrate that the mapping between the Kohlrausch parameter {\beta} and the Cole-Davidson parameter {\gamma} that is often employed by practitioners [2] becomes increasingly inaccurate for small values of the stretching exponents.

[page 5, §1][5.1.1.1] In summary the present paper has given unified representations of nonexponential relaxation and non-Debye susceptibilities in terms of H-functions. [5.1.1.2] These representations lead to computable expressions that were used to investigate the relations between the Kohlrausch susceptibility and other fit functions. [5.2.0.1] The H-function representations given here can help to facilitate the computational transformation between the frequency and time domain in theoretical considerations and experiment.