4.1 Hydrostatic equilibrium
[5.0.1.1] The constitutive theory proposed above, contrary to the
traditional theory, does not postulate a unique
capillary pressure as a constitutive parameter function.
[5.0.1.2] On the other hand experimental evidence suggests that
capillary pressure is a useful concept to correlate
observations.
[5.0.1.3] To make contact with the established traditional theory
it is therefore important to check
whether the traditional
PcSW relation
can be viewed as a derived concept within the new theory.
[5.0.2.1] Consider first the case of hydrostatic equilibrium
where vi=0 for all i=1,2,3,4.
[5.0.2.2] In hydrostatic equilibrium all fluids are at rest.
[5.0.2.3] In this case the traditional theory implies
∂SW/∂t=0 and ∂SO/∂t=0,
by mass balance eq. (11).
[5.0.2.4] The traditional momentum balance
eqs. (12) can be integrated to give
| PWx | =PWx0+ϱWg⋅x-x0 |
| (31a) |
| POx | =POx0+ϱOg⋅x-x0 |
| (31b) |
where x0 is a point in the boundary.
[5.0.2.5] Combined with the assumption (13) one finds
| PcSWx | =POx-PWx |
| (32) |
| =Pc0+ϱO-ϱWg⋅x-x0 |
|
implying the existence of a unique
hydrostatic saturation profile SWx.
[5.0.2.6] Here Pc0=Pcx0 is the capillary pressure at x=x0.
[5.0.2.7] Experiments show, however, that hydrostatic saturation profiles
are not unique.
[5.0.2.8] As a consequence the traditional theory employs
multiple PcSW relations for drainage and
imbibition, and this leads to difficult problems
when imbibition and drainage occur simultaneously.
[5.0.3.1] The nonlinear theory proposed here can be solved in the
special case of hydrostatic equilibrium.
[5.0.3.2] Mass balance (1) now implies
∂Si/∂t=0 for all i=1,2,3,4.
[5.0.3.3] Integrating eqs. (2) yields
| P1x | =P1x0+ϱWg⋅x-x0 |
| (33a) |
| P3x | =P3x0+ΠaS1x-α-S1x0-α |
| (33b) |
| +γP2*S2xγ-1-S2x0γ-1 |
|
| +ϱWg⋅x-x0 |
|
| P3x | =P3x0+ϱOg⋅x-x0 |
| (33c) |
| P1x | =P1x0+ΠbS3x-β-S3x0-β |
| (33d) |
| +δP4*S4xδ-1-S4x0δ-1 |
|
| +ϱOg⋅x-x0 |
|
If one identifies P1 with PW and P3 with PO then
eqs. (33a)
and (33b) suggest to identify
Pc as P3-P1.
[5.1.0.1] Then eqs. (33c) and (33d)
combined with
S1=SW-S2 and S3=1-SW-S4 imply
Pc=PcSW,S2,S4.
[5.1.0.2] The capillary pressure Pc depends not only
on SW but also on S2 and S4
in hydrostatic equilibrium.
[5.1.0.3] In the theory proposed here it is not possible to identify
a unique PcSW relation when all fluids are at rest.
This agrees with experiment.
4.2 Residual decoupling approximation
[5.1.1.1]
While it is not possible to identify a unique PcSW
relation in hydrostatic equilibrium such a functional relation
emerges nevertheless from the present theory when the
system approaches hydrostatic equilibrium
in the residual decoupling approximation.
[5.1.1.2] The approach to hydrostatic equilibrium in
the residual decoupling approximation (RDA)
can be formulated mathematically
as v4=0,v2=0 and R23=0,R41=0.
[5.1.1.3] In addition it is assumed that the velocities v1,v3→0
are small but nonzero.
[5.1.1.4] In the RDA mass balance becomes
| ∂S1∂t | +∇⋅S1v1=η2S2-S2*SW*-SW∂SW∂t |
| (34a) |
| ∂S2∂t | =-η2S2-S2*SW*-SW∂SW∂t |
| (34b) |
| ∂S3∂t | +∇⋅S3v3=η4S4-S4*SO*-SO∂SO∂t |
| (34c) |
| ∂S4∂t | =-η4S4-S4*SO*-SO∂SO∂t |
| (34d) |
Momentum balance becomes in the RDA
| ϕ1∇P1-ϱWg=R13v3-R1+M1v1 |
| (35a) |
| 0=ϕ2∇P3+∇ΠcW-γP2*∇S2γ-1-ϱWg |
| (35b) |
| ϕ3∇P3-ϱOg=R31v1-R3+M3v3 |
| (35c) |
| 0=ϕ4∇P1+∇ΠcO-δP4*∇S4δ-1-ϱOg |
| (35d) |
where the abbreviations
| R1 | =R13+R14+R15 |
| (36a) |
| R3 | =R31+R32+R35 |
| (36b) |
were used.
[5.1.1.5] Equations (34) and (35)
together with eq.(16b) provide
17 equations for 12 variables (P1,P3,v1,v3
and Si,i=1,2,3,4).
[5.1.2.1] Equations (34) and (35)
can now be compared to the traditional equations
(11)–(13) with the aim
of identifying capillary pressure and relative
permeability.
[5.1.2.2] Consider first the momentum balance eqs. (35).
[5.1.2.3] As in the traditional theory [24] viscous decoupling
is assumed to hold, i.e. R31=0 and R13=0.
[5.1.2.4] Next, assuming that
R1≫M1, R3≫M3, and Si≠0
one finds
[page 6, §0]
| ϕ1∇P1-ϱWg=-R1v1=-R1ϕWϕ1vW |
| (37a) |
| ∇P3=-∇ΠcW+γP2*∇S2γ-1+ϱWg |
| (37b) |
| ϕ3∇P3-ϱOg=-R3v3=-R3ϕOϕ3vO |
| (37c) |
| ∇P1=-∇ΠcO+δP4*∇S4δ-1+ϱOg |
| (37d) |
where barycentric velocities
vW,vO defined through
| SWvW | =S1v1+S2v2 |
| (38a) |
| SOvO | =S3v3+S4v4 |
| (38b) |
have been introduced.
[6.0.0.1] Subtracting eq. (37a) from eq. (37c),
as well as eq. (37d) from eq. (37b),
and equating the result gives
| 2ϱO-ϱWg+R1ϕ12ϕWvW-R3ϕ32ϕOvO= |
|
| ∇ΠaS1-α-ΠbS3-β+γP2*S2γ-1-δP4*S4δ-1 |
| (39) |
where eq. (22) has also been employed.
[6.0.0.2] This result can be compared to the traditional theory
where one finds from eqs. (12) and (13)
| ϱO-ϱWg+μWkkWrϕWvW-μOkkOrϕOvO=∇Pc |
| (40) |
Again this seems to imply Pc=PcSW,S2,S4
as already found above for hydrostatic equilibrium.
[6.0.0.3] However, within the RDA additional constraints follow
from mass balance (34).
[6.0.1.1] First, observe that
adding (34a) to (34b)
resp. (34c) to (34d)
with the help of eq. (38a)
yields the traditional mass balance eqs. (11).
[6.0.1.2] Next, verify by insertion that eqs. (34b)
and (34d) admit the solutions
| S2x,t | =S2*x+S20x-S2*x |
| (41a) |
| ×(SW*x-SWx,tSW*x-SW0x)η2 |
|
| S4x,t | =S4*x+S40x-S4*x |
| (41b) |
| ×(SWx,t-SW*xSW0x-SW*x)η4 |
|
where the displacement process is assumed to start from
the initial conditions
| SWx,t0 | =SW0x |
| (42a) |
| S2x,t0 | =S20x |
| (42b) |
| S4x,t0 | =S40x |
| (42c) |
at some initial instant t0.
[6.1.0.1] The limiting saturations SW*, SO*, S2*,S4*
are given by eqs. (29).
[6.1.0.2] They depend only on the sign of
∂SW/∂t if
τ≫∂SW/∂t can be assumed to hold.
[6.1.0.3] One finds in this case
| SW* | =1-SOim |
| (43a) |
| SO* | =SOim |
| (43b) |
| S2* | =0 |
| (43c) |
| S4* | =SOim |
| (43d) |
for imbibition processes (i.e. ∂SW/∂t>0), resp.
| SW* | =SWdr |
| (44a) |
| SO* | =1-SWdr |
| (44b) |
| S2* | =SWdr |
| (44c) |
| S4* | =0 |
| (44d) |
for drainage processes (i.e. ∂SW/∂t<0).
[6.1.1.1] With these solutions in hand
the capillary pressure can
be identified up to a constant as
| Pc(SW)=12[Πa(SW-S2)-α |
| (45) |
| -Πb(1-SW-S4)-β+γP2*S2γ-1-δP4*S4δ-1] |
|
where S2=S2SW and S4=S4SW
are given by eqs. (41).
[6.1.1.2] This result holds in the RDA combined with
the assumptions above.
[6.1.1.3] Furthermore, equations (37a) and (37c)
are recognized as generalized Darcy laws with relative permeabilities
identified as
| kWrSW | =2R1-1μWkϕ2SW-S22 |
| (46a) |
| kOrSW | =2R3-1μOkϕ21-SW-S42 |
| (46b) |
where S2=S2SW and S4=S4SW
are again given by eqs. (41).
4.3 Reproduction of experimental observations
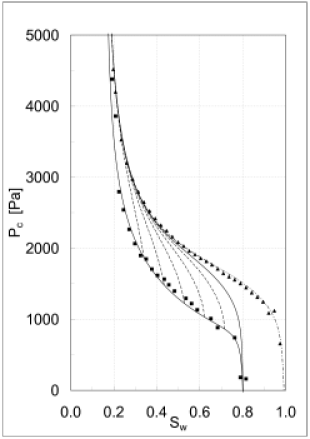
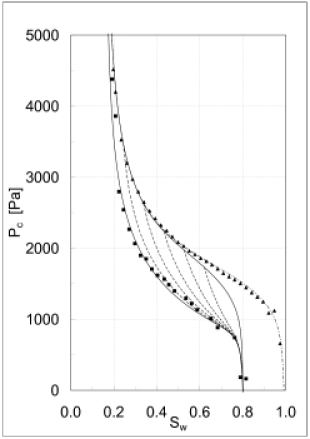
[6.1.2.1] Figure 1 visualizes the results obtained by fitting
eq. (45) to experiment.
[6.1.2.2] The experimental results are depicted as
triangles (primary drainage) and squares (imbibition).
[6.1.2.3] The experiments were performed in a medium grained
unconsolidated water wet sand of porosity ϕ=0.34.
[6.1.2.4] Water was used as wetting fluid while air
resp. TCE were used as the nonwetting fluid.
[6.1.2.5] The experiments were carried out over a period of
several weeks at the Versuchseinrichtung zur Grundwasser-
und Altlastensanierung (VEGAS)
[page 7, §0] at the Universität Stuttgart.
[7.0.0.1] They are described in more detail in Ref. [25].
The parameters for all the curves shown in all four
figures are
SWdr=0.15,
SOim=0.19,
α=0.52,
β=0.90,
γ=1.5,
δ=3.5
η2=4,
η4=3,
Πa=1620 Pa,
Πb=25 Pa, and
P2*=2500 Pa
P4*=400 Pa.
[7.0.1.1] If it is further assumed that the medium is isotropic and
that the matrices R1,R3 have the form
| R1 | =R1*ϕ1-κW1 |
| (47a) |
| R3 | =R3*ϕ3-κO1 |
| (47b) |
then the relative permeability functions are
obtained from eqs. (46).
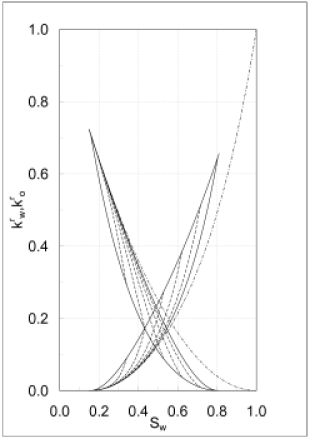
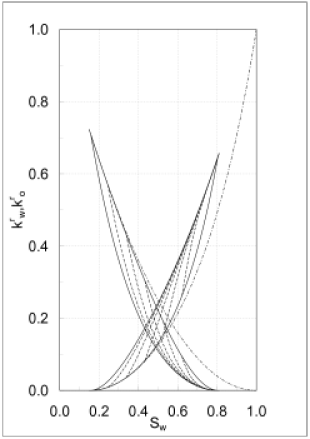
[7.0.1.2] The result for the special case κW=κO=0 is shown
in Figures 3 and 4.
[7.0.1.3] The parameters R1*,R3*
are chosen such that R1*=2ϕ2μW/k and
R3*=2ϕ2μO/k,
where μW,μO are the fluid viscosities
and k is the absolute permeability of the medium.
[7.0.1.4] All other parameters for the relative permeability
functions shown in Figures 3 and 4
are identical to those of the capillary pressure curves
in Figures 1 and 2.
[7.0.2.1] Note that Figures 1 through 4 show
a total of 30 different scanning curves, 5 drainage
and 5 imbibition scanning curves each for
Pc,kWr and kOr.
[7.1.0.1] In addition a total of 9 different bounding curves
are displayed, namely
the primary drainage, secondary drainage and
secondary imbibition curve for Pc,kWr and kOr.
[7.1.0.2] Three more bounding curves namely primary imbibition
for Pc,kWr and kOr starting from SW=0
are not shown because they are difficult to obtain
experimentally for a water-wet sample.
[7.1.0.3] Of course the number of scanning curves
can be increased indefinitely.
[7.1.0.4] All of these curves have the same
values of the constitutive parameters.
[7.1.0.5] There is less than one parameter per curve.
[7.1.0.6] The curves shown in the figures exhibit the full range
of hysteretic phenomena known from experiment.
[7.1.0.7] Nevertheless it should be kept in mind that these
curves are obtained only under special approximations,
and when these are not valid such curves do not exist.