Article
[page 1, §1]
[1.1.1.1] Accurate prediction and understanding
of material parameters for
disordered systems such as rocks [1],
soils [2], papers [3], clays [4],
ceramics [5], composites [6], microemulsions [7]
or complex fluids
require geometrical microstructures as a starting point
as emphasized by Landauer [8] and numerous authors
[9, 10, 11, 12].
[1.1.1.2] Digital three dimensional images of unprecedented
size and accuracy have been prepared for the case
of Fontainebleau sandstone,
and are being made available to the scientific
community in this brief report.
[1.1.2.1] Multiscale modelling of disordered media
has recently become a research focus in mathematics
and physics of complex materials and
porous media [13, 14, 15, 16, 17, 18].
[1.1.2.2] Accurate prediction of physical observables
for multiscale heterogeneous media
is a perennial problem [9, 8].
[1.1.2.3] It requires knowledge
of the three dimensional disordered microstructure [11].
[1.1.2.4] Our objective in this brief report is to
provide to the scientific public a sequence of fully three dimensional
digital images with a realistic strongly correlated
microstructure typical for sandstone.
[1.1.2.5] Resolutions from
a=117.18μm
to
0.4576μm
are available for download
[19].
[1.1.2.6] Experimental computed microtomographic images
of comparable size, resolution or data quality are,
to the best of our knowledge, not available at present.
[1.1.2.7] More importantly,
experimental images of similar size and quality are not
expected to become available to the
scientific community in the near future.
[1.1.3.1] Despite the impressive progress in fully three dimensional
high resolution X-ray and synchrotron computed tomography
of porous media in recent years [20, 21]
acquisition times for 1500 radiograms needed for a
1024×1024×1024-sample of average quality
at the ID19 beamline
of the European Synchrostron Radiation Facility
are on the order of 30 minutes [22].
[1.1.3.2] Extrapolating to the number of 32768 such
blocks, that we provide in this report,
would thus require on the order of 16384 hours
or roughly 2 years of uninterrupted beamtime.
[1.1.3.3] It is unlikely that this amount of beamtime
will ever be spent.
[1.1.4.1] The continuum multiscale modeling technology for carbonates
developed in [23, 24, 25] was applied to Fontainebleau
sandstone in [26], to create
a synthetic, non-experimental image at very high resolution.
[1.2.0.1] A laboratory sized cubic sample of sidelength
1.8cm
was generated containing roughly
1.02×106
polyhedral quartz grains.
[1.2.0.2] For simplicity there are a total of 99 grain types
each defined by eighteen intersecting planes.
[1.2.0.3] The grains are rescaled, randomly oriented and
have a prescribed overlap with each other
(see [26] for more modeling details).
[1.2.0.4] The model was geometrically calibrated against a
well studied experimental
microtomogram at
7.5μm
resolution [27].
[1.2.0.5] The geometric calibration was based on
matching porosity, specific surface, integrated
mean curvature, Gaussian curvature, correlation function,
local porosity distributions (with
240μm
and
480μm
measurement cell size),
and local percolation probabilities at the same
measurement cell sizes.
[1.2.0.6] Comparison of these quantities
at
a=7.5μm
was carried out in [26].
[1.2.1.1] The continuum sample generated and characterized
in [26] is the starting point for the
work reported here.
[1.2.1.2] To eliminate boundary effects a centered cubic sample,
denoted by S,
of sidelength
1.5cm
was cropped from the original deposit.
[1.2.1.3] The pore space inside S is denoted by P,
the matrix region is denoted M.
[1.2.2.1] The sample region S was discretized into
N cubic voxels
Via⊂S (i=1,…,N), whose
sidelength a is a multiple of the base
resolution
a0=1.5cm/16384=0.9155273μm
.
[1.2.2.2] The discretization employs a cubic array
of 63=216 collocation points placed centrally
and distributed uniformly inside each voxel
Via.
[1.2.2.3] It yields an integer gray scale value
0≤gia≤216 with 1≤i≤N
for each of the N voxels (discrete
[page 2, §0]
volume elements).
[2.1.0.1] The gray value gia∈N equals the number
of collocation points inside voxel Vi,
that fall into the matrix region M [26].
The gray values approximate the integral
| ψia=1a3∫Vi∩Pd3x≈1-gia216, | | (1) |
which is the porosity inside the voxel Vi
at resolution a.
[2.1.0.2] Thus, gia=0 approximates Vi⊂P,
while gia=216 approximates Vi⊂M.
| a |
128a0 |
64a0 |
32a0 |
16a0 |
8a0 |
4a0 |
2a0 |
a0 |
a0/2 |
| L |
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
16384 |
32768 |
| N |
221 |
224 |
227 |
230 |
233 |
236 |
239 |
242 |
245 |
| K |
1 |
1 |
1 |
1 |
8 |
64 |
512 |
4096 |
32768 |
| TCPU [h] |
1.6 |
3.2 |
6.5 |
11 |
88 |
704 |
5632 |
45056 |
360448 |
Table 1:
Overview of data sets available from
http:www.icp.uni-stuttgart.demicroct for download.
a is the resolution in units of
a0=0.91552734μm
.
L is the sidelength of the cubic sample in units of aa0.
The total number of voxels is N, and
K is the number of cubic blocks used to represent
the sample. One has K>1 whenever L>1024.
TCPU gives an estimate of the total CPU time in hours,
that was used to generate the discretizations.
Calculations were typically performed in parallel
on 512 Xeon processors requiring a total wall
time of approximately Twall=TCPU/512 in hours
due to an essentially linear speedup.
Total wall time was around 800 hours or 34 days.
[2.1.1.1] At the lowest resolution
a=128a0=117.18μm
the sample consists of
N=128×128×128=2097152
discrete volume elements (voxels),
and it can easily be stored in a single file.
[2.1.1.2] At higher resolution this becomes technically
inconvenient, and we have limited the
file size to blocks with
1024×1024×1024=1073741824
voxels corresponding to roughly 1 Gigabyte.
[2.1.1.3] The highest resolution at which the sample
is still stored in a single file is
a=16a0=14.65μm
.
[2.1.1.4] For resolutions
a≤8a0=7.3244μm
the data
are stored in several blocks.
[2.1.1.5] This results in a maximum of
32768 blocks for the highest resolution of
a=a0/2=0.4576μm.
[2.1.1.6] The number of voxels is
N=245=35184372088832
at this resolution.
[2.1.1.7] Table 1 gives a summary of the available
resolutions a,
sample sidelength L (in units of a),
number of voxels N,
number of 10243-blocks K, and
an estimate of the CPU time and wall
time expended for the computation.
[2.1.2.1] All computations were performed on the
HLRS’s bwGRID cluster at the Universität Stuttgart
consisting of 498 compute nodes each holding two Intel Xeon CPU’s
capable of 11.32 GFLOPs.
[2.1.2.2] The peak performance (Linpack) is 38 TFLOP [28].
For the calculations performed in this work 256 nodes
(=512 CPU’s) were used in parallel.
[2.1.2.3] The discretization algorithm was parallelized,
but not optimized.
[2.1.2.4] Every discretized volume element (voxel) requires
one byte of storage.
[2.1.2.5] The storage requirements without compression
amount to roughly 40 Terabytes.
[2.1.3.1] The results can be used to calculate resolution
dependent geometric and physical properties.
[2.1.3.2] Because the underlying continuum microstructure
is available with floating point precision, the
resolution can be changed over many decades.
[2.1.3.3] Resolution dependent geometrical or
physical properties can be compared with,
or extrapolated to, the continuum result.
[2.1.3.4] This is illustrated with the porosity ϕ
(volume fraction of pore space)
and specific internal surface S
(surface area per unit volume).
[2.1.4.1] The exact values of ϕ and S
are not known for the continuum model.
[2.1.4.2] Depending on the geometrical or physical
quantity of interest computations on
the continuum model as well as computations
on discretizations with
more than 10243 discrete volume elements
are (as a rule) challenging at present.
[2.1.5.1] The discretized samples approximate
the exact geometry of the continuum
model.
[2.1.5.2] Let δij=1 for i=j and δij=0 for i≠j.
[2.2.0.1] Then
is the number of voxels with grey value g at
resolution a, and
| ϕgth,a=1N∑g=0gthMg,a | | (3) |
is an estimate for the porosity
based on a segmentation of its
discretization
at resolution a
with segmentation threshold gth.
[2.2.0.2] The porosity ϕ=lima→0ϕgth,a
of the continuum model at infinite resolution
is expected to obey
for all gth and all a.
[2.2.0.3] The validity of these bounds depends on
the continuum microstructure.
[2.2.0.4] They are expected to hold approximately
for the sandstone microstructure.
[2.2.0.5] Grey values g=0 and g=216
do not guarantee, that the pore boundary
does not intersect the voxel region,
although it will be true for the majority of voxels
in the limit a→0.
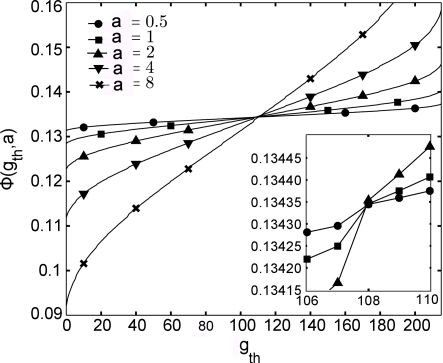
[2.2.1.1] Figure 1 shows the
porosity ϕgth,a as a function of
the segmentation threshold gth
for resolutions a=8a0,4a0,2a0,a0,a0/2.
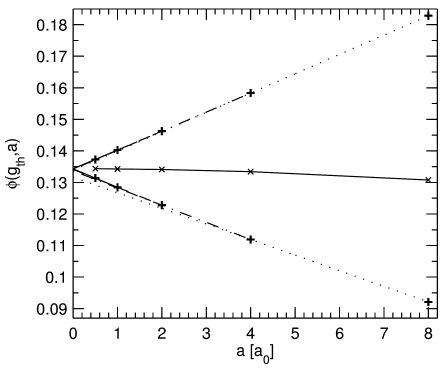
[2.2.2.1] Figure 2 shows the porosity
bounds ϕ0,a and ϕ215,a for
resolutions a=8a0,4a0,2a0,a0,a0/2.
[2.2.2.2] It also shows eight extrapolations defined as the linear functions
where i∈0,215 and the slopes kic and
intercepts φic are determined such that
for a=c and a=c/2.
[2.2.2.3] Table 2 lists the slopes and intercepts of all eight
extrapolations.
[2.2.2.4] In between the upper and lower bounds
Figure 2 also shows (with symbols × connected
by a solid line)
the porosity obtained by maximizing the variance
[page 3, §0]
of the grey scale histogram,
a standard technique in
image processing [29].
| c |
k0c |
φ0c |
k215c |
φ215c |
| 8a0 |
-0.004944104133756 |
0.131677153054625 |
0.006128869055829 |
0.133806445926894 |
| 4a0 |
-0.005437994277600 |
0.133652713629999 |
0.006038194581379 |
0.13416914382469 |
| 2a0 |
-0.005680456774371 |
0.134137638623542 |
0.005981708264244 |
0.134282116458962 |
| a0 |
-0.005843877976029 |
0.134301059825200 |
0.005942813391024 |
0.13432101133218 |
Table 2:
Slopes and intercepts for extrapolations in Figure
2 according to
equation (
5).
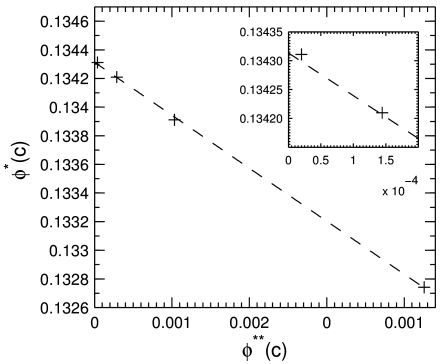
[3.1.1.1] Figure 3 shows the mean values
plotted against the differences
as data points.
[3.1.1.2] It also shows a linear fit to the data as a dashed line.
[3.1.1.3] The linear fit extrapolates to the value
| limc→0ϕ*c=0.134313±0.00001 | | (9) |
where the uncertainty is from the residues of the fit.
| aa0 |
8 |
4 |
2 |
1 |
0.5 |
| Smaxa [mm-1] |
20.039 |
20.530 |
20.774 |
20.904 |
20.946 |
| Smfa [mm-1] |
9.6371 |
9.8774 |
9.9978 |
10.061 |
10.065 |
| Smina [mm-1] |
6.0407 |
6.1915 |
6.2673 |
6.3068 |
6.3096 |
| Smeasureda [mm-1] |
9.168±0.02 |
9.825±0.06 |
10.159±0.16 |
10.307±0.43 |
10.355±1.34 |
Table 3: Smaxa and
Smina are the upper and
lower bounds computed from
eqs. (
16) resp. (
17) and eq. (
18)
for specific internal surfaces
as functions of resolution
a.
Smfa is the mean field estimate
computed from eqs. (
18)–(
23).
Smeasureda is calculated by applying
the direct algorithm from
[30]
to thresholded cubic subsamples, and
averaging the results as described in the last
paragraph of the main text.
[3.1.2.1] We now turn to an estimate for the specific internal surface S.
[3.1.2.2] Assume, that every voxel Via at resolution a
with 0<gia<216 is cut by a single plane.
[3.1.2.3] Let BiR denote a ball with radius R
centered at the center of the voxel Via.
[3.1.2.4] Then Bia/2 is the inscribed ball
with radius a/2, and
Bi3a/2 denotes the circumscribed ball
with radius 3a/2.
[3.1.2.5] If the voxel is cut by a single plane, then
the surface area of the cut is bounded above
by the area of the circle forming the base of the
spherical cap cut from the circumscribed ball
3a/2.
[3.1.2.6] Let b denote the radius of the circle
forming the base, let h denote
the height of the cap, and let R be the radius
of the sphere from which the cap is cut.
[3.2.0.1] Then
and
is the volume of the spherical cap.
[3.2.0.2] Introducing the voxel porosity
and solving the last equation for h and
gives
| hmψ=R1+2cosarccos1-2ψ+2mπ3 | | (13) |
as a function of voxel porosity, where m=0,1,2.
[3.2.0.3] The inequality
selects the
solution with m=2.
[3.2.0.4] The area of the circle at the base of the spherical cap
is A=πb2 so that
| Aψ,R=πh2ψ2R-h2ψ | | (15) |
is the relation between the circular base area and the
volume fraction of a spherical cap cut from a sphere of radius R.
[page 4, §0]
[4.1.0.1] Combined with eq. (1) this yields the
upper bound
| Smaxg,a=1a3A1-g216,3a2 | | (16) |
for the specific internal surface inside a voxel
with resolution a having grey value g
under the assumption that the voxel is cut by a
single flat plane.
[4.1.1.1] For the lower bound
we use the circular base area obtained by
the intersection with the inscribed ball
Bia/2 of radius a/2.
[4.1.1.2] The minimum is attained when the intersection
plane is oriented perpendicular to one of the space
diagonals of the cubic voxel.
[4.1.1.3] The inscribed ball is intersected by the plane only when its
distance from the nearest voxel corner exceeds a3-1/2.
[4.1.1.4] This occurs at
ψ=33-13/16≈0.042468 and at
ψ=1-33-13/16≈0.95753.
[4.1.1.5] Therefore, one finds the lower bound
Sming,a=0 for g≤9 and
g≥206, while
| Sming,a=1a3A1-g216,a2 | | (17) |
holds for 10≤g≤205.
[4.1.1.6] Upper and lower bounds for the specific surface
are obtained from these results by summation as
| Sba=1Na∑g=1215Mg,aSbg,a | | (18) |
where b=min resp. b=max.
[4.1.1.7] Table 3 lists the results for
Smina and Smaxa
for a=8a0,4a0,2a0,a0,a0/2.
[4.1.2.1] Table 3 shows that the bounds for the specific
surface are rather wide.
[4.1.2.2] It is then of interest to investigate the following
simple geometric estimate:
In the limit a→0
most voxels are intersected by a single plane.
[4.1.2.3] The intersecting planes can have varying orientations.
[4.1.2.4] As a simple approximation it may be assumed, that the
effect of different orientations is averaged out, and
that a single orientation suffices to estimate the
specific surface inside a voxel.
[4.1.2.5] Here we assume this single direction to be a space
diagonal of the voxel.
[4.1.2.6] All four space diagonals are equivalent by symmetry
so that it suffices to consider one direction.
[4.1.2.7] A simple meanfield like
appproximation is to assume,
that every voxel with porosity ψia
given in eq. (1) is intersected by a
single plane oriented perpendicular to one of the four
space diagonals of the voxel.
[4.1.3.1] Let 0≤d≤3a denote the distance from the corner of
the voxel along the diagonal to the intersection point,
where the plane intersects the space diagonal.
[4.1.3.2] By symmetry it suffices to consider 0≤d≤3a/2.
For 0≤d≤a/3 the intersection
forms an equilateral triangle.
[4.2.0.1] In this case d is related to the voxel porosity ψ
by
and the area of the triangle is
[4.2.0.2] For the range a/3≤d≤3a/2
the intersection forms a hexagon.
[4.2.0.3] In this case the analogous results are
| dψ,aa=32-cosarccos22ψ-1/3+π3 | | (21) |
and
| Ad,a=323d2-33d-a2. | | (22) |
[4.2.0.4] The specific surface area of a voxel with grey value
g is then
computed from
eqs. (19) and (20)
for 1≤g≤36
or from
eqs. (21) and (22)
for 37≤g≤108
with ψ=1-g/216.
[4.2.0.5] For g>108, i.e. ψ smaller than roughly 1/2,
equations (19), (20) are used for
180≤g≤215, while
(21), (22) are used for
109≤g≤179,
but now in both cases with ψ=g/216.
[4.2.0.6] The second line in Table 3 is then obtained
by inserting eq.(23)
into eq. (18) with b=mf.
[4.2.1.1] The last line in Table 3 gives the specific internal
surface Smeasureda
calculated directly using the algorithm from [30].
[4.2.1.2] The data are obtained by averaging segmented 10243-blocks.
[4.2.1.3] The segmentation threshold was chosen by maximizing the variance
of the grey scale histogram [29].
[4.2.1.4] For a=8a0,4a0,2a0 all blocks were included
into the average, for a=a0 half of the blocks, and
for a=a0/2 ten percent randomly chosen blocks were
averaged in the measurement.
[4.2.1.5] The calculation of Smeasureda
took approximately 1100 hours CPU time (without segmentation), while
the mean field estimate Smfa
can be obtained (e.g. within Matlab) directly from the
histogram Mg,a at virtually no computational cost.