Sie sind hier: ICP » R. Hilfer » Publikationen

4 Application Example

[387.2.1] The purpose of this section is to show that the previous theoretical framework can be used directly for predicting transport in porous media quantitatively and without free macroscopic fit parameters. [387.2.2] The theory presented above allows a quantitative micro-macro transition in porous media and opens the possibility to determine the elusive “representative elementary volume” needed for macroscopic theories in a quantitative and property specific manner.

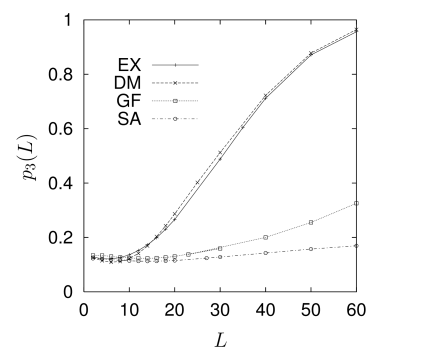
[387.3.1] In Reference [7] a fully threedimensional experimental sample of Fontainebleau sandstone was compared with three geometric models, some of which had not only the same porosity and specific internal surface area but also the same correlation function G⁢r. [387.3.2] A large number of the geometric quantities discussed above was calculated in [7]. [387.3.3] For a discussion on the influence contact of distrtributions see [29]. The total fraction of percolating cells, defined in equation (47) above, was measured in [7] for Fontainebleau and some of its models. Figure 1 shows the total fraction of percolating cells as a function of length scale (side length of measurement cells).

Figure 1: Total fraction of percolating cells for Fontainebleau sandstone (EX) and three of its models (DM,GF,SA) as discussed in Reference [7].

[page 388, §1]    [388.1.1] It turns out that the quantity p3⁢L displayed in Figure 1 correlates very well with transport properties such as the hydraulic permeability. [388.1.2] Recently transport properties such as the permesbilities and formation factors of the Fontainebleau sandstone and its geometries were calculated numerically exactly by solving the appropriate microscopic equations of motion on the computer [28]. [388.1.3] Some of the results are summarized in Table 1 below.

Table 1: Physical transport properties of Fontainebleau sandstone and three geometric models for it (see [7]). σi⁢i is the conductivity in the direction i=x,y,z in units of 10-3⁢σP, where σP is the conductivity of thematerial filling the pore space. ki⁢i is the permeability in the direction i=x,y,z in mD.
EX DM SA GF
kz⁢z[mD] 692 923 35 34
ky⁢y[mD] 911 581 22 35
kx⁢x[mD] 790 623 20 36
σz⁢z[10-3⁢σP] 18.5 26.2 1.35 2.05
σy⁢y[10-3⁢σP] 21.9 17.0 0.87 1.97
σx⁢x[10-3⁢σP] 20.5 17.1 0.96 1.98

[388.2.1] One sees from Table 1 that while EX  and DM  are very similar in their permeabilities and formation factors the samples EX  and GF  have significantly lower values with GF  being somewhat higher than SA. The same relationship is observed in Figure 1 for the percolation properties. [388.2.2] These results show that the purely [page 389, §0]    geometrical local percolation probabilities correlate surprisingly well with hydraulic permeability and electrical conductivity that determine physical transport.