II Scaling limits

[65.1.2.1] Consider a macroscopic classical continuous system within a cubic subset of Rd with volume V and linear extension L. [65.1.2.2] The finite macroscopic volume V=Ld is partitioned into N mesoscopic cubic blocks of linear size ξ. [65.1.2.3] The coordinate of the center of each block is denoted by y→j(j=1,…,N). [65.1.2.4] Each block is further partitioned into M microscopic cells of linear size a whose coordinates with respect to the center of the block are denoted as x→i(i=1,…,M). [65.1.2.5] The position vector for cell i in block j is y→j+x→i. [65.1.2.6] This partitioning of Rd is depicted in Figure 1 for d=2 and M=N=25. [65.1.2.7] The number of blocks is given by

while the number of cells within each block is

[65.2.0.1] The total number of cells inside the volume V is then N⁢M=L/ad.

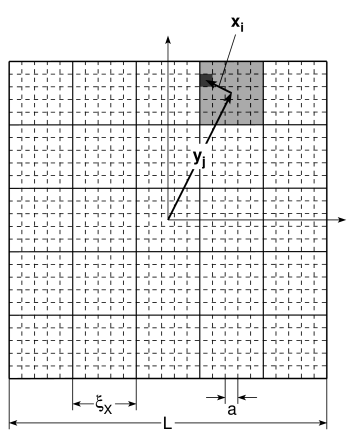
[65.2.0.2] Let the physical system enclosed in V be descriable as a classical field theory with timeindependent fields φ→(z→,t=0)=φ→(z→) and a local microscopic configurational Hamiltonian density

where ∂μ=∂/∂xμ(μ=1,…,d) denotes partial derivatives. [65.2.0.3] A particular example for the potential U⁢φ→ would be the ϕ4-model for which

where the parameters m and g are the mass and the coupling constant. [65.2.0.4] For future convenience the parameters of the field theory are collected into the parameter vector Π→=Π1,Π2,…=J,m,g,…. [65.2.0.5] The partitioning introduced above allows two regularizations into a lattice field theory. [65.2.0.6] On the mesoscopic level the regularized block action representing the total configurational energy of a single block (e.g. for block j) reads

where x→i,x→kj denotes nearest neighbour pairs of cells inside block j,(j=1,…,N) such that each pair is counted once. [65.2.0.7] On the macroscopic level one has the discretized action between blocks (representing the total configurational energy)

where now y→j,y→k denotes nearest neighbour blocks. [65.2.0.8] Although the overall form of the discretizations is identical for HM⁢N and HM⁢N the macroscopic discretized fields ϕ→ and interactions J,U may in general require renormalization in the infinite volume and continuum limit, and are therefore denoted by different symbols. [65.2.0.9] Rearranging eq. (2.5) the macroscopic discretized action HM⁢N⁢ϕ→ is related to the mesoscopic discretized action HM⁢N⁢φ→⁢y→j through

expressing a decomposition into bulk plus surface energies. [65.2.0.10] Here ∑~ expresses a summation over nearest neighbour [page 66, §0]    cells in the surface layers of adjacent blocks such that each pair of adjacent block surface cells is counted once. [66.1.0.1] Conventional field theory or equilibrium statistical mechanics assumes that the surface term which is of order O⁢N⁢Md-1/d becomes negligible compared to the bulk term which is of order O⁢N⁢M in the field-theoretic continuum limit.

[66.1.1.1] Consider now a scalar local observableXM⁢N⁢φ→⁢x→i+y→j (composite operator) fluctuating from cell to cell. [66.1.1.2] The fluctuations generally define a correlation length ξX⁢Π→ whose magnitude depends on the observable in question and the parameters Π→ in the Hamiltonian. [66.1.1.3] The reconstruction of the continuum theory from its discretization is usually carried out in two steps [24]. [66.1.1.4] First one takes the (thermodynamic) infinite volume limit L→∞ at constant a as the limit of canonical (Boltzmann-Gibbs) probability measures in the finite volume. [66.1.1.5] The existence of this limit requires stability and temperedness of the interaction potentials [25]. The limit amounts to setting N=1 and thus HM⁢1=HM⁢1.

[66.1.2.1] Given the existence of the infinite volume limit one studies the scaling limit a→0,Π→→Π→c of the regularized infinite-volume theory. [66.1.2.2] This field theoretic limit in general requires the renormalization of the action HM⁢1⁢φ→. [66.1.2.3] The quantities of main interest are the correlation functions

within a single block here chosen to be the one at the origin, i.e. y→1=0→. [66.1.2.4] The normalization constant Z is the partition function, the measure μ⁢φ→;a,L,Π→ is the finite volume lattice probability distribution on the space of field configurations, and the notation …Π→ for the expectation value expresses its dependence on the parameters in the Hamiltonian. [66.1.2.5] The correlation functions (2.9) are plagued the well known short distance singularities in the continuum limit a→0. [66.1.2.6] The standard approach [24] to this problem is to keep a>0 fixed and to use instead a lattice rescaling procedure in which the auxiliary rescaling factor b∝a-1→∞ diverges. [66.1.2.7] This keeps the theory explicitly finite at all steps. [66.1.2.8] Thus the field theoretic continuum theory is defined through the limiting renormalized correlation functions

where A⁢b is the field renormalization. [66.1.2.9] The parameters Π→ approach a critical point Π→c=Π→⁢∞ such that the rescaled correlation length

remains nonzero. [66.2.0.1] The field theoretical continuum or scaling limit is called “massive” or “massless” depending on whether the rescaled correlation length approaches a finite constant or diverges to infinity. [66.2.0.2] Because a>0 is fixed equations (2.2) and (2.11) imply b∝ξ∝M1/d in the massive scaling limit, and this allows to rewrite equation (2.10) as

if the limit exists. [66.2.0.3] In that case the renormalization factor D⁢M has the form

by virtue of the relation

which follows generally from renormalization group theory [26]. [66.2.0.4] Here dX is the anomalous dimension of the operator X.

[66.2.1.1] The ensemble limit introduced in [20] is a way of defining infinite volume continuum averages from the discretized theory in a finite volume without actually calculating the measure μ⁢φ→,0,∞,Π→c explicitly. [66.2.1.2] The idea is to focus on the one point functions given by (2.12) with n=1 as

where independence of x→i by virtue of translation invariance has been used in the first and the last equality. [66.2.1.3] At criticality these functions contain information about fluctuations through the renormalization factor D⁢M for field averages.

[66.2.2.1] For a given field configuration the fluctuating local observable inside cell i(i=1,…,M) of block j(j=1,…,n) will again be denoted by XM⁢N⁢φ→⁢y→j+x→i as defined above and illustrated in Figure 1. [66.2.2.2] The block variables

j=1,…,N are defined by summing the cell variables and the ensemble variable [page 67, §0]

is obtained by summing the block variables. For a>0 the ensemble limit is defined as the limit

where C0 is a constant. [67.1.0.1] In the ensemble limit L∼ξX⁢Π→2 as compared to L∼ξX⁢Π→ in the fieldtheoretic scaling limit. [67.1.0.2] The difference to the field theoretic scaling limit is that thermodynamic (L→∞), continuum (a→0) and critical (Π→→Π→c) limit are taken simultaneously. [67.1.0.3] In this way an infinite ensemble of regularized infinite classical continuum systems is generated. [67.1.0.4] The elements of the ensemble are replicas of one and the same system governed by the Hamiltonian density H⁢φ→. [67.1.0.5] Thus the ensemble limit generates an ensemble in the sense of statistical mechanics.

[67.1.1.1] The critical or noncritical averages X∞⁢1Π→ can be calculated in the ensemble limit as

[67.1.1.2] This equation states that macroscopic ensemble averages can either be calculated using equations (2.9) in the traditional scaling limit or directly using equations (2.18) and (2.19) in the ensemble limit. [67.1.1.3] Equation (2.21) gives the connection between the scaling limit and the ensemble limit. [67.1.1.4] Note that the validity of eq. (2.21) requires the existence of the renormalized field theory. [67.1.1.5] Thus the left hand side of (2.21) cannot be calculated at anequilibrium phase transitions [21, 22] while the right hand side can still be calculated in such cases.

[67.1.2.1] The main difference of the ensemble limit as compared to other scaling limits is that the three limits a→0,L→∞,Π→→Π→c are simultaneously performed while in other limits only two of these limits are taken simultaneously. [67.1.2.2] There are 23=8 ways of performing the scaling limit with the three variables a,L,Π→ depending on whether a particular variable is set equal to its limiting value or not. [67.2.0.1] The different possibilities are summarized in Table I. [67.2.0.2] Note that only the ensemble limit (1.) and the related critical limit (7.) in an infinite continuum theory yield an infinite number of uncorrelated blocks. [67.2.0.3] The close relation between the ensemble limit and the massive finite size scaling limit (5.) is apparent if N0≫1.