VI Scaling functions
[72.1.4.1] This section discusses how the general theory above may be used to
obtain finite size scaling functions at the critical point.
[72.2.1.1] The finite size scaling function p~Xx,y for the
probability density px,ξ,L of the observable X is defined
through an equation analogous to (1.3) by
| px,L,ξ=LddX-d*/d-d*p~XxLddX-d*/d-d*,L/ξd* | | (6.1) |
where dX is the anomalous dimension of X.
[72.2.1.2] The ensemble limit yields explicit analytical expressions
for the scaling functions p~Xx,y at the
critical point.
[72.2.1.3] This is seen from (4.11) as well as from
(4.4) which become identical in the ensemble limit
if ϖX<2.
[72.2.1.4] If X is identified as the macroscopic (thermodynamic)
equivalent of the microscopic observable Y then it follows from
(4.4) and (4.11) that the finite ensemble scaling
functions are given as
| p~XESx,y=p~YESx,y=hx;ϖX,ζX,0,D | | (6.2) |
if 1<ϖX<2.
[72.2.1.5] The superscript is a reminder for
the ensemble limit.
[72.2.1.6] The point ϖX=1 corresponding
to first order transitions is singular and will not be
discussed here.
[72.2.1.7] For
ϖX=2 on the other hand the
thermodynamic form (4.4) yields a simple Gaussian
while the fieldtheoretic form (4.11) gives
| p~XESx,y=14πDy2dX-dexp-x24Dy2dX-d. | | (6.3) |
[72.2.1.8] This is the scaling function conjectured in [7] for the order
parameter density on the basis of a Gaussian approximation.
[72.2.1.9] Note
that this scaling function, contrary to those for ϖX<2,
does depend on the variable y separately.
[72.2.1.10] Note also that the
order parameter generally has anomalous dimension dΨ<d/2
and thus this scaling form for the order parameter distribution
is expected to arise in the vicinity but not directly at the
critical point.
[72.2.2.1] Another source for the dependence of the scaling function
p~Ψx,y for the order parameter
distribution on y is the appearance of the nonuniversal
cutoff function R in the finite size scaling limit of equation
(3.18).
[72.2.2.2] With equation (3.18) and introducing
the abbreviations Rx,L/ξ=Rx,∞,L/ξd,∞,
hx=hx;ϖX,ζX,0,D and Hx=Hx;ϖX,ζX,0,D
the analogue of equation (6.2) reads
| p~XFSSx,y=Rx,yhx+Hx∂Rx,y∂x : for x≤0Rx,yhx-1-Hx∂Rx,y∂x : for x>0 | | (6.4) |
for the finite size scaling limit.
[72.2.2.3] Thus it is seen that the finite ensemble
scaling function h corresponds to the universal part of the finite size
scaling function which is independent of y while the cutoff function R
is responsible
[page 73, §0]
for the dependence on y and adds a nonuniversal part.
[73.1.1.1] The analytical expressions (3.5) and (3.12) for
the universal part of critical finite size scaling functions
can be employed to evaluate the scaling functions numerically.
[73.1.1.2] In this effort the symmetry relation [28]
| h-x,ϖX,ζX,0,1=hx;ϖX,-ζX,0,1 | | (6.5) |
reduces the computational effort.
[73.1.1.3] Moreover equation (6.5)
suggests a relation with the phenomenon of spontaneous symmetry
breaking within the present approach.
[73.1.1.4] In this view the two scaling
functions hx;ϖX,±ζX,0,1 represent the two pure
phases, and thus on general thermodynamic grounds the full scaling
function is expected to become a convex combination
| p~Xx=p~XESx,y=shx;ϖX,ζX,0,D+1-shx;ϖX,-ζX,0,D | | (6.6) |
of two extremal phases.
[73.1.1.5] The relation may be generalized
to several phases or asymmetric situations.
[73.1.2.1] Consider now an ordinary critical point with a global symmetry
such as in the Ising models.
[73.1.2.2] Let X=Ψ be the order parameter
which is assumed to be normalized such that D=1.
[73.1.2.3] Then ϖX
becomes ϖΨ=1+1/δ where δ is the
equation of state exponent.
[73.1.2.4] Abbreviating ζΨ as ζ
the scaling function in equation (6.6) becomes
| p~Ψx;δ,ζ,s=shx;1+1/δ,ζ,0,1+1-shx;1+1/δ,-ζ,0,1. | | (6.7) |
[73.1.2.5] For the symmetric case s=1/2 the function
p~Ψx;δ,ζ,s
is displayed in Figures 2, 3 and 4 for δ=3,5,15 and several
choices of ζ.
[73.1.2.6] The symmetrization s=1/2 in (6.7)
corresponds to an “equal weight rule” which is known to apply for
first order transitions [42].
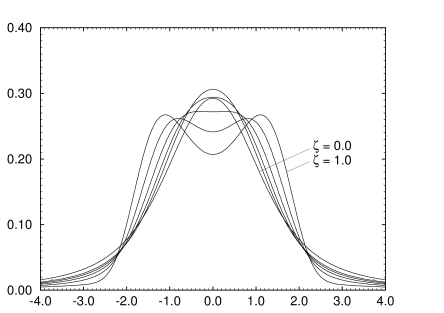
[73.1.2.7] Figure 2 shows the case δ=3 which is the value for
the universality class of mean field models.
[73.1.2.8] The six values
for ζ in Figure 2 through 4 are ζ=0.0,0.6,0.7,0.8,0.9,1.0.
[73.1.2.9] The case ζ=1.0 corresponds to the double peak structure
with the widest peak separation while the value ζ=0.0
corresponds to the singly peaked function whose maximum has the
smallest height.
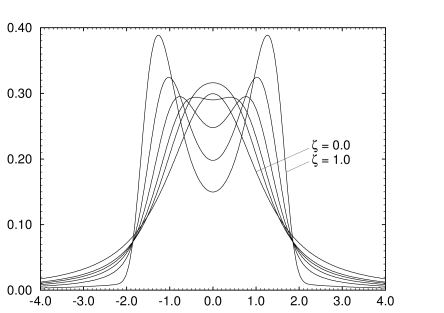
[73.1.2.10] Figure 3 shows the case δ=5 which
is close to the value of δ≈4.8 [16] for the
threedimensional Ising model.
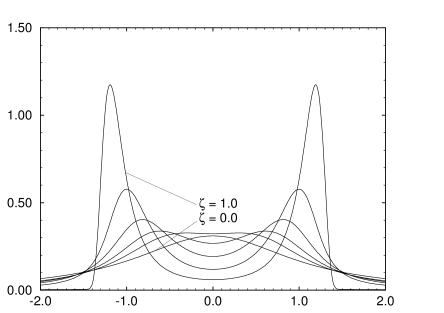
[73.1.2.11] The value δ=15 in Figure 4
is the value for the two dimensional Ising universality class.
[73.1.2.12] The scaling functions displayed in Figures 2 through 4 are
consistent with published data on critical scaling
functions [7, 43, 44].
[73.1.2.13] Moreover it is
seen that the universal shape parameter
ζ is related
to the type of boundary conditions.
[73.1.2.14] Free boundary conditions
apparently correspond to smaller values of the
universal shape parameter ζ than periodic
boundary conditions.
[73.1.2.15] This correspondence between the
value of ζ and the applied boundary conditions
is not expected to be one to one.
[73.1.2.16] The value of ζ
may be influenced by other universal factors such
as the type or symmetry of the pure phases.
[page 74, §0]
[74.1.0.1] On the other
hand the boundary conditions may also influence other
parameters such as the value of the symmetrization s.
[74.1.0.2] This is expected for boundary conditions which do
not preserve the symmetry.
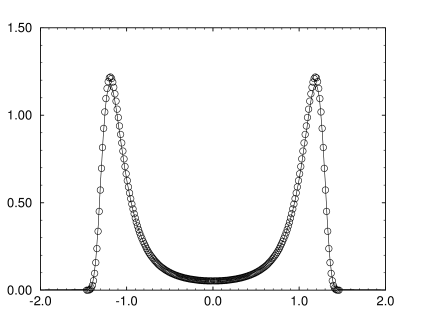
[74.1.1.1] Figure 5 shows that the scaling functions are not merely
consistent but also in good
quantitative agreement with Monte-Carlo simulations
of the twodimensional Ising model [43, 44, 45]
where the exact value of δ and the location of the
critical point for the infinite system are known.
[74.1.1.2] The open
circles in Figure 5 represent the smooth interpolation
through the data published in [43, 44, 45].
[74.1.1.3] The solid line is the analytical prediction shown in Figure 4
for ζ=1.
[74.1.1.4] For the comparison the nonuniversal scaling
factors which were chosen to yield unit norm and variance
in [43, 44, 45] were matched to those of the
theoretical curve.
[74.1.1.5] The excellent agreement between theory and simulation suggests
to identify the value ζ=1 with periodic boundary
conditions.
[74.1.1.6] It is however not clear whether this identification
will hold more generally.