Sie sind hier: ICP » R. Hilfer » Publikationen

5 Results

[190.1.1] The results for ω=0 will be expressed via the so called correlation factor f. [190.1.2] It is a measure which is often used to characterize the amount by which the self diffusion coefficient of a tracer particle in a lattice gas differs from its mean field value given by the vacancy concentration. [190.1.3] All results will be presented and discussed with the conventions ω=1, p′′⁢0=1, and assuming a unit lattice constant. [190.1.4] In these dimensionless units f is defined by the equation D⁢0=f⁢1-p or, more generally,

f=D⁢0D⁢∞(5.1)

because for our hopping models 1-p=D⁢∞. [190.1.5] In the limit p→1 exact results for the correlation factor are known for the case τ=1 (and b=1)[11, 13, 14]. [page 191, §0]    [191.0.1] For the hexagonal lattice one has f=1/3, while f=0.781.. for the fcc lattice. [191.0.2] These values will be used below to determine c in eq. (4.2).

[191.1.1] We now have to solve eq. (3.10) in conjunction with eqs. (3.13) and (4.4) for the cases of interest, the hexagonal and face centered cubic lattice. [191.1.2] The lattice Greens functions for these situations are well known and can be expressed in terms of the complete elliptic integral of the first kind

K⁢m=∫0π/21-m⁢sin2⁡ϕ-1/2⁢d⁢ϕ.(5.2)

[191.1.3] For the hexagonal lattice we have

G⁢x=-2⁢3+xπ⁢2+x3/2⁢6+x1/2⁢K⁢16⁢x+3x+23⁢x+6.(5.3)

For the fcc lattice the Greens function is given by

G⁢x=-1π2⁢4+x-1⁢K⁢x+⁢K⁢x-(5.4)

where

x±2=4+x4-2⁢116⁢4+x41/2-x41/24+4+x41/2±3+x41/2.(5.5)

[191.1.4] We now solve eq. (3.10) iteratively on the computer. [191.1.5] We stop the iteration when the maximal relative error between two consecutive solutions falls below 108. [191.1.6] The resulting A0⁢u is then used to calculate D⁢u according to eqs. (3.13) and (4.4). [191.1.7] The results are displayed in Figures 2 through 10.

[191.2.1] First we determine the proportionality constant c in eq. (4.2). [191.2.2] This is achieved by requiring that the calculated correlation factor reproduces the known exact results for the limit p=1,τ=1,b=1. [191.2.3] We find chcx≈1.00for the hexagonal lattice, and cfcc≈0.16for the fcc lattice. [191.2.4] These numbers are difficult to determine numerically, and we estimate the error to be roughly 0.03. [191.2.5] In all subsequent calculations we then use these values for c.

Figure 2: Correlation factor f as function of blocker concentration p for the face centered cubic lattice (b=1, c=0.16). The crosses are the simulation results of Ref. [7] for the case τ=1. The circles are simulation results from Ref. [10] for the case τ=∞. The dashed line is obtained by using the exact value pc=0.198...from Ref. [8] instead of the effective medium value pc=1/6.
Figure 3: Correlation factor f vs. blocker concentration p and ratio of hopping rates τ for the hexagonal lattice (b=1, c=1). The crosses are simulation results from Ref. [12] for the case τ=1.

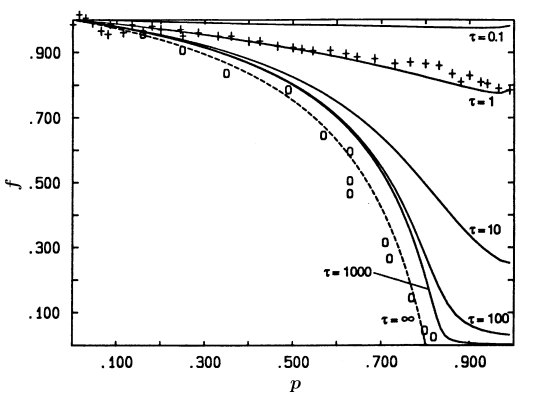
[page 193, §1]    [193.1.1] In Figure 2 we have extracted the correlation factor from D⁢0 and plotted it versus blocker concentration p. [193.1.2] All curves are for the uncorrelated case, i. e.  b=1, on the fcc lattice. [193.1.3] We give results for τ=0.1,1,10,100,1000and τ=∞. [193.1.4] The crosses are the results of the Monte Carlo simulation for the case τ=1 taken from Ref. [7]. [193.1.5] The circles are MC-results for τ=∞ and were taken from Ref. [10]. [193.1.6] Clearly there will be a discrepancy for this case because our results are approximate and for bond percolation while the simulation is exact and for site percolation. [193.1.7] An immediate problem is the value of pc for which the effective medium theory gives pc=1/6 while the exact value is pc=0.198.. [8]. [193.1.8] If we simply use the exact value for pc in our calculation we obtain the dashed line displayed in Fig. 2 which is found to be in good agreement. 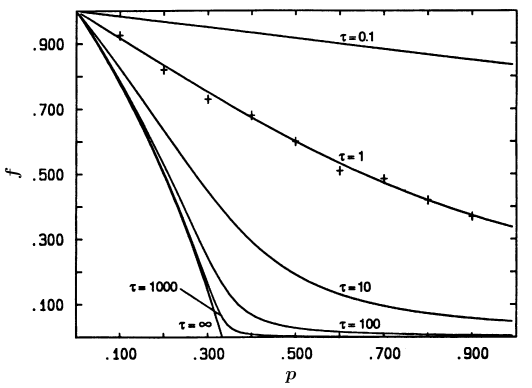[193.1.9] In Fig. 3 we plot f vs. p for the hexagonal lattice. [193.1.10] Here the simulations have been taken from Ref. 10. [193.1.11] Keeping in mind that there are no free parameters (remember b=1) we find very good agreement for both lattices. [193.1.12] However, additional simulation data especially for τ in the range 1<τ<∞, and a more accurate determination of c are required to fully evaluate the quality of the theoretical results. [page 194, §0]    [194.0.1] We now turn to the results for our primary objective, the frequency dependent diffusion coefficient.

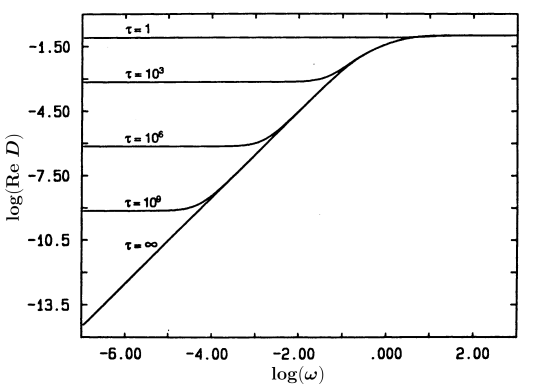
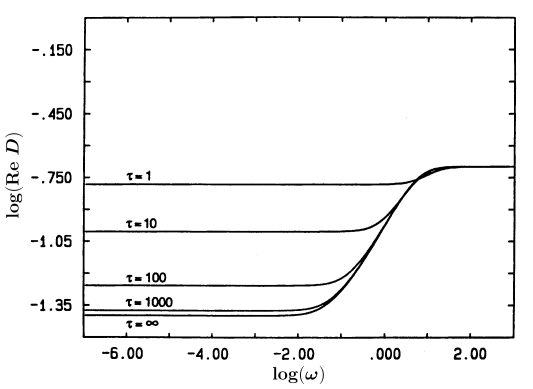
[194.1.1] We consider first the uncorrelated case b=1 on the fcc-lattice. [194.1.2] In Figure 4 and Figure 5 we plot Re⁡D⁢ω over ten decades in frequency on a log-log plot. [194.1.3] Figure 4 corresponds to a blocker concentration p=0.9 which is below the percolation threshold for vacancies, and shows the results for τ=1,103,106,109and ∞. [194.1.4] Figure 5 has p=0.8 and τ=1,10,100,1000. [194.1.5] From Figure 4 we see immediately that below the percolation threshold D⁢ω vanishes quadratically with frequency for τ=∞. [194.1.6] This behaviour is well known from the analysis of the EM theory for the frozen case. [194.1.7] For τ<∞ we find a crossover to a constant proportional to 1/τ. [194.1.8] This could have been expected because the blocker motion now allows the A—particle to get through the network although the vacancy concentration at each instant is below pc. [194.1.9] The mobility of the A-particles will be completely determined by the mobility of the blockers. [page 197, §0]    [197.0.1] The crossover frequency is seen to vary as ωτ∼τ-1/2. [197.0.2] This will be discussed further in the next section. [197.0.3] On the other hand above the vacancy threshold Figure 5 shows that the effect of the blocker rearrangement is only noticeable for τ values smaller than roughly 104. [197.0.4] Indeed one expects that the effect of blocker motion will become negligible if 1/τ is much smaler than the d. c. conductivity in the frozen case which is proportional to 1-p-pc.

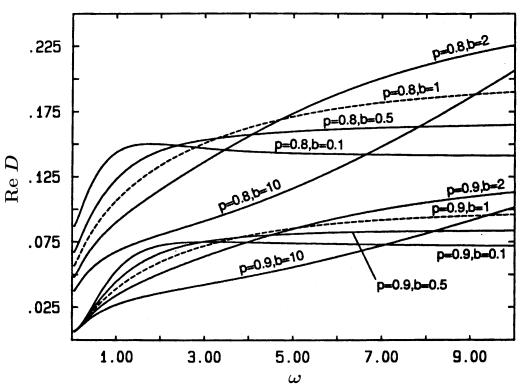
Figure 4: Real part of the genaralized diffusion coefficient Re⁡D⁢ω for the fcc-lattice as a function of frequency ω in a logarithmic plot for several values of τ and p=0.9, b=1 (C=0.16).
Figure 5: Real part of the genaralized diffusion coefficient Re⁡D⁢ω for the fcc-lattice as a function of frequency ω in a logarithmic plot for several values of τ and p=0.8, b=1 c=0.16.

[197.1.1] In Figures 6 and 7 we now turn to the correlated case, i. e.  b≠1. [197.1.2] Again we consider the fcc-lattice and plot the real (Fig. 6) and imaginary (Fig. 7) part of D⁢ω for the two concentrations p=0.8 and p=0.9 with fixed τ=100 but variable b. [197.1.3] We have chosen b=0.1, 0.5, 1, 2, 10 for the correlation factor. [197.1.4] The case b=1 is included as a reference and has been distinguished graphically by a dashed line. [197.1.5] As before the real part approaches a constant as ω→0 irrespective of p because τ is finite. [197.1.6] A new phenomenon however is the appearance of nonmonotonous behaviour for b=0.1. [197.1.7] In this case Re⁡D⁢ω is found to increase at low frequencies, and to decrease at high frequencies thereby exhibiting a maximum at a finite frequency. [197.1.8] In general Re⁡D⁢ω is found to decrease as b→0 at high frequencies, and to increase at low frequencies. [197.1.9] The reverse is seen for b→∞. [197.1.10] This will also be discussed in the next section in more detail. [197.1.11] For the imaginary part of D⁢ω we find a change of sign for sufficiently small b<1. [197.1.12] See for example the case p=0.8, b=0.1. [197.1.13] On the other hand for p=0.9, b=0.1 there is no change of sign in the imaginary part while the real part still shows a maximum.

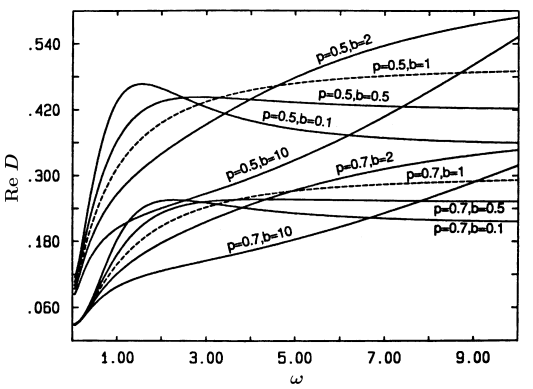
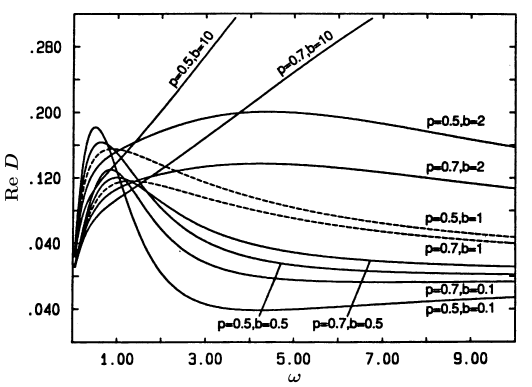
[197.2.1] The same calculations have been performed for the hexagonal lattice. [197.2.2] The results are displayed in Figures 8 and 9. [197.2.3] The only difference lies in the parameter values. [197.2.4] We have chosen different concentrations, p=0.5, 0.7, b=0.1 and fixed τ at τ=10. [197.2.5] The results show qualitatively the same behaviour as for the fcc-lattice.

Figure 6: Real part of D⁢ω for the fcc-lattice as a function of frequency in a linear plot for fixed τ=100, and values for b and p as indicated. The dashed line corresponds to the uncorrelated case b=1.
Figure 7: Imaginary part of D⁢ω for the fcc-lattice as a function of frequency in a linear plot for fixed τ=100, and values for b and p as indicated. The dashed line is for the uncorrelated case b=1.
Figure 8: Real part of D⁢ω for the hexagonal lattice as a function of frequency in a linear plot for fixed τ=10, and values for b and p as indicated. The dashed line indicates the uncorrelated case b=1.
Figure 9: Imaginary part of D⁢ω for the hexagonal lattice as a function of frequency in a linear plot for fixed τ=10, and values for b and p as indicated. The dashed line corresponds to the uncorrelated case b=1.

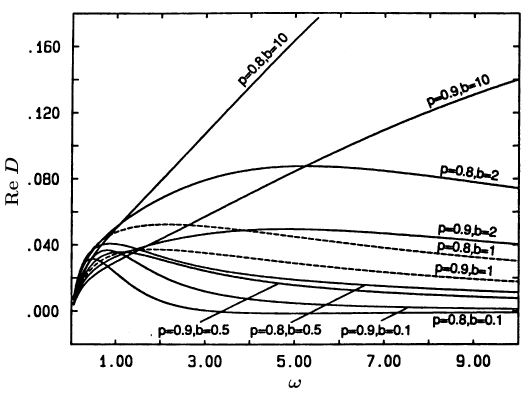
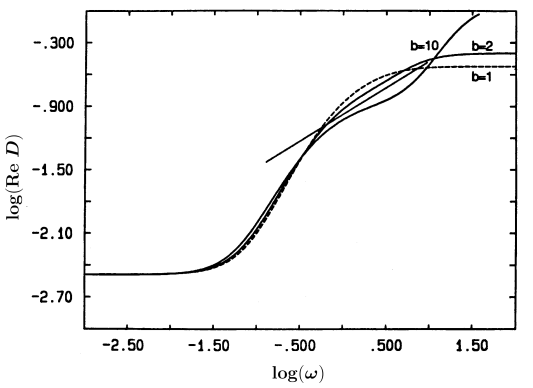
[197.3.1] In Figure 10 we have plotted some results for the correlated case (b≠1) in a log-log plot. [197.3.2] We show Re⁡D⁢ω for p=0.7, τ=100 and b=1,2,10 on the hexagonal lattice. [197.3.3] We note that as a consequence of the correlations the crossover into the constant high frequency limit is smeared out and resembles a power law over more than a decade in frequency. [197.3.4] This is particularly apparent for the case b=2.

Figure 10: Real part of D⁢ω for the hexagonal lattice plotted logarithmically against frequency for p=0.7, τ=100 and b=1,2,10. The slope of the straight line is roughly 0.5.

[page 198, §0]    [198.1.1] For reference we have included a straight line into the graph whose slope is found to be roughly 0.5. [198.1.2] We remark that such a power law behaviour for the frequency dependent conductivity is often found experimentally in disordered systems. [198.1.3] As a particular example we mention Na-β-alumina where the ionic transport is also known to be highly correlated[34].