| 1 |
G.W. Scott-Blair and J.E. Caffyn.
An application of the theory of quasi-properties to the treatment of
anomalous stress-strain relations.
Phil. Mag., 40:80, 1949.
|
| 2 |
H. Berens and U. Westphal.
A Cauchy problem for a generalized wave equation.
Acta Sci. Math. (Szeged), 29:93, 1968.
|
| 3 |
K.B. Oldham and J.S. Spanier.
The replacement of Fick’s law by a formulation involving
semidifferentiation.
J. Electroanal. Chem. Interfacial Electrochem., 26:331, 1970.
|
| 4 |
M. Caputo and F. Mainardi.
Linear models of dissipation in anelastic solids.
Riv.Nuovo Cim., 1:161, 1971.
|
| 5 |
K.B. Oldham and J.S. Spanier.
The Fractional Calculus.
Academic Press, New York, 1974.
|
| 6 |
R. Hilfer.
Classification theory for anequilibrium phase transitions.
Phys. Rev. E, 48:2466, 1993.
|
| 7 |
R. Hilfer.
On a new class of phase transitions.
In W.P. Beyermann, N.L. Huang-Liu, and D.E. MacLaughlin, editors,
Random Magnetism and High-Temperature Superconductivity, page 85,
Singapore,, 1994. World Scientific Publ. Co.
|
| 8 |
R. Hilfer.
Exact solutions for a class of fractal time random walks.
Fractals, 3(1):211, 1995.
|
| 9 |
R. Hilfer.
Fractional dynamics, irreversibility and ergodicity breaking.
Chaos, Solitons & Fractals, 5:1475, 1995.
|
| 10 |
R. Hilfer.
Foundations of fractional dynamics.
Fractals, 3:549, 1995.
|
| 11 |
R. Hilfer.
An extension of the dynamical foundation for the statistical
equilibrium concept.
Physica A, 221:89, 1995.
|
| 12 |
R.L. Bagley and P.J. Torvik.
A theoretical basis for the application of fractional calculus to
viscoelasticity.
J. Rheology, 27:201, 1983.
|
| 13 |
R.L. Bagley and P.J. Torvik.
On the fractional calculus model of viscoelastic behaviour.
J. Rheology, 30:133, 1986.
|
| 14 |
W. Wyss.
The fractional diffusion equation.
J. Math. Phys., 27:2782, 1986.
|
| 15 |
W.R. Schneider and W. Wyss.
Fractional diffusion and wave equations.
J. Math. Phys., 30:134, 1989.
|
| 16 |
A.M.A. El-Sayed.
Fractional-order diffusion-wave equation.
Int. J. Theor. Phys., 35:311, 1996.
|
| 17 |
A. Compte.
Stochastic foundations of fractional dynamics.
Phys.Rev. E, 55:4191, 1996.
|
| 18 |
T.F. Nonnenmacher and W.G. Glöckle.
A fractional model for mechanical stress relaxation.
Phil. Mag. Lett., 64:89, 1991.
|
| 19 |
L. Gaul, P. Klein, and S. Kempfle.
Damping description involving fractional operators.
Mechanical Systems and Signal Processing, 5:81, 1991.
|
| 20 |
H. Beyer and S. Kempfle.
Definition of physically consistent damping laws with fractional
derivatives.
A. angew. Math. Mech., 75:623, 1995.
|
| 21 |
R.R. Nigmatullin.
The realization of the generalized transfer equation in a medium with
fractal geometry.
phys. stat. sol. b, 133:425, 1986.
|
| 22 |
S. Westlund.
Dead matter has memory !
Physica Scripta, 43:174, 1991.
|
| 23 | G. Jumarie.
A Fokker-Planck equation of fractional order with respect to
time.
J. Math. Phys., 33:3536, 1992.
|
| 24 |
H. Schiessel and A. Blumen.
Fractal aspects in polymer science.
Fractals, 3:483, 1995.
|
| 25 |
G. Zaslavsky.
Fractional kinetic equation for Hamiltonian chaos.
Physica D, 76:110, 1994.
|
| 26 |
G. Zaslavsky.
From Hamiltonian chaos to Maxwell’s demon.
Chaos, 5:653, 1995.
|
| 27 |
E. Stein and G. Weiss.
Introduction to Fourier Analysis on Euclidean Spaces.
Princeton University Press, Princeton, 1971.
|
| 28 |
C. Berg and G. Forst.
Potential Theory on Locally Compact Abelian Groups.
Springer, Berlin, 1975.
|
| 29 |
A.P. Prudnikov, Yu.A. Brychkov, and O.I. Marichev.
Integrals and Series, volume 4.
Gordon and Breach, New York, 1992.
|
| 30 |
B.V. Gnedenko and A.N. Kolmogorov.
Limit Distributions for Sums of Independent Random Variables.
Addison-Wesley, Cambridge, 1954.
|
| 31 |
W. Feller.
An Introduction to Probability Theory and Its Applications,
volume II.
Wiley, New York, 1971.
|
| 32 |
F. Oberhettinger.
Tables of Mellin Transforms.
Springer Verlag, Berlin, 1974.
|
| 33 |
I.A. Ibragimov and Yu.V. Linnik.
Independent and Stationary Sequences of Random Variables.
Wolters-Nordhoff Publishing, Groningen, 1971.
|
| 34 |
S. Bochner.
Harmonic Analysis and the Theory of Probability.
University of California Press, Berkeley, 1955.
|
| 35 |
K. Yosida.
Functional Analysis.
Springer, Berlin, 1965.
|
| 36 |
A.V. Balakrishnan.
Fractional powers of closed operators and the semigroups generated by
them.
Pacific J. Math., 10:419, 1960.
|
| 37 |
U. Westphal.
Ein Kalkül für gebrochene Potenzen infinitesimaler
Erzeuger von Halbgruppen und Gruppen von Operatoren.
Compositio Math., 22:67, 1970.
|
| 38 |
L. Bieberbach.
Lehrbuch der Funktionentheorie, volume II.
Teubner, Leipzig, 1931.
|
| 39 |
W.R. Schneider.
Completely monotone generalized Mittag-Leffler functions.
Expo. Math., 14:3, 1996.
|
| 40 |
P.L. Butzer and R. J. Nessel.
Fourier Analysis and Approximation, volume 1.
Birkhäuser Verlag, Basel, 1971.
|
| 41 |
R. Hilfer and L. Anton.
Fractional master equations and fractal time random walks.
Phys.Rev.E, Rapid Commun., 51:848, 1995.
|
| 42 |
R. Hilfer.
On fractional diffusion and its relation with continuous time random
walks.
In A. Pekalski R. Kutner and K. Sznajd-Weron, editors, Anomalous
Diffusion: From Basis to Applications, page 77. Springer, 1999.
|
| 43 |
E.W. Montroll and G.H. Weiss.
Random walks on lattices II.
J. Math. Phys., 6:167, 1965.
|
| 44 |
M.N. Barber and B.W. Ninham.
Random and Restricted Walks.
Gordon and Breach Science Publ., New York, 1970.
|
| 45 |
J.W. Haus and K. Kehr.
Diffusion in regular and disordered lattices.
Phys.Rep., 150:263, 1987.
|
| 46 |
J. Klafter, A. Blumen, and M.F. Shlesinger.
Stochastic pathway to anomalous diffusion.
Phys. Rev. A, 35:3081, 1987.
|
| 47 |
B.D. Hughes.
Random Walks and Random Environments, volume 1.
Clarendon Press, Oxford, 1995.
|
| 48 |
B.D. Hughes.
Random Walks and Random Environments, volume 2.
Clarendon Press, Oxford, 1996.
|
| 49 |
J.K.E. Tunaley.
Some properties of the asymptotic solutions of the Montroll-Weiss
equation.
J. Stat. Phys., 12:1, 1975.
|
| 50 |
E.W. Montroll and B.J. West.
On an enriched collection of stochastic processes.
In E.W. Montroll and J.L Lebowitz, editors, Fluctuation
Phenomena, page 61, Amsterdam, 1979. North Holland Publ. Co.
|
| 51 |
G.H. Weiss and R.J. Rubin.
Random walks: Theory and selected applications.
Adv. Chem. Phys., 52:363, 1983.
|
| 52 |
A. Erdelyi (et al.).
Higher Transcendental Functions, volume III.
Mc Graw Hill Book Co., New York, 1955.
|
| 53 |
M.F. Shlesinger.
Asymptotic solutions of continuous time random walks.
J. Stat. Phys., 10:421, 1974.
|
| 54 |
M.F. Shlesinger, J. Klafter, and Y.M. Wong.
Random walks with infinite spatial and temporal moments.
J. Stat. Phys., 27:499, 1982.
|
| 55 |
C. Fox.
The 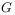 and and 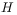 functions as symmetrical Fourier kernels.
Trans. Am. Math. Soc., 98:395, 1961. functions as symmetrical Fourier kernels.
Trans. Am. Math. Soc., 98:395, 1961.
|
| 56 |
B.L.J. Braaksma.
Asymptotic expansions and anlytic continuations for a class of
Barnes-integrals.
Compos.Math., 15:239, 1964.
|
| 57 |
A.M. Mathai and R.K. Saxena.
The 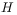 -function with Applications in Statistics and Other
Disciplines.
Wiley, New Delhi, 1978. -function with Applications in Statistics and Other
Disciplines.
Wiley, New Delhi, 1978.
|
| 58 |
H.M. Srivastava, K.C. Gupta, and S.P. Goyal.
The 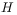 -functions of One and Two Variables with Applications.
South Asian Publishers, New Delhi, 1982. -functions of One and Two Variables with Applications.
South Asian Publishers, New Delhi, 1982.
|
| 59 |
A.P. Prudnikov, Yu.A. Brychkov, and O.I. Marichev.
Integrals and Series, volume 3.
Gordon and Breach, New York, 1990.
|
| 60 |
I.N. Sneddon.
The Use of Integral Transforms.
Mc Graw Hill, New York, 1972.
|
