Sie sind hier: ICP » R. Hilfer » Publikationen

11 Experimental Evidence

[218.2.1] If fractional time evolutions from eq. (27) with α<1 must be expected on general grounds, then they should be observable in experiment. [218.2.2] Numerous experimental examples of anomalous dynamics or strange kinetics have been identified (see [17, 18, 19, 20] and the present volume for reviews). [218.2.3] Here the example of dielectric α-relaxation in glasses is briefly discussed[53, 54], because it provides experimental data over up to 19 decades in time [55], and because the explanation of its excess wing has been a matter of debate.

Figure 1: Five different fits to the real part ε′⁢f of the complex dielectric function of propylene carbonate at T=193⁢K as a function of frequency f. Experimental data represented by crosses are from Ref. [56]. The fitting functions corresponds to an exponential (Debye), stretched exponential (KWW), Cole-Davidson [57, 58] Havriliak-Negami [59, 60] and the fractional dynamics (FD) relaxation from (40) The range over which the data were fitted is indicated by dashed vertical lines in the figure. For clarity the data were displaced vertically by half a decade each. The original location of the data corresponds to the curve labelled FD.
Figure 2: Five different fits as in Figure 1 for the imaginary part ε′′⁢f of the complex dielectric function of propylene carbonate at T=193⁢K as a function of frequency f.

[218.3.1] For every induced time evolution on G with time scale τ>0 and fractional order β⁢τ

G⁢Tβ⁢ττ⁢t=G⁢Tβ⁢ττ1⁢t⁢G⁢Tβ⁢ττ-τ1⁢t=G⁢Tβ⁢ττ1⁢t⁢G⁢Tβ⁢τ1+τ2τ2⁢t(36)

holds generally with τ=τ1+τ2. [218.3.2] A physical system typically shows different physical phenomena on different time scales τi. [218.3.3] In [53, 54] it was assumed that the second factor in eq. (36) becomes approximately fractional in the sense that

G⁢Tβ⁢τ1+τ2τ2⁢t≈G⁢Tα⁢τ2τ2⁢t(37)

holds in the weak* or strong topology with

limτ2→0⁡α⁢τ2=β⁢τ.(38)

[218.3.4] The resulting composite time evolution G⁢Tβ⁢ττ1⁢t⁢G⁢Tα⁢τ2τ2⁢t was studied in [53, 54] for the case β⁢τ=1. [218.3.5] Rescaling this composite operator as in the case of Debye relaxation and computing the infinitesimal generator yields the fractional differential equation [53, 54]

τ1⁢d⁢fd⁢t+τ2α⁢Aα⁢f=-f(39)

[page 219, §0]    with Aα from eq. (33) and inital value f⁢0=1. [219.0.1] Its solution is

f⁢t=E1,1-α,1⁢-tτ1,-τ2ατ1⁢t1-α(40)

where

Ea1,a2,b⁢z1,z2=∑k=0∞∑ℓ1≥0∑ℓ2≥0ℓ1+ℓ2=k⁢k!ℓ1!⁢ℓ2!⁢z1ℓ1⁢z2ℓ2Γ⁢b+a1⁢ℓ1+a2⁢ℓ2(41)

with a1,a2>0 and b,z1,z2∈C is the binomial Mittag-Leffler function [61].

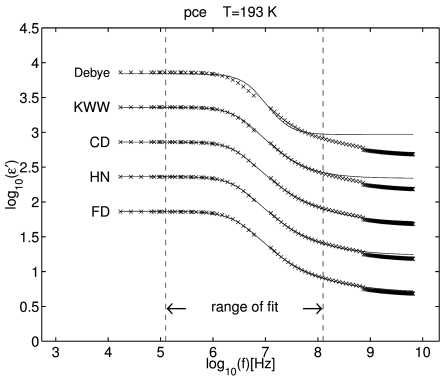
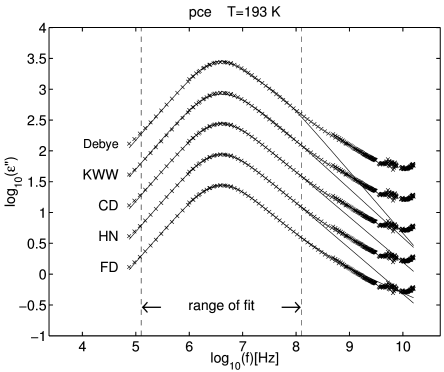
[page 220, §1]    [220.1.1] The complex frequency dependent susceptibility is obtained from the the normalized relaxation function as χ⁢u=1-u⁢f^⁢u where f^⁢u is the Laplace transform of f⁢t and u=i⁢ω is the imaginary circular frequency [54, p. 402, eq.(18)]. [220.1.2] The real part of the complex dielectric susceptibility for propylene carbonate at temperature T=193K is plotted in Figure 1, its imaginary part in Figure 2. [220.1.3] These figures are taken from [53]. [220.1.4] Crosses represent experimental data. [220.1.5] Different fit functions are shifted by half a decade for better visibility. [220.1.6] The range over which the data were fitted is indicated by two dashed vertical lines. [page 221, §0]    [221.0.1] The curve labelled FD (fractional dynamics) is the susceptibility corresponding to the relaxation function in eq. (40) It reproduces the high frequency wing even outside the range of its fit. [221.0.2] This is not the case for the other four curves curves, labelled Debye, KWW, CD and HN. They correspond to four popular fit functions for dielectric relaxation [55, 62]. [221.0.3] The curve Debye corresponds to a simple exponential function, KWW (Kohlrausch-Williams-Watts) is a stretched exponential relaxation function. [221.0.4] The relaxation functions for the two remaining cases, CD (Cole-Davison) and HN (Havriliak-Negami) were given for the first time in [58, 60].

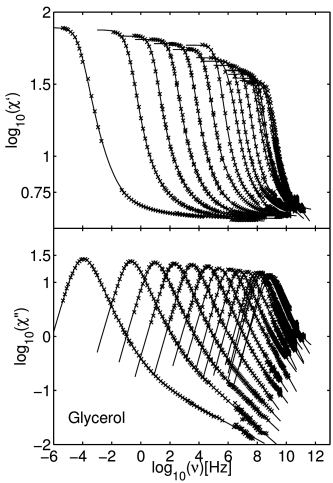
[221.1.1] Figure 3 from [54] shows the real and imaginary part of the dielectric susceptibility for glycerol as its temperature varies over the glass transition range from T=323K to T=184K. [221.1.2] The fits are based on a trinomial fractional relaxation function as detailed in [54, 61].

Figure 3: Separate fits for real part (upper figure) and imaginary part (lower figure) of the complex dielectric susceptibility χ⁢ν=χ′⁢ν+i⁢χ′′⁢ν of glycerol for temperatures T=323, 303, 295, 289, 273, 263, 253, 243, 234, 223, 213, 204, 195, 184 K (from right to left) as function of frequency ν (from [54]). The experimental data are taken from Ref. [56], the fit uses a generalized composite fractional relaxation model. For details see [54].