Sie sind hier: ICP » R. Hilfer » Publikationen

6 Representation of the solutions as functions of time

[1287.5.1] In [20] we obtained the analytical solution of a fractional differential equation of rational order, which we use to analyze our fitting results for model A and model B. [1287.5.2] For a general solution of equations (11) and (12) with arbitrary real αi see [35]. [1287.5.3] The restriction to rational αi is not a drawback, because we can approximate α1 and α2 by a rational value on a grid between 0 and 1. [1287.5.4] This number of grid points is chosen to be 20, which keeps computation times reasonably limited as the computing time increases quadratically with the lowest common denominator of α with 1.

[page 1288, §1]    [1288.1.1] The solution for f⁢t for model B is a sum of Mittag-Leffler type functions:

f⁢t=∑j=1NBj⁢∑k=0N-1cjN-k-1⁢E⁢-k/N,cjN;t,(14)

where N is the smallest number for which both α1⁢N and α2⁢N are integers. [1288.1.2] The coefficients cj are the zeros of the characteristic polynomial

cN+τ1α1⁢cα1⁢N+τ2α2⁢cα2⁢N+1=0,(15)

the function E⁢ν,a;t is defined as [36]

E⁢ν,a;t=tν⁢∑k=0∞a⁢tkΓ⁢ν+k+1.(16)

[1288.1.3] The coefficients Bj are the solutions of the linear system of equations

∑k=1Ncki⁢Bk=0,0≤i≤N-α1⁢N-1(17)
∑k=1Ncki+τ1α1⁢cki-N+α1⁢N⁢Bk=0,N-α1⁢N≤i≤N-α2⁢N-1(18)
∑k=1Ncki+τ1α1⁢cki-N+α1⁢N+τ2α2⁢cki-N+α2⁢N⁢Bk=0,N-α2⁢N≤i≤N-2.(19)

[1288.1.4] This solution is only valid if all the roots cj of the characteristic polynomial in (15) are distinct, which is checked in the computations. [1288.1.5] Because the linear system of equations (17)-(19) is underdetermined we choose one fundamental solution for Bj and a multiplication factor for f⁢t such that f⁢0=1.

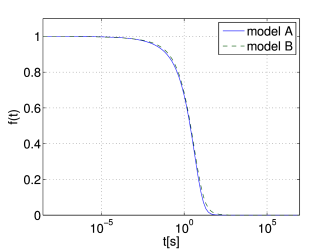
[page 1289, §1]    [1289.1.1] The analytical solutions are plotted for glycerol at 195⁢K (Fig. 7). [1289.1.2] The fitting values for τ for model A are τ1=4.991⁢s and τ2=1.089⁢s. [1289.1.3] Both values lie in the time interval where the relaxation occurs, which confirms the interpretation of these fitting parameters as relaxation times. [1289.1.4] For model B the fitted times are τ1=9.729⁢s and τ2=0.92⁢s. [1289.1.5] So τ2 marks the onset of the relaxation and τ1 the end.

Figure 7: The solutions of the fractional initial value problems (6) and (7) with f⁢0=1 using the fit parameters for model A and model B for glycerol at 195⁢K.

[1289.2.1] We note that the fractional derivatives appearing in the initial value problem (7) can be generalized to fractional derivatives of arbitrary type β introduced in [29] and defined as

D⁢fν,β⁢t=I⁢D1-β⁢ν-ν⁢Iν⁢fβ⁢ν-ν⁢t,0≤β≤1.(20)

[1289.2.2] For the case β=1 it reduces to the Riemann-Liouville fractional derivative, while for β=0 to the Liouville-Caputo-type derivative [33]. [1289.2.3] Because

D⁢E⁢μ,a;tν,β=D⁢E⁢μ,a;tν,γ,0≤β,γ≤1,μ>-1,ν≥0,(21)

the solution of our initial value problem does not change by replacing the Riemann-Liouville fractional derivatives with these generalized Riemann-Liouville fractional derivatives of type β.