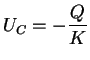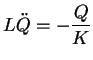Next: Literatur
Up: Einleitung
Previous: Werkzeuge oder ``Es geht
Neben der Benutzung fertiger Werkzeuge gibt es
eine weitere physikalische Methode um Programmierarbeit
zu vermeiden. Diese Methode beruht auf einer der wichtigsten
Grundtatsachen der Physik:
Ganz unterschiedliche physikalische Probleme können
auf ein und dasselbe mathematische Problem führen.
Dies hat folgende wichtige Konsequenz:
Hat man einmal ein mathematisches Problem numerisch
gelöst, so hat man häufig gleich eine ganze Reihe
von anderen physikalischen Problemen ebenfalls gelöst.
Wir wollen dies am Beispiel eines nichtmechanischen
harmonischen Oszillators, nämlich des elektrischen
Schwingkreises, verdeutlichen.
Elektrische Schwingkreise sind Grundbausteine
aller Fernseh- und Rundfunksender und -empfänger
und natürlich von Handy's und sonstigen
drahtlosen Kommunikationseinrichtungen.
Abbildung:
Schwingkreis
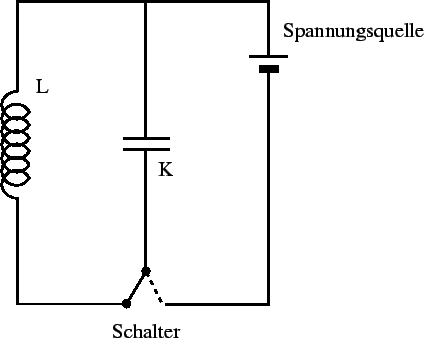 |
Ein elektrischer Schwingkreis besteht in seiner einfachsten
Form aus einer Spule und einem Kondensator, die in einem
Kreis geschaltet sind.
Die Auslenkung aus der Ruhelage beim Federpendel entspricht
hier der Aufladung des Kondensators durch eine angelegte
Gleichspannung
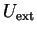 .
Im Anfangszustand (maximale elektrostatische Energie analog zur
potentiellen Energie) ist die Kondensatorspannung maximal; in der Spule
fliesst kein Strom. Beim Entladen des Kondensators baut der fliessende
Strom in der Spule ein magnetisches Feld auf (analog zur kinetischen Energie).
Ist der Kondensator entladen, analog zum Nulldurchgang des Pendels, so
nimmt das Magnetfeld wieder ab. Dadurch entsteht ein Strom, der den
Kondensator mit umgekehrter Spannung wieder auflädt.
.
Im Anfangszustand (maximale elektrostatische Energie analog zur
potentiellen Energie) ist die Kondensatorspannung maximal; in der Spule
fliesst kein Strom. Beim Entladen des Kondensators baut der fliessende
Strom in der Spule ein magnetisches Feld auf (analog zur kinetischen Energie).
Ist der Kondensator entladen, analog zum Nulldurchgang des Pendels, so
nimmt das Magnetfeld wieder ab. Dadurch entsteht ein Strom, der den
Kondensator mit umgekehrter Spannung wieder auflädt.
Da der Stromkreis geschlossen ist, müssen sich die Spannungen an der
Spule 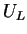 und Kondensator
und Kondensator 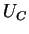 zu 0 addieren, d.h.
zu 0 addieren, d.h.
Nun ist der Spannungsabfall an der Spule (mit Lenzscher Regel)
wobei 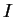 der elektrische Strom und
der elektrische Strom und 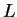 die Selbstinduktivität der Spule
ist.
Ausserdem lautet die Spannung am Kondensator
wobei
die Selbstinduktivität der Spule
ist.
Ausserdem lautet die Spannung am Kondensator
wobei 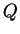 die Ladung am Kondensator und
die Ladung am Kondensator und 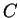 die Kapazität des Kondensators
ist. Sie ist der Spannung an der Spule entgegengerichtet.
Somit erhält man die Bewegungsgleichung
für die Ladung des Kondensators. Man erkennt, daß es sich dabei wieder um die Gleichung eines harmonischen Oszillators handelt. In Tabelle 1 sind die
einander entsprechenden Grössen dieser elektromechanischen Analogie
zusammengefasst. Die Lösung des mechanischen Problems bedeutet also
gleichzeitig die Lösung des elektrischen Problems.
die Kapazität des Kondensators
ist. Sie ist der Spannung an der Spule entgegengerichtet.
Somit erhält man die Bewegungsgleichung
für die Ladung des Kondensators. Man erkennt, daß es sich dabei wieder um die Gleichung eines harmonischen Oszillators handelt. In Tabelle 1 sind die
einander entsprechenden Grössen dieser elektromechanischen Analogie
zusammengefasst. Die Lösung des mechanischen Problems bedeutet also
gleichzeitig die Lösung des elektrischen Problems.
Tabelle 1: Elektromechanische Analogie
| Größe |
mech. |
elektr. |
| |
Federpendel |
Schwingkreis |
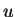 |
Auslenkung 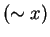 |
Ladung 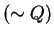 |
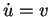 |
Geschwindigkeit |
Strom |
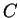 |
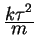 |
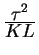 |




Next: Literatur
Up: Einleitung
Previous: Werkzeuge oder ``Es geht
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002

![]() und Kondensator
und Kondensator ![]() zu 0 addieren, d.h.
zu 0 addieren, d.h.