IV.A Examples
The present chapter begins the discussion of physical processes in porous media involving the transport or relaxation of physical quantities such as energy, momentum, mass or charge. As discussed in the introduction physical properties require equations of motion describing the underlying physical processes. Recurrent examples of experimental, theoretical and practical importance include :
-
the disordered diffusion equation
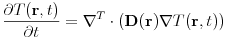
(4.1) where
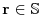 ,
, 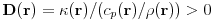 is the thermal diffusivity tensor,
is the thermal diffusivity tensor, 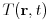 is the space time
dependent temperature field,
is the space time
dependent temperature field, 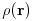 is the density,
is the density, 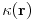 the thermal conductivity and
the thermal conductivity and 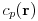 the specific heat at constant
pressure.
The superscript
the specific heat at constant
pressure.
The superscript 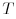 denotes transposition.
If the tensor field
denotes transposition.
If the tensor field 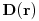 is sufficiently often differentiable
the equations are completed with boundary conditions at the sample
boundary
is sufficiently often differentiable
the equations are completed with boundary conditions at the sample
boundary 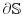 .
For the microscopic description of diffusion in a two component porous
medium
.
For the microscopic description of diffusion in a two component porous
medium 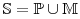 whose components have diffusivities
whose components have diffusivities
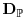 and
and 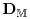 the diffusivity field
the diffusivity field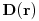 has the
form
has the
form ![{\bf D}({\bf r})={\bf D}_{\mathbb{P}}\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\bf r})+{\bf D}_{\mathbb{M}}\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{M}}}({\bf r})](mi/mi620.png) which is not differentiable at
which is not differentiable at  .
In such cases additional boundary conditions are required at the
internal interface
.
In such cases additional boundary conditions are required at the
internal interface  , and the equation is interpreted
in the sense of distributions [259].
Typical values for sedimentary rocks are
, and the equation is interpreted
in the sense of distributions [259].
Typical values for sedimentary rocks are
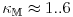 Wm
Wm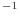 K
K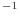 ,
,
![\rho\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{M}}}\approx 1..3](mi/mi607.png) g cm
g cm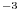 and
and 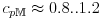 kJ kg
kJ kg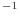 K
K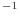 .
. -
the Laplace equation with variable coefficients
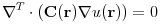
(4.2) where
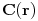 is again a second rank tensor field of local
transport coefficients,
is again a second rank tensor field of local
transport coefficients, 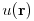 is a scalar field,
is a scalar field, 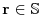 and the same remarks apply as for the diffusion equation
with respect to differentiability of
and the same remarks apply as for the diffusion equation
with respect to differentiability of 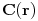 and boundary
conditions.
For constant
and boundary
conditions.
For constant 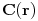 the equation reduces to the
Laplace equation
the equation reduces to the
Laplace equation 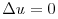 .
If the medium is random the coefficient matrix
.
If the medium is random the coefficient matrix 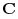 is a random function of
is a random function of 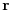 .
Equation (4.2) is the basic
equation for the next chapter.
It is frequently obtained as the steady state limit
of the timedependent equations such as the diffusion
equation (4.1).
Other examples of (4.2) occur in
fluid flow, dielectric relaxation, or dispersion in
porous media.
In dielectric relaxation
.
Equation (4.2) is the basic
equation for the next chapter.
It is frequently obtained as the steady state limit
of the timedependent equations such as the diffusion
equation (4.1).
Other examples of (4.2) occur in
fluid flow, dielectric relaxation, or dispersion in
porous media.
In dielectric relaxation 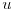 is the electric potential
and
is the electric potential
and 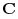 is the matrix of local (spatially varying)
dielectric permittivity. In diffusion problems or heat
flow
is the matrix of local (spatially varying)
dielectric permittivity. In diffusion problems or heat
flow 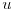 is the concentration field or temperature,
and
is the concentration field or temperature,
and 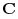 the local diffusivity. In Darcy flow through
porous media
the local diffusivity. In Darcy flow through
porous media 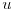 is the pressure and
is the pressure and 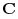 is the
tensor of locally varying absolute permeabilities.
is the
tensor of locally varying absolute permeabilities.
-
the elastic wave equation is a system of equations for the three components
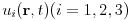 of a vector displacement field
of a vector displacement field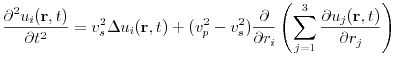
(4.3) where
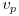 is the compressional and
is the compressional and 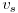 the shear wave
velocity of the material.
the shear wave
velocity of the material.
-
Maxwells equations in SI units for a medium with real dielectric constant
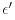 , magnetic permeability
, magnetic permeability 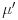 and real
conductivity
and real
conductivity 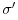 and charge density
and charge density 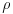
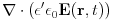

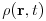
(4.4) 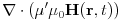

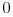
(4.5) 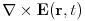

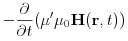
(4.6) 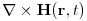

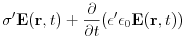
(4.7) for the electric field
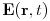 , magnetic field
, magnetic field 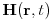 supplemented by boundary conditions and the continuity equation
supplemented by boundary conditions and the continuity equation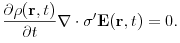
(4.8) Here
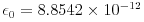 F/m is the permittivity
and
F/m is the permittivity
and 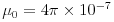 H/m is the magnetic permeability
of empty space.
H/m is the magnetic permeability
of empty space. -
the Navier-Stokes equations for the velocity field
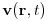 and the pressure field
and the pressure field 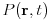 of an incompressible liquid flowing through
the pore space
of an incompressible liquid flowing through
the pore space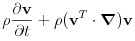

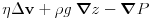
(4.9) 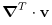

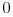
(4.10) where
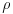 is the density and
is the density and 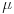 the viscosity of the
liquid.
The coordinate system was chosen such that the acceleration
of gravity
the viscosity of the
liquid.
The coordinate system was chosen such that the acceleration
of gravity 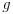 points in the
points in the 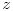 -direction.
These equations have to be supplemented with the no slip
boundary condition
-direction.
These equations have to be supplemented with the no slip
boundary condition 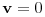 on the pore space boundary.
on the pore space boundary.
In the following mainly the equations for fluid transport and Maxwells equation for dielectric relaxation will be discussed in more detail. Combining fluid flow and diffusion into convection-diffusion equations yields the standard description for solute and contaminant transport [260, 261, 24, 262, 21, 26].
