Sie sind hier: ICP » R. Hilfer » Publikationen

3 Saturation Overshoot

3.1 Experimental Observations

[2328.2.1] Infiltration experiments [59] on constant flux imbibition into a very dry porous medium report existence of non-monotone travelling wave profiles for the saturation [55, 62]

S(z,t)=s(y) (20)

as a function of time t\geq 0 and position 0\leq z\leq 1 along the column. [2328.2.2] Here -\infty<y<\infty denotes the similarity variable

y=z-c^{*}t (21)

and the parameter -\infty<c^{*}<\infty is the constant wave velocity. [2328.2.3] From here on all quantitites z,t,y,S,c^{*} are dimensionless. [2328.2.4] The relation

\displaystyle\widehat{z}=zL (22a)

defines the dimensional depth coordinate 0\leq\widehat{z}\leq L increasing along the orientation of gravity. [2328.2.5] The length L is the system size (length of column). [2328.2.6] The dimensional time is

\displaystyle\widehat{t}=\frac{tL}{Q} (22b)

where Q denotes the total (i.e. wetting plus nonwetting) spatially constant flux through the column in m/s (see eq.  (13)). [2328.2.7] The dimensional similarity variable reads

\displaystyle\widehat{y}=yL=\widehat{z}-c^{*}Q\widehat{t}. (22c)

[2328.2.8] Experimental observations show fluctuating profiles with an overshoot region [59, 73, 54, 55, 74, 75]. [2328.2.9] It can be viewed as a travelling wave profile consisting of an imbibition front followed by a drainage front.

3.2 Mathematical Formulation in d=1

[2328.3.1] The problem is to determine the height S^{*} of the overshoot region (=tip) and its velocity c^{*} given an initial profile S(z,0), the outlet saturation S^{{\rm out}}, and the saturation S^{{\rm in}} at the inlet as data of the problem. [2328.3.2] Constant Q and constant S^{{\rm in}} are assumed for the boundary conditions at the left boundary. [2328.3.3] Note, that this differs from the experiment, where the flux of the wetting phase and the pressure of the nonwetting phase are controlled.

[2328.4.1] The leading (imbibition) front is a solution of the nondimensionalized fractional flow equation (obtained from eq.  (17) for d=1)

\phi\frac{\partial S}{\partial t}+\frac{\partial}{\partial z}\left[f_{{\mathrm{im}}}(S)-D_{{\mathrm{im}}}(S)\frac{\partial S}{\partial z}\right]=0 (23a)

[page 2329, §0]    while

\phi\frac{\partial S}{\partial t}+\frac{\partial}{\partial z}\left[f_{{\mathrm{dr}}}(S)-D_{{\mathrm{dr}}}(S)\frac{\partial S}{\partial z}\right]=0 (23b)

must be fulfilled at the trailing (drainage) front. [2329.0.1] Here \phi is the porosity and the variables z and t have been nondimensionalized using the system size L and the total flux Q. The latter is assumed to be constant. [2329.0.2] The functions f_{{\mathrm{im}}},f_{{\mathrm{dr}}} are the fractional flow functions for primary imbibition and secondary drainage. [2329.0.3] They are given as

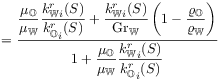\displaystyle f_{i}(S) \displaystyle=\frac{\displaystyle\frac{\mu _{{\mathbb{O}}}}{\mu _{{\mathbb{W}}}}\frac{{k^{r}_{{\mathbb{W}}}}_{i}(S)}{{k^{r}_{{\mathbb{O}}}}_{i}(S)}+\frac{{k^{r}_{{\mathbb{W}}}}_{i}(S)}{\mathrm{Gr}_{\mathbb{W}}}\left(1-\frac{\varrho _{{\mathbb{O}}}}{\varrho _{{\mathbb{W}}}}\right)}{\displaystyle 1+\frac{\mu _{{\mathbb{O}}}}{\mu _{{\mathbb{W}}}}\frac{{k^{r}_{{\mathbb{W}}}}_{i}(S)}{{k^{r}_{{\mathbb{O}}}}_{i}(S)}} (24a)
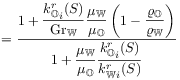\displaystyle=\frac{\displaystyle 1+\frac{{k^{r}_{{\mathbb{O}}}}_{i}(S)}{\mathrm{Gr}_{\mathbb{W}}}\frac{\mu _{{\mathbb{W}}}}{\mu _{{\mathbb{O}}}}\left(1-\frac{\varrho _{{\mathbb{O}}}}{\varrho _{{\mathbb{W}}}}\right)}{\displaystyle 1+\frac{\mu _{{\mathbb{W}}}}{\mu _{{\mathbb{O}}}}\frac{{k^{r}_{{\mathbb{O}}}}_{i}(S)}{{k^{r}_{{\mathbb{W}}}}_{i}(S)}} (24b)

with i\in\{{\mathrm{im}},{\mathrm{dr}}\} and the dimensionless gravity number [76, 37]

\displaystyle\mathrm{Gr}_{\mathbb{W}}=\frac{\mu _{{\mathbb{W}}}Q}{\varrho _{{\mathbb{W}}}gk} (25)

defined in terms of total flux Q, wetting viscosity \mu _{{\mathbb{W}}}, density \varrho _{{\mathbb{W}}}, acceleration of gravity g and absolute permeability k of the medium. [2329.0.4] The functions {k^{r}_{{\mathbb{W}}}}_{i}(S),{k^{r}_{{\mathbb{O}}}}_{i}(S) with i\in\{{\mathrm{im}},{\mathrm{dr}}\} are the relative permeabilities. [2329.0.5] The capillary flux functions for drainage and imbibition are defined as

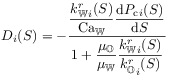D_{i}(S)=-\frac{\displaystyle\frac{{k^{r}_{{\mathbb{W}}}}_{i}(S)}{\mathrm{Ca}_{\mathbb{W}}}\frac{\mathrm{d}{{P_{\mathrm{c}}}}_{i}(S)}{\mathrm{d}S}}{\displaystyle 1+\frac{\mu _{{\mathbb{O}}}}{\mu _{{\mathbb{W}}}}\frac{{k^{r}_{{\mathbb{W}}}}_{i}(S)}{{k^{r}_{{\mathbb{O}}}}_{i}(S)}} (26)

with i\in\{{\mathrm{im}},{\mathrm{dr}}\} and a minus sign was introduced to make them positive. [2329.0.6] The functions {{P_{\mathrm{c}}}}_{i} are capillary pressure saturation relations for drainage and imbibition. [2329.0.7] The dimensionless number

\mathrm{Ca}_{\mathbb{W}}=\frac{\mu _{{\mathbb{W}}}QL}{{P_{{\rm b}}}k} (27)

is the macroscopic capillary number [76, 37] with {P_{{\rm b}}} representing a typical (mean) capillary pressure at S=0.5 (see eq.  (34)). [2329.0.8] For \mathrm{Ca}=\infty one has D_{i}=0 and eqs. (23) reduce to two nondimensionalized Buckley-Leverett equations

\phi\frac{\partial S}{\partial t}+\frac{\partial}{\partial z}f_{{\mathrm{im}}}(S)=0 (28a)

for the leading (imbibition) front and

\phi\frac{\partial S}{\partial t}+\frac{\partial}{\partial z}f_{{\mathrm{dr}}}(S)=0 (28b)

for the trailing (drainage) front.

[page 2330, §1]

3.3 Hysteresis

[2330.1.1] Conventional hysteresis models for the traditional theory require to store the process history for each location inside the sample [77, 78, 79]. [2330.1.2] Usually this means to store the pressure and saturation history (i.e. the reversal points, where the process switches between drainage and imbibition). [2330.1.3] A simple jump-type hysteresis model can be formulated locally in time based on eq.  (23) as

\phi\frac{\partial S}{\partial t}+\Xi(S)\frac{\partial}{\partial z}\left[f_{{\mathrm{im}}}(S)-D_{{\mathrm{im}}}(S)\frac{\partial S}{\partial z}\right]+\left[1-\Xi(S)\right]\frac{\partial}{\partial z}\left[f_{{\mathrm{dr}}}(S)-D_{{\mathrm{dr}}}(S)\frac{\partial S}{\partial z}\right]=0. (29)

[2330.1.4] Here \Xi(S) denotes the left sided limit

\Xi(S)=\lim _{{\varepsilon\to 0}}\mathrm{\Theta}\left[\frac{\partial S}{\partial t}(z,t-\varepsilon)\right], (30)

\mathrm{\Theta}(x) is the Heaviside step function (see eq.  (35)), and the parameter functions f_{i}(S),D_{i}(S) with i\in\{{\mathrm{dr}},{\mathrm{im}}\} require a pair of capillary pressure and two pairs of relative permeability functions as input. [2330.1.5] The relative permeability functions employed for computations are of van Genuchten form [80, 81]

\displaystyle{k^{r}_{{\mathbb{W}}}}_{i}({S_{{e}}}_{i}) \displaystyle={K^{e}_{\mathbb{W}}}_{i}{S_{{e}}}_{i}^{{1/2}}\left[1-(1-{S_{{e}}}_{i}^{{1/\alpha _{i}}})^{{\alpha _{i}}}\right]^{2} (31a)
\displaystyle{k^{r}_{{\mathbb{O}}}}_{i}({S_{{e}}}_{i}) \displaystyle={K^{e}_{\mathbb{O}}}_{i}(1-{S_{{e}}}_{i})^{{1/2}}(1-{S_{{e}}}_{i}^{{1/\beta _{i}}})^{{2\beta _{i}}} (31b)

with i\in\{{\mathrm{im}},{\mathrm{dr}}\} and

{S_{{e}}}_{i}(S)=\frac{S-{S_{{\mathbb{W}\rm i}}}^{i}}{1-{S_{{\mathbb{O}\rm r}}}^{i}-{S_{{\mathbb{W}\rm i}}}^{i}} (32)

the effective saturation. [2330.1.6] The resulting fractional flow functions with parameters from Table 1 are shown in Figure 1b. [2330.1.7] The capillary pressure functions used in the computations are

{P_{\mathrm{c}}}_{i}({S_{{e}}}_{i})={P_{{\rm b}}}_{i}\left({S_{{e}}}_{i}^{{-1/\alpha _{i}}}-1\right)^{{1-\alpha _{i}}} (33)

with i={\mathrm{dr}},{\mathrm{im}} and the typical pressure {P_{{\rm b}}} in (27) is defined as

{P_{{\rm b}}}=\frac{{P_{\mathrm{c}}}_{{\mathrm{im}}}(0.5)+{P_{\mathrm{c}}}_{{\mathrm{dr}}}(0.5)}{2}. (34)

[2330.1.8] Equation (29) with initial and boundary conditions for S and an initial condition for \partial S/\partial t is conjectured to be a well defined semigroup of bounded operators on L^{1}([0,L]) on a finite interval [0,T] of time. [2330.1.9] The conjecture is supported by the fact that each of the equations (23) individually defines such a semigroup, and because multiplication by \Xi or (1-\Xi) are projection operators.