4 Approximate Analytical Solution
4.1 Step Function Approximation
[2330.2.1] The basic idea of the analysis below
is to approximate the travelling wave profile
for long times ![]() with piecewise constant functions (step functions).
[2330.2.2] For large
[page 2331, §0]
with piecewise constant functions (step functions).
[2330.2.2] For large
[page 2331, §0]
![]() (i.e. in the Buckley-Leverett limit) one may
view this approximate profile as a superposition of two
Buckley-Leverett shock fronts.
[2331.0.1] This is possible by virtue of the fact, that the Heaviside step
function
(i.e. in the Buckley-Leverett limit) one may
view this approximate profile as a superposition of two
Buckley-Leverett shock fronts.
[2331.0.1] This is possible by virtue of the fact, that the Heaviside step
function
| (35) |
can also be regarded as a function of the similarity
variable ![]() of the Buckley-Leverett problem.
of the Buckley-Leverett problem.
[2331.1.1] In the crudest approximation
one can split the total profile
for sufficiently large ![]() into the sum
into the sum
| (36a) | |
of an imbibition front
| (36b) | |
located at ![]() and a drainage front profile located at
and a drainage front profile located at ![]()
| (36c) | |
both moving with the same speed ![]() ,
where
,
where ![]() resp.
resp. ![]() are the upper
(inlet) resp.
lower (outlet) saturations and
are the upper
(inlet) resp.
lower (outlet) saturations and ![]() is the maximum (overshoot) saturation.
[2331.1.2] The quantity
is the maximum (overshoot) saturation.
[2331.1.2] The quantity ![]() is the distance by which the imbibition
front precedes the drainage front, i.e. the width of the tip
(=overshoot) region.
is the distance by which the imbibition
front precedes the drainage front, i.e. the width of the tip
(=overshoot) region.
4.2 Travelling wave solutions
[2331.2.1] The two equations (28) become coupled,
if eq. (20) holds true, because
then there is only a single wave speed ![]() for both fronts.
[2331.2.2] At the imbibition discontinuity
the Rankine-Hugoniot condition demands
for both fronts.
[2331.2.2] At the imbibition discontinuity
the Rankine-Hugoniot condition demands
| (37a) | |
and the second equality (with colon)
defines the function ![]() .
[2331.2.3] Similarly
.
[2331.2.3] Similarly
| (37b) | |
defines the drainage front velocity as a function
![]() of the overshoot
of the overshoot ![]() .
Examples of the velocities
.
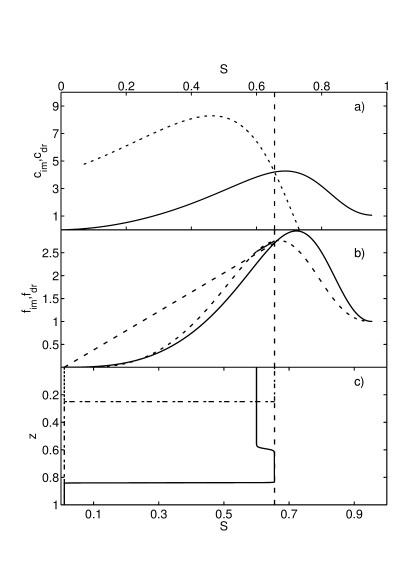
Examples of the velocities ![]() used in the compuations are
shown in Figure 1a.
[2331.2.4] For a travelling wave both fronts move with the same velocity so that
the mathematical problem is to find a solution
used in the compuations are
shown in Figure 1a.
[2331.2.4] For a travelling wave both fronts move with the same velocity so that
the mathematical problem is to find a solution ![]() of the equation
of the equation
| (38) |
obtained from equating eqs. (37b) and (37a)
(See Fig. 1a).
[2331.2.5] The wave velocity ![]() is then obtained as
is then obtained as ![]() or equivalently as
or equivalently as ![]() .
.
[page 2332, §1]
4.3 General overshoot solutions with two wave speeds
[2332.1.1] Equation (38) provides a necessary condition for
the existence of a travelling wave solution of the form of
eq. (36) with velocity ![]() and overshoot
and overshoot ![]() .
[2332.1.2] More generally, if the saturation plateau
.
[2332.1.2] More generally, if the saturation plateau ![]() is larger or
smaller than
is larger or
smaller than ![]() , one expects to find non-monotone profiles
that are, however, not travelling waves.
[2332.1.3] Instead the drainage
and imbibition fronts are expected to
have different velocities.
[2332.1.4] The fractional flow functions with relative permeabilities
from eqs. (31)
and the parameters from Table 1 give
for
, one expects to find non-monotone profiles
that are, however, not travelling waves.
[2332.1.3] Instead the drainage
and imbibition fronts are expected to
have different velocities.
[2332.1.4] The fractional flow functions with relative permeabilities
from eqs. (31)
and the parameters from Table 1 give
for ![]() the result
the result
| (39) |
while for ![]() one has
one has
| (40) |
[2332.1.5] In this case, for plateau saturations ![]() , the
leading (imbibition) front has a smaller velocity than
the trailing (drainage) front.
[2332.1.6] Thus the trailing front catches up and
the profile approaches a single front at long times.
[2332.1.7] For plateau saturations
, the
leading (imbibition) front has a smaller velocity than
the trailing (drainage) front.
[2332.1.6] Thus the trailing front catches up and
the profile approaches a single front at long times.
[2332.1.7] For plateau saturations ![]() on the other hand the trailing
drainage front moves slower than the leading imbibition front.
[2332.1.8] In this case a non-monotone profile persists indefinitely, albeit
with a plateau (tip) width that increases linearly with
time.
on the other hand the trailing
drainage front moves slower than the leading imbibition front.
[2332.1.8] In this case a non-monotone profile persists indefinitely, albeit
with a plateau (tip) width that increases linearly with
time.
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| system size | 1.0 | m | |
| porosity | 0.38 | – | |
| permeability | m |
||
| density |
1000 | kg/m |
|
| density |
800 | kg/m |
|
| viscosity |
0.001 | Pa |
|
| viscosity |
0.0003 | Pa |
|
| imbibition exp. | 0.85 | – | |
| drainage exp. | 0.98 | – | |
| end pnt. rel.p. | 0.35 | – | |
| end pnt. rel.p. | 1 | – | |
| end pnt. rel.p. | 0.35 | – | |
| end pnt. rel.p. | 0.75 | – | |
| imb. cap. press. | 55.55 | Pa | |
| dr. cap. press. | 100 | Pa | |
| end pnt. sat. | 0 | – | |
| end pnt. sat. | 0.07 | – | |
| end pnt. sat. | 0.045 | – | |
| end pnt. sat. | 0.045 | – | |
| boundary sat. | 0.01 | – | |
| boundary sat. | 0.60 | – | |
| total flux | 1.196 10 |
m/s |
