Sie sind hier: ICP » R. Hilfer » Publikationen

3 Averaged Induced Dynamics in the Ultralong Time Limit

[552.1.1]The induced transformations \widetilde{S}_{G} and S_{G} were defined for discrete time, and it is of interest to remove the discretization to obtain the induced dynamics in continuous time. [552.1.2]The conventional view on discrete vs. continuous time in ergodic theory assumes 0<\Delta t<\infty for the discretization time step, and holds that “there is no essential difference between discrete-time and continuous-time systems”[24],page 51. 1 (This is a footnote:) 1 It is argued that one can always write t\in\mathbb{R} as t=\epsilon+n\Delta t where \epsilon=t-n\Delta t is small and n=[t/\Delta t] is the largest integer not larger than t/\Delta t. As long as 0<\Delta t<\infty the continuous long time limit \lim _{{t\rightarrow\infty}}\widetilde{T}^{t} corresponds to the discrete long time limit \lim _{{k\rightarrow\infty}}\widetilde{T}^{{k\Delta t}}. [552.1.3]Obviously, this equivalence between discrete and continuous time breaks down for induced dynamics because the continuous flow of time within G is interrupted by time periods of fluctuating length during which the trajectory wanders outside G. [552.1.4]These interruptions produce a discontinuous (fluctuating) flow of time.

[552.2.1]There are three possibilities for removing the discretization using a long time limit. [552.2.2]Only one of these employs the conventional assumption 0<\Delta t<\infty (or \Delta t=1). [552.2.3]The two other alternatives are \Delta t\rightarrow 0 and \Delta t\rightarrow\infty. [552.2.4]The first alternative considers the limit \lim _{{\Delta t\rightarrow 0,k\rightarrow\infty}}\widetilde{S}^{{k\Delta t}} in which the discretization step becomes small. [552.2.5]This possibility may be called the short-long-time limit or continuous time limit, and it was discussed in [21]. [552.2.6]The second alternative is to consider the limit \lim _{{\Delta t\rightarrow\infty,k\rightarrow\infty}}\widetilde{S}^{{k\Delta t}} in which the discretization step diverges \Delta t\rightarrow\infty. [552.2.7]This will be considered in this paper, and it is called the long-long-time limit or the ultralong-time limit. [552.2.8]These limits are analogous to the ensemble limit [18, 19, 20, 21].

[552.3.1]According to its definition (8) the induced time transformation S_{G} acts as a convolution operator in time

S_{G}\varrho(B)=\varrho(B)*p. (9)

[552.3.2]Applying the transformation N times yields

S_{G}^{N}\varrho(B)=(S_{G}^{{N-1}}\varrho(B))*p=\varrho(B)*\;\underbrace{p*...*p}_{{N\;\;{\rm factors}}}=\varrho(B)*p_{N} (10)

[page 553, §0]   where the last equation defines the N-fold convolution p_{N}(k). [553.0.1]If p_{\infty}=\lim _{{N\rightarrow\infty}}p_{N} exists this defines also S_{G}^{N} in the N\rightarrow\infty long time limit.

[553.1.1]To determine whether a limiting density p_{\infty} exists, note that the N-fold convolution p_{N}(k)=p(k)*...*p(k) gives the probability density p_{N}(k)=Prob\{\mathcal{T}_{N}=k\Delta t\} of the random variable \mathcal{T}_{N}=\tau _{1}+...+\tau _{N} representing the sum of N independent and identically distributed random recurrence times \tau _{j} with common lattice distribution p(k)=p_{1}(k). [553.1.2]A necessary and sufficient condition for the existence of a limiting density p_{\infty} for suitably renormalized recurrence times is that the discrete lattice probability density p(k) belongs to the domain of attraction of a stable density [25, 26]. [553.1.3]Then, because \Delta t is defined as the maximal value such that all the \tau _{i} are concentrated on the arithmetic progression k\Delta t, it follows that for a suitable choice of renormalization constants C_{N},D_{N}

\lim _{{N\rightarrow\infty}}\sup _{{k}}\left|\frac{D_{N}}{\Delta t}p_{N}(k)-h\left(\frac{k\Delta t-C_{N}}{D_{N}};\varpi,\zeta,C,D\right)\right|=0 (11)

where h(x;\varpi,\zeta,C,D) is a limiting stable density whose parameters obey 0<\varpi\leq 2, -1\leq\zeta\leq 1, -\infty<C<\infty, and D\geq 0 [25, 26, 27]. [553.1.4]If D=0 then the limiting distribution is degenerate, h(x;\varpi,\zeta,C,0)=\delta(x-C) for all values of \varpi,\zeta.

[553.2.1]The positivity of the recurrence times \tau _{i}\geq 0 for all i\in\mathbb{N} implies that the renormalized recurrence times \mathcal{T}_{N} are bounded below, and this gives rise to the constraint P_{\infty}(t)=0 for t\leq C on the possible limiting distributions. [553.2.2]The limiting stable distributions compatible with this constraint are given by those with parameters 0<\varpi\leq 1 and \zeta=-1. [553.2.3]For 0<\varpi<1 the limiting densities may be abbreviated as

h(x;\varpi,-1,C,D)=\frac{1}{D^{{1/\varpi}}}h_{\varpi}\left(\frac{t-C}{D^{{1/\varpi}}}\right) (12)

which expresses the well known scaling relations for stable distributions [25, 26, 18, 20]. [553.2.4]The scaling function h_{\varpi}(x) can be expressed explicitly as

h_{\varpi}(x)=\frac{1}{x\varpi}H^{{10}}_{{11}}\left(\frac{1}{x}\right.\left|\begin{array}[]{c}(0,1)\\ (0,1/\varpi)\end{array}\right) (13)

in terms of general H-functions whose definition may be found in [28] or [18, 20]. [553.2.5]For \varpi=1 one finds

h_{1}(x)=\lim _{{\varpi\rightarrow 1^{-}}}h_{\varpi}(x)=\delta(x-1) (14)

the Dirac distribution concentrated at x=1 as the limiting density. [553.2.6]If the limit exists and is nondegenerate, i.e D\neq 0, the renormalization constants D_{N} must have the form

D_{N}=(N\Lambda(N))^{{1/\varpi _{X}}} (15)

where \Lambda(N) is a slowly varying function [26], defined by the condition that

\lim _{{x\rightarrow\infty}}\frac{\Lambda(bx)}{\Lambda(x)}=1 (16)

for all b>0.

[553.3.1]Using equations (11) and (12) one has for N\rightarrow\infty

p_{N}(k)\approx\frac{\Delta t}{D_{N}}h\left(\frac{k\Delta t-C_{N}}{D_{N}};\varpi,-1,C,D\right)=\frac{\Delta t}{D_{N}D^{{1/\varpi}}}h_{\varpi}\left(\frac{k\Delta t}{D_{N}D^{{1/\varpi}}}\right) (17)

[page 554, §0]   where the centering constants have been chosen conveniently as C_{N}=-CD_{N}. [554.0.1]From this it is clear that the traditional long time limit N\rightarrow\infty keeping 0<\Delta t<\infty finite produces \lim _{{{N\rightarrow\infty}\atop{0<\Delta t<\infty}}}k\Delta t/(DN\Lambda(N))^{{1/\varpi}}=0 for k finite, and thus \lim _{{{N\rightarrow\infty}\atop{0<\Delta t<\infty}}}p_{N}(k)=0, unless D=0. [554.0.2]Therefore the conventional long time limit produces a degenerate limiting distribution if it exists. [554.0.3]The ultralong time limit on the other hand allows \Delta t to become infinite. [554.0.4]If \Delta t diverges such that

\lim _{{{N\rightarrow\infty}\atop{\Delta t\rightarrow\infty}}}\frac{k\Delta t}{D_{N}}=t (18)

exists, then this defines a renormalized ultralong continuous time, 0<t<\infty. [554.0.5]In this case D>0 contrary to the conventional limit. [554.0.6]It follows that \lim _{{{N\rightarrow\infty}\atop{\Delta t\rightarrow\infty}}}kp_{N}(k)=th_{\varpi}(t/D^{{1/\varpi}})/D^{{1/\varpi}} and thus from eq. (10) that

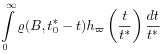\displaystyle S^{{t^{*}}}_{\varpi}\varrho(B,t_{0}^{*}) \displaystyle= \displaystyle\int\limits _{0}^{\infty}\varrho(B,t_{0}^{*}-t)h_{\varpi}\left(\frac{t}{t^{*}}\right)\frac{dt}{t^{*}} (19)
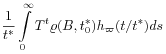\displaystyle= \displaystyle\frac{1}{t^{*}}\int\limits _{0}^{\infty}T^{t}\varrho(B,t_{0}^{*})h_{\varpi}(t/t^{*})ds

where the ultralong time parameter t^{*} was identified as

t^{*}=D^{{1/\varpi}}>0. (20)

[554.0.7]The identification of t^{*} is justified for two reasons. [554.0.8]On the one hand D\propto\langle|\tau-\tau^{\prime}|^{\sigma}\rangle^{{\varpi/\sigma}} for all \sigma<\varpi, where \langle...\rangle is the expectation with respect to the limiting distribution, and \tau,\tau^{\prime} are two independent random recurrence times. [554.0.9]This shows that D^{{1/\varpi}} has dimensions of time. [554.0.10]Secondly for \varpi=1 it follows from (14) that

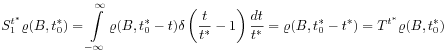S^{{t^{*}}}_{1}\varrho(B,t_{0}^{*})=\int\limits _{{-\infty}}^{\infty}\varrho(B,t_{0}^{*}-t)\delta\left(\frac{t}{t^{*}}-1\right)\frac{dt}{t^{*}}=\varrho(B,t_{0}^{*}-t^{*})=T^{{t^{*}}}\varrho(B,t_{0}^{*}) (21)

which again identifies t^{*}=D^{{1/\varpi}} as an ultralong time parameter. [554.0.11]Note that the results (19) and (21) imply macroscopic (=ultralong time) irreversibility by virtue of (20) even if the underlying time evolution \widetilde{T}^{t} resp. [554.0.12]T^{t} was reversible. [554.0.13]Perhaps this could provide new insight into the longstanding irreversibility paradox. [554.0.14]The fundamental convolution semigroup (19) was first obtained in [18, 19] and [21].