Sie sind hier: ICP » R. Hilfer » Publikationen

4 Fractional Stationarity

[554.1.1]This section investigates the condition of invariance or stationarity for the induced ultralong time dynamics S^{{t^{*}}}_{\varpi}. [554.1.2]Invariance of a measure \nu on G under the induced dynamics S^{{t^{*}}}_{\varpi} is defined as usual (see (3)) by requiring that

S^{{t^{*}}}_{\varpi}\nu(B,t_{0}^{*})=\nu(B,t_{0}^{*}) (22)

for t>0 and B\subset G. [554.1.3]For 0<\varpi<1 (22) may be called the condition of fractional invariance or fractional stationarity. [554.1.4]Using (2) the invariance condition becomes

A_{\varpi}\nu(B,t)=0 (23)

[page 555, §0]   for t>0 where A_{\varpi} is the infinitesimal generator of the semigroup S^{{t^{*}}}_{\varpi}. [555.0.1]For \varpi=1 the relation (21) implies A_{1}\nu(B,t)=-d\nu(B,t)/dt=0, and thus in this case invariant measures conserve volumes in phase space as usual. [555.0.2]A very different situation arises for \varpi<1.

[555.1.1]For 0<\varpi<1 the infinitesimal generators of the stable convolution semigroup S^{{t^{*}}}_{\varpi} are obtained [26] by evaluating the generalized function s_{+}^{{-\varpi-1}} [29] on the time translation group T^{s}

A_{\varpi}\varrho(t)=c^{+}\int _{0}^{\infty}s^{{-\varpi-1}}(T^{s}-T^{0})\, ds\,\varrho(t)=c^{+}\int _{0}^{\infty}s_{+}^{{-\varpi-1}}T^{s}\, ds\,\varrho(t) (24)

where c^{+}>0 is a constant. [555.1.2]Comparing (24) with the Balakrishnan algorithm [30, 31, 32] for fractional powers of the generator of a semigroup T^{t}

\displaystyle(-A)^{\alpha}\varrho(t) \displaystyle= \displaystyle\lim _{{t\rightarrow 0^{+}}}\left(\frac{I-T^{t}}{t}\right)^{\alpha}\varrho (25)
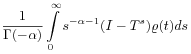\displaystyle= \displaystyle\frac{1}{\Gamma(-\alpha)}\int\limits _{0}^{\infty}s^{{-\alpha-1}}(I-T^{s})\varrho(t)ds

shows that if A=-d/dt denotes the infinitesimal generator of the original time evolution T^{t} then A_{\varpi}=(-A)^{\varpi} is the infinitesimal generator of the induced time evolution S^{{t^{*}}}_{\varpi}. [555.1.3]For 0<\varpi<1 the generators A_{\varpi} for S_{\varpi}^{{t^{*}}} are fractional time derivatives [15, 31, 29]. [555.1.4]The differential form (23) of the fractional invariance condition for \nu becomes

\frac{d^{\varpi}}{dt^{\varpi}}\nu(B,t)=0 (26)

for t>0 which was first derived in [18, 19]. [555.1.5]Its solution is

\nu(B,t)=C_{0}t^{{\varpi-1}} (27)

for t>0 with C_{0} a constant. [555.1.6]This shows that \nu(B) for a fractional stationary dynamical state is not constant. [555.1.7]Fractional stationarity or fractional invariance of a measure \nu implies that phase space volumes \nu(B) shrink with time. [555.1.8]Thus fractional dynamics is dissipative. [555.1.9]More generally (26) reads A_{\varpi}\nu(B,t)=\delta(t) with solution \nu(B,t)=C_{0}t_{+}^{{\varpi-1}} for t\geq 0 in the sense of distributions. [555.1.10]The stationary solution with \varpi=1 has a jump discontinuity at t=0, and is not simply constant.

[555.2.1]The transition from an original invariant measure \mu on \Gamma to a fractional invariant measure \nu on a subset G of measure \mu(G)=0 may be called stationarity breaking. [555.2.2]It occurs spontaneously in the sense that it is generated by the dynamics itself. [555.2.3]Stationarity breaking implies ergodicity breaking, and thus the ultralong time limit is a possible scenario for ergodicity breaking in ergodic theory.

[555.3.1]The present paper has shown that the use of fractional time derivatives in physics is not only justified, but arises generically for induced dynamics in the ultralong time limit. [555.3.2]This mathematical result applies to many physical situations. [555.3.3]In the simplest case the resulting fractional differential equation (26) defines fractional stationarity which provides the dynamical basis for the anequilibrium concept [18]. [555.3.4]Recently fractional random walks were discussed [8] and solved [10] in the continuum limit.

[page 556, §0]   ACKNOWLEDGEMENT : The author is grateful to Norges Forskningsrad (Nr.: 424.94 / 004 B) for financial support.