Article

[p. 398l, §1]
The upsurge of fractal models in the study of transport properties of disordered materials poses the question whether the Einstein relation whose derivation depends on spatial homogeneity is also valid for fractals or other inhomogeneous structures [1, 2]. Recently a general probabilistic analogue of the Einstein relation as a connection between mean first-passage times and passage probabilities in general Markov chains was identified [3, 4]. Here we present a more compact derivation.

[p. 398l, §2]
We will start with a simple probabilistic argument for the basic relation. We then interpret the result and apply it to finitely ramified fractals. Form these considerations we obtain the so-called fractal Einstein relation [5]. Finally, we use mean-first-passage times to give the star-triangle transformation for Markov chains and calculate exactly the fracton (spectral) dimension of fractal trees. We emphasize the relevance of our results for simulation and experiment.

[p. 398l, §3]
Let us begin by presenting a simple connection between first-passage times and first-passage probabilities in a finite-dimensional Markov chain. A finite-dimensional Markov chain can be visualized as a walker (or particle) moving randomly between a finite number of states (sites). The transitions of the walker from site $i$ to site $j$ are governed by a transition matrix $W$ whose elements $\omega _{{ij}}$ give the single-step transition probabilities. For simplicity we assume the chain to be ergodic, i. e., for every pair of sites $i,\, j$ there is a minimal integer $n$ such that $(W^{n})_{{ij}}>0$ . Thus, after sufficiently long times, the chain reaches stationarity where every state has a nonzero dwelling probability. Our objective is now to describe the spatiotemporal behavior by studying the transitions between two predetermined states.

[p. 398l, §4]
Let $T_{{0b}}(t)$ denote the probability density that a walker starting form site $0$ at time $t=0$ will reach the site $b$ (boundary) ^a (This is a footnote:) ^aBy a suitable modification of the Markov chain $T_{{0b}}$ can also describe transistions between subsets of points. for the first time after time $t$ . Let $T^{\prime}_{{0b}}(t)$ be the conditional probability density for first reaching $b$ after a time $t$ under the restriction that the starting point $0$ is not visited. Let the density $T_{{00}}(t)$ describe the regeneration time between two visits to the point $0$ . Analogously, $T^{\prime}_{{00}}(t)$ is the first-passage-time density from $0$ to $0$ conditioned on not reaching $b$ . We call $p$ the conditional probability that the walker after starting at $0$ returns to $0$ without having visited $b$ . With probability $q=1-p$ the walker passes directly form $0$ to $b$ without ever returning to $0$ . In Markov chain theory $q$ is called the harmonic measure relative to the boundary $b$ .

[p. 398r, §5]
The probability density $T_{{0b}}(t)$ governing the time between start at $0$ and the first visit to $b$ consists of two parts. With probability $p$ the walker will visit its starting point $0$ for a second or third time before reaching $b$ . Upon such a visit he starts anew because of the Markov property. Therefore, in this case the random transition time is the sum of the random time for conditional regeneration governed by $T^{\prime}_{{00}}(t)$ and the unconditioned first-passage time $T_{{0b}}(t)$ . On the other hand, the walker manages with probability $q$ to pass directly to site $b$ without revisiting $0$ . Thence, we find

$T_{{0b}}(t)=pT^{\prime}_{{00}}(t)\ast T_{{0b}}(t)+qT^{\prime}_{{0b}}(t),$

(1a)

where $\ast$ denotes convolution as is appropiate for sums of random variables. Analogously a regeneration at the origin takes place either without visiting $b$ or via a direct visit to $b$ and a subsequent transition from $b$ to $0$ . That implies a second relation,

$T_{{00}}(t)=pT^{\prime}_{{00}}(t)+qT^{\prime}_{{0b}}(t)\ast T_{{b0}}(t).$

(1b)

Laplace transforming equations (1a) und (1b) we obtain

$\displaystyle T_{{0b}}(u)$	$\displaystyle=pT^{\prime}_{{00}}(u)T_{{0b}}(u)+qT^{\prime}_{{0b}}(u),$		(2a)
$\displaystyle T_{{00}}(u)$	$\displaystyle=pT^{\prime}_{{00}}(u)+qT^{\prime}_{{0b}}(u)T_{{b0}}(u).$		(2b)

Inserting $qT^{\prime}_{{0b}}$ from eq. (2a) into (2b) yields

$pT^{\prime}_{{00}}(u)=\frac{T_{{00}}(u)-T_{{0b}}(u)T_{{b0}}(u)}{1-T_{{0b}}(u)T_{{b0}}(u)}.$

(3)

In the limit $u\rightarrow 0$ we get, using $T(0)=1$ and

[p. 399l, §0]

$-\frac{d}{du}T(u)\mid _{{u=0}}=\langle T\rangle,$

the desired result for the mean-first-passage times $\langle T\rangle$ ,

$\langle T_{{00}}\rangle=q\big[\langle T_{{0b}}\rangle+\langle T_{{b0}}\rangle\big].$

(4)

[p. 399l, §1]
This relation may be visualized as follows. One out of $1/q$ walkers will arrive at $b$ without having revisited $0$ . Therefore, launching successively walkers form $0$ , one has to wait on the average $1/q$ times the mean regeneration time $\langle T_{{00}}\rangle$ until one of them will return who has reached the prescribed point $b$ .

[p. 399l, §2]
We now argue that eq. (4) is indeed a probabilistic analogue of the Einstein relation. It is furthermore a generalization in the sense that it is valid for arbitrary inhomogeneous (including fractal) geometries. For this to be valid we have to identify the quantities analogous to the diffusion constant and the conductivity.

[p. 399l, §3]
To identify the diffusion constant we note that the relation $\langle r^{2}(t)\rangle\propto t$ for the mean square displacement of a random walk in Euclidean space is also valid in the form $\langle t(r)\rangle\propto r^{2}$ . Here $\langle t(r)\rangle$ is the mean first-exit time for the random walk to leave a sphere of radius $r$ around its starting point [6]. This is a consequence of the invariance of the Wiener process under the transformation $t\mapsto b^{2}t,\, r\mapsto br$ with $b>0$ . If $r(t)$ is a realization of the random process then also $r^{\prime}(t)=br(t/b^{2})$ is a realization. Thus, the time $t_{1}$ when $r(t)$ exits for the first time a sphere of radius $1$ around its origin defines also the first-exit time $t^{\prime}_{1}=b^{2}t_{1}$ for the scaled trajectory and a sphere of radius $b$ . It follows that the mean-first-exit time scales as $\langle t(b)\rangle\propto b^{2}$ in regular geometries. With this in mind we can thus take $D(L)\equiv L^{2}/\langle T(L)\rangle$ as the definition of a generalized scale-dependent diffusion coefficient in an arbitrary inhomogeneous structure of linear dimension $L$ .

[p. 399l, §4]
To identify the conductivity we have to look at a different physical situation. We need to introduce an external potential into our random-walk picture. This is done by assuming that the walker has a probability $\rho$ of being absorbed at $b$ and subsequently being replaced at site $0$ . This “voltage source” between $0$ and $b$ will establish a probability current depending on the magnitude of the “potential” $\rho$ . If $N$ walkers are starting from the origin then $Nq$ of them will reach $b$ without having returned to $0$ . On the average there will be

$n=Nq\rho$

(5)

walkers passing through the voltage source between $b$ and $0$ . In equilibrium the probability current is thus equal to $n/N$ and we recognize (5) as Ohm’s law if $q$ interpreted as the conductance. For a system of linear dimension $L$ and cross section $A$ the probabilistic conductivity is then defined as $\sigma=qL/A$ . This identifies the probability $q$ as the essential quantity for the conductivity.

[p. 399l, §5]
We can now return to the pure-random-walk picture without external potential. Assuming $\langle T_{{0b}}\rangle=\langle T_{{b0}}\rangle$ for the mean-first-passage time to the boundary at a distance $L$ form the starting point $0$ we get from eq. (4)

$\langle T_{{00}}\rangle=2\sigma V\langle T_{{0b}}\rangle/L^{2}\propto L^{2}2\sigma V/D,$

where $V$ is the corresponding volume. We remember that $\langle T_{{00}}\rangle$ is the stationary regeneration time (in the absence of the external potential) and hence independent of $\rho$ . We thus arrive at the Einstein relation $\sigma\propto D$ . Independent of us, Gefen and Goldhirsch [7] have recently developed a similar picture.

[p. 399r, §6]
We proceed to apply this result to a fractal structure. Consider a finitely ramified fractal lattice such as the Sierpinski gasket or its extensions. A finite order of ramification [8, 9] can be roughly characterized by the following two neccessary conditions: (1) The finite lattice obtained after $n$ steps of the iterative construction of the fractal (called stage- $n$ structure) is connected through only a finite number of “contact sites” with the infinite lattice. (2) For every $n$ the contact sites of a stage- $ö$ -structure can ba mapped bijectively to those of a stage- $(n+1)$ structure. This implies that a random walker on a finitely ramified fractal can leave or enter a stage- $n$ substructure only through a well-defined finite set of boundary (contact) sites (“bottlenecks”).

[p. 399r, §7]
We now decompose the transition matrix ${{}_{n}W}$ of a stage- $n$ structure according to its boundary sites and its interior sites as

${{}_{n}W}=\left[\begin{matrix}{{}_{n}W}_{{11}}&{{}_{n}W}_{{12}}\\ {{}_{n}W}_{{21}}&{{}_{n}W}_{{22}}\end{matrix}\right].$

(6)

An index $1$ corresponds to interior points, $2$ to boundary sites. We then recall from Markov-chain theory that the mean-first-passage time for a random walker starting at the interior site $i$ in the stage- $n$ structure is the $i$ th component of the vector $\langle\mathrm{T}_{n}\rangle$ given by

$\langle\mathrm{T}_{n}\rangle=G1=(I-{{}_{n}W}_{{11}})^{{-1}}1.$

(7)

Here the second equality defines the matrix $G$ , called the Green’s kernel, $I$ is the identity matrix, and $1$ denotes a vector whose components are $1$ .

[p. 399r, §8]
Our goal is to calculate the dynamical critical exponent $z$ for the fractal. The dynamical exponent governs the diffusive behavior on the fractal [10, 11] according to $\langle r^{2}(t)\rangle\propto t^{{2/z}}$ or, equivalently, $\langle T(r)\rangle\propto r^{z}$ in terms of the mean-first-passage time. In the Euclidean case one has $z=2$ . If the fractal dimension for the lattice is $\bar{d}=\log N/\log b$ then $z$ is related to the fracton (spectral) dimension $\tilde{d}$ by $z=2\bar{d}/\tilde{d}$ . Here $b$ is the length scaling factor and $N$ is defined by

$N=\lim _{{n\rightarrow\infty}}\frac{N_{{n+1}}}{N_{n}},$

$N_{n}$ being the number of lattice points in a stage- $n$ structure. To calculate $z$ we wish to utilize our probabilistic Einstein relation, equation (4). For this we consider a random walk starting at a junction of stage- $n$ structures in the fractal lattice. If $m$ stage- $n$ structures meet at $0$ then the number of points in this finite sublattice is roughly $mN_{n}$ . In the long-time limit the stationary probabilities are thus proportional to $1/mN_{n}$ . If the walker makes one step per unit time he spends a fraction of roughly $1/mN_{n}$ of his steps at the origin. Thus we have $\langle T_{{n;00}}\rangle\propto N_{n}$ for the regeneration time on the stage- $n$ structure.

[p. 400l, §0] If we now compare a stage- $n$ with a stage- $(n+1)$ structure we obtain from equation (4)

$\frac{N_{{n+1}}}{N_{n}}=\frac{q_{{n+1}}\langle T_{{n+1}}\rangle}{q_{n}\langle T_{n}\rangle}.$

(8)

Here $\langle T_{n}\rangle$ is the mean-first-passage time to a boundary point and $q_{n}$ is the probability of reaching one of the boundary points without returning to $0$ . Since we have assumed dynamic scaling in the form $\langle T(r)\rangle\propto r^{z}$ it follows that $\kappa\equiv\lim _{{n\rightarrow\infty}}\langle T_{{n+1}}\rangle/\langle T_{n}\rangle$ exists and we can pass to the limit $n\rightarrow\infty$ which yields

$N=h\kappa,$

(9)

where $h\equiv\lim _{{n\rightarrow\infty}}q_{{n+1}}/q_{n}$ . Equation (9) has been called the fractal Einstein relation [5, 12]. It is sometimes written $z=\bar{d}+\zeta$ , where $\zeta$ denotes the length-scaling exponent for the conductivity [1, 13]. This form is obtained from eq. (9) by taking logarithms and dividing by the logarithm of the length scaling factor $b$ .

[p. 400l, §1]
We pause to discuss the significance of these results. First, we remark that for the case of finitely ramified fractals it can be shown [3] that the probabilities $q_{n}$ obey a monotonicity property in the form $0\leq q_{{n+1}}\leq q_{n}\leq 1$ . This leads to the relation $\tilde{d}\leq 2$ , expressing an interessting connection between geometric and dynamic properties. ^b (This is a footnote:) ^bSee [12, p. 33] for a different derivation. Second, eqs. (8) und (9) give rise to a straightforward method of calculating $z$ from numerical similations. One simply measures directly the mean-first-passage times for two scaled structures. Taking their ratios gives $\kappa$ and thus $z$ . While exact calculations are restricted to finitely ramified fractals one can use eqs. (8) und (9) on any network as an approximate method. We expect that this method will converge faster than directly recording $\langle r^{2}(t)\rangle$ and deducing $z$ from $\langle r^{2}(t)\rangle\propto t^{{2/z}}$ . However, care has to be exercised because $\kappa$ is defined as the limit $n\rightarrow\infty$ and it is neccessary to check in any application whether a further increase in the size of the structure will singificantly alter the value of $\kappa$ . Apart from being easily accessible in simulation and numerical calculations [14, 15] mean-first-passage times can be measured directly in photoconductivity experiments on amorphous materials [16], while any experimental determination of $\langle r^{2}(t)\rangle$ has to be indirect.

[p. 400l, §2]
We conclude this paper with two applications. First, we derive the probabilistic analogue of the star-triangle transformation for resistor networks. Second, we calculate the fracton dimension for a fractal tree. Both calculations depend on the method of using mean-first-passage times.

[p. 400l, §3]
Consider the Markov chains for a star and a triangle as specified through the transition matrices,

$W^{\Delta}=\left[\begin{matrix}1-\omega _{1}-\omega _{2}&\omega _{1}&\omega _{2}\\ \omega _{1}&1-\omega _{1}-\omega _{3}&\omega _{3}\\ \omega _{3}&\omega _{2}&1-\omega _{2}-\omega _{3}\end{matrix}\right]$

and

$W^{*}=\left[\begin{matrix}1-\omega^{\prime}_{1}&0&0&\omega^{\prime}_{1}\\ 0&1-\omega^{\prime}_{2}&0&\omega^{\prime}_{2}\\ 0&0&1-\omega^{\prime}_{3}&\omega^{\prime}_{3}\\ \omega^{\prime}_{1}&\omega^{\prime}_{2}&\omega^{\prime}_{3}&1-\omega^{\prime}_{1}-\omega^{\prime}_{2}-\omega^{\prime}_{3}\end{matrix}\right].$

The mean-first-passage times to a site $j$ are obtained by eliminating the $j$ th row and column from $W^{\Delta}$ and $W^{*}$ , respectively, and solving the linear system of equations $(I-\hat{W})\langle T\rangle=1$ , where $\hat{W}$ denotes a reduced transition matrix. We demand that the mean-first-passage times between any two corresponding points $i$ and $j$ ( $i,j=1,2,3$ ) are equal. Solving the resulting systems of linear equations one obtains the star-triangle relations

	$\displaystyle\omega^{\prime}_{1}=\frac{3}{4}\frac{\omega^{{-1}}_{2}\omega^{{-1}}_{3}}{\omega^{{-1}}_{1}+\omega^{{-1}}_{2}+\omega^{{-1}}_{3}},$		(10)
	$\displaystyle\omega^{\prime}_{2}=\frac{3}{4}\frac{\omega^{{-1}}_{1}\omega^{{-1}}_{3}}{\omega^{{-1}}_{1}+\omega^{{-1}}_{2}+\omega^{{-1}}_{3}},$		(11)
	$\displaystyle\omega^{\prime}_{3}=\frac{3}{4}\frac{\omega^{{-1}}_{1}\omega^{{-1}}_{2}}{\omega^{{-1}}_{1}+\omega^{{-1}}_{2}+\omega^{{-1}}_{3}}.$		(12)

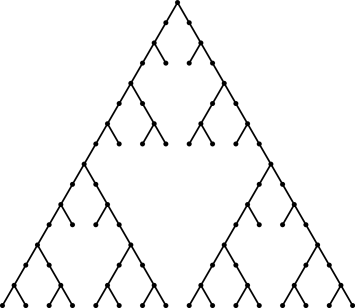
Except for the factor $\tfrac{3}{4}$ this is exactly the star-triangle transformation for resistor networks if one identifies $1/\omega$ with the resistance $R$ . As a final application we determine the fracton dimension of the fractal tree shown in Figure 1. Because of its dangling ends this cannot be calculated exactly via the usual real-space renormalization approach. On the other hand, using the equations for mean-first-passage times, mentioned above, we obtain [3] the exact scaling factor $\kappa=6$ already from stages $n=1,2,3$ . From this the fracton dimension follows ^c (This is a footnote:) ^c[17] have recently obtained the same result. as $\tilde{d}=2(\log 3/\log 6)\approx 1.226\dots$ .

Figure 1: A fractal tree obtained from a Sierpinski gasket.

[p. 400r, §4]
In this paper we have exploited the intimate connections between the mathematical foundations of the Einstein

[p. 401l, §0] relation and the theory of stochastic processes. We have exerted ourselves for a concise derivation of the mathematical result in order to focus on its interpretation and applicability. In a more systematic approach eq. (4) is found to follow from a general relation between generating functions for conditional first-passage probabilities [4]. Here we have established in a probabilistic framework the links between the mathematical approach and the physical picture, both for the ordinary and for the Einstein relation. These results could be used directly in simulation studies and experiments on transport in inhomogeneous media, regardless of whether the systems behave fractally or not.

Authors:	R. Hilfer and A. Blumen
originally published in:	Physical Review A37, No. 2, pages 578-581 (1987)
originally submitted:	June 8th, 1987