II Geometric Characterization of Porous Media

[61.1.4.1] The porosity $\phi$ of a porous medium is defined as the volume of pore space divided by the total volume. [61.1.4.2] The complement of the pore space will be called the matrix. [61.1.4.3] The porosity is the most important geometrical quantity characterizing a porous medium. [61.1.4.4] Clearly, $\phi$ alone, being just a single number, cannot suffice to characterize the complex pore-space geometry. [61.2.0.1] On the other hand, a complete equivalence class of atlantes for the pore-space boundary considered as a two-dimensional continuous manifold contains too much (possibly irrelevant) geometrical information. [61.2.0.2] Similar to many instances in statistical physics, the task is to find a suitable distribution function such that a finite number of its moments give a faithful approximate representation of the system.

[61.2.1.1] It is often suggested to use a “pore-size distribution” as a possible geometric characterization for porous media, and mercury injection is suggested to measure it. [61.2.1.2] Already Scheidegger,[24] however, pointed out that the pore-size distribution is mathematically ill defined. [61.2.1.3] It depends on an arbitrary identification of cylindrical pores and their diameters.[25] [61.2.1.4] It is now well appreciated[26] that the result of a mercury injection measurement cannot be interpreted without having already a faithful geometrical model of the pore space, which itself requires knowledge of the pore-size distribution. [61.2.1.5] Without such a model, no reliable geometrical information such as the pore-size distribution can be extracted from the measurement.

[61.2.2.1] This paper suggests a different characterization of porous media. [61.2.2.2] Purely geometric quantities will be introduced which are well defined and readily accessible to direct measurement. [61.2.2.3] The characterization is based on viewing the local geometry on a mesoscopic scale as the fundamental random quantity. [61.2.2.4] To define “local geometries”, consider a porous medium with a homogeneously and isotropically disordered pore space. [61.2.2.5] The points of a Bravais lattice (in practice a simple cubic lattice) are superimposed on the porous medium and an arbitrary (in parctice cubic) primitive cell is chosen. [61.2.2.6] The local geometry around the lattice point $\mathbf{R}$ is defined as [page 62, §0] the intersection of the pore space and the primitive cell at $\mathbf{R}$ . [62.1.0.1] The volume of the primitive (or measurement) cells is $V_{{{\mathrm{MC}}}}=1/\rho$ , where $\rho$ is the density of Bravais lattice points. [62.1.0.2] This defines the length scale of resolution $L$ as $L=\rho^{{-1/3}}=(V_{{\mathrm{MC}}})^{{1/3}}$ . [62.1.0.3] For the simple cubic lattice with cubic primitive cell, $L$ is the lattice constant. [62.1.0.4] The preceding definition of local geometries is valid for topologically and continuously disordered pore spaces. [62.1.0.5] For a porous medium with substitutional disorder, the measurement lattice is given by the underlying lattice.

[62.1.1.1] The local geometry inside the measurement cell will become increasingly complex as the length scale of resolution $L$ is increased. [62.1.1.2] A full geometric characterization at arbitrary $L$ is difficult. [62.1.1.3] However, at every $L$ the local geometry may be partially characterized by two simple properties. [62.1.1.4] One is the cell porosity; the second is whether the pore space percolates or not.

[62.1.2.1] Consider first the local (or cell) porosity. [62.1.2.2] To define it, the characteristic functions (indicator functions) of an arbitrary set $A$ is introduced as

$\chi _{A}(\mathbf{r})=\begin{cases}0&\text{if}~\mathbf{r}~\text{lies outside the set}~A\\ 1&\text{if}~\mathbf{r}~\text{lies inside the set}~A.\end{cases}$

(2.1)

[62.1.2.3] The local (or cell) porosity $\phi(\mathbf{R},L)$ at the lattice position $\mathbf{R}$ and length scale $L$ is defined as

$\phi(\mathbf{R},L)=\rho\int\chi _{{\mathrm{MC}}}(\mathbf{r};\mathbf{R},L)\chi _{{\mathrm{PC}}}(\mathbf{r})\,\mathrm{d}\mathbf{r},$

(2.2)

where $\chi _{{\mathrm{MC}}}(\mathbf{r};\mathbf{R},L)$ is the characteristic function of the measurement cell at $\mathbf{R}$ having size $L$ , $\chi _{{\mathrm{PC}}}(\mathbf{r})$ is the characteristic function of the pore space and the integration extends over the porous medium. [62.1.2.4] One can now define local porosity distribution functions in analogy to atomic distribution functions. [62.1.2.5] Thus $\mu(\phi,\mathbf{R};L)$ measures the probability density to find the local porosity $\phi$ in the range from $\phi$ to $\phi+\mathrm{d}\phi$ in a cell of linear dimenios $L$ at the point $\mathbf{R}$ . [62.1.2.6] The assumption of homogeneity implies that $\mu(\phi,\mathbf{R};L)=\mu(\phi;L)$ must be independent of $\mathbf{R}$ . [62.1.2.7] The function $\mu(\phi;L)$ will be called the local porosity density at scale $L$ . [62.1.2.8] The bulk porosity $\overline{\phi}$ can be thought of as the integral over a large volume or as the average over a statistical ensemble of measurement cells, and thus, assuming “ergodicity”,

$\overline{\phi}=\phi(\mathbf{R},L\to\infty)=\int _{0}^{1}\phi\mu(\phi;L)\,\mathrm{d}\phi,$

(2.3)

independent of $\mathbf{R}$ and $L$ . [62.1.2.9] Higher-order distribution functions can be defiend similarly. [62.1.2.10] The $n$ -cell local porosity diestribution function $\mu _{n}(\phi _{1},\mathbf{R}_{1};\phi _{2},\mathbf{R}_{2};\dots;\phi _{n},\mathbf{R}_{n};L)$ at scale $L$ measures the probability density to find $\phi _{1}$ in the cell at $\mathbf{R}_{1}$ , $\phi _{2}$ in the cell at $\mathbf{R}_{2}$ etc. [62.1.2.11] The full information about the statistical properties of the porosity distribution at scale $L$ is contained in the local porosity probability functional $\mu(\phi,L)$ at scale $L$ which is obtained as the limit $n\to\infty$ of $\mu _{n}$ .

[62.2.1.1] The local porosity distribution $\mu(\phi;L)$ depends strongly on $L$ . [62.2.1.2] There are two competing effects. [62.2.1.3] At small $L$ the local geometries are simple, but they are highly correlated with each other, and the one-cell function $\mu(\phi;L)$ does not contein these complex geometric correlations. [62.2.1.4] At large $L$ the local geometries are statistically uncorrelated, but each one of them is nearly as complex as the geometry of the full pore space. [62.2.1.5] There must then exist an intermediate length scale $\xi$ at which, on the one hand, the local geometries are relatively simple, and on the other hand the single-cell distribution function has sufficeint nontrivial geometric content to be a good first approximation. [62.2.1.6] In this paper this lenght will be taken as a length of the order of the characteristic pore or grain size of the porous medium. [62.2.1.7] More precisely, $\xi$ is determined from the two-cell distribution function $\mu _{2}(\phi _{1},\mathbf{R}_{1};\phi _{2},\mathbf{R}_{2};L)$ . [62.2.1.8] The assumption of isotropy implies that the two-cell distribution function depends only on the distance $R$ , i.e.

$\mu _{2}(\phi _{1},\mathbf{R}_{1};\phi _{2},\mathbf{R}_{2};L)=\mu _{2}(\phi _{1},\phi _{2};R;L).$

(2.4)

[62.2.1.9] The porosity autocorrelation function at scale $L$ is defined as

$C(R,L)=\frac{\int _{0}^{1}\int _{0}^{1}(\phi _{1}-\overline{\phi})(\phi _{2}-\overline{\phi})\mu _{2}(\phi _{1},\phi _{2};R;L)\mathrm{d}\phi _{1}\mathrm{d}\phi _{2}}{\int _{0}^{1}(\phi-\overline{\phi})^{2}\mu(\phi;R;L)\,\mathrm{d}\phi},$

(2.5)

and the porosity correlation length $\xi$ is obtained from $C(R,L)$ as

$\xi^{2}=\frac{\int R^{2}C(R,0)\,\mathrm{d}^{3}\mathbf{R}}{\int C(R,0)\,\mathrm{d}^{3}\mathbf{R}}.$

(2.6)

[62.0.1.10] In the following the “local porosity distribution” is defined as $\mu(\phi)=\mu(\phi;\xi)$ , the single-cell local porosity density at scale $\xi$ . [62.0.1.11] Simultaneously with this convention it will be assumed that the local geometries at scale $\xi$ are “simple”. [62.0.1.12] This is called the “hypothesis of local simplicity”, and it will be made more precise in Sec. IV. [62.0.1.13] For systems with an underlying lattice symmetry, the length $\xi$ has to be replaced by the lattice constant.

[62.0.2.1] The most important aspect of $\mu(\phi)=\mu(\phi;\xi)$ is that it is readily measureable using modern image-processing equipment. [62.0.2.2] In the following a simplified and approximate procedure to observe $\mu(\phi)$ in homogeneous and isotropic porous media is discussed. [62.0.2.3] This procedure measures $\mu(\phi)$ from photographs of two-dimensional thin sections through the pore space. [62.0.2.4] These photographs must be colored such that pore space and matrix are clearly distinguished. [62.0.2.5] The quality of the pore-space visualization should be such that a high-resolution digitization of the image allows each pixel to be assigned unambigouosly to either pore space or matrix. [62.1.0.1] An approximate correlation length might be calculated by noting that $\lim _{{L\to 0}}\phi(\mathbf{R},L)$ corresponds to the pixel value $0$ or $1$ , according to whether the pixel at position $\mathbf{R}$ falls into matrix $(0)$ or pore space $(1)$ . [62.1.0.2] The porosity autocorrelation function $C(R,0)$ can be calculated from the pixel power spectrum using the Wiener-Khintchine theorem, and the correlation length $\xi$ is obtained from $C(R,0)$ using eq. (2.6). [62.1.0.3] Having determined the correlation length, the photograph is subdivided into cells by placing, e.g., a square grid with squares of length $\xi$ over it. [62.1.0.4] The cell porosities are then

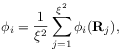$\phi _{i}=\frac{1}{\xi^{2}}\sum _{{j=1}}^{{\xi^{2}}}\phi _{i}(\mathbf{R}_{j}),$

(2.7)

where $\phi _{i}(\mathbf{R}_{j})$ is the pixel at position $\mathbf{R}_{j}$ within cell $i$ . [62.1.0.5] The resulating probability density is averaged over different ways of placing the measurement lattice, over many choices of the primitive cell, and over alle available photographs of two-dimensional sections to obtain the local porosity density $\mu(\phi)$ .

[62.1.1.1] The result of the measuring procedure described in the preceding paragraph will in general lead to a local porosity distribution of the form

$\mu(\phi)=\mu _{0}\delta(\phi)+(1-\mu _{0}-\mu _{1})\widetilde{\mu}(\phi)+\mu _{1}\delta(\phi-1).$

(2.8)

[page 63, §0] [63.1.0.1] Its bulk (average) porosity $\overline{\phi}$ is obtained as the expectation value $\overline{\phi}=\int _{0}^{1}\phi\mu(\phi)\,\mathrm{d}\phi$ , in agreement with eq. (2.3). [63.1.0.2] The local porosity distribution $\mu(\phi)$ contains very much geometrical information about the pore-space geometry. [63.1.0.3] Its definition as $\mu(\phi;\xi)$ is optimal in the sense that it contains the maximum amount of information based purely on the porosity concept. [63.1.0.4] If the cells were chosen much larger than $\xi$ , then the simple form

$\mu(\phi;L\gg\xi)=\delta(\phi-\overline{\phi})$

(2.9)

is expected to result. [63.1.0.5] The geometric information in this case is reduced to $\overline{\phi}$ . [63.1.0.6] At the same time, the local geometries are nearly as complex as the bulk geometry. [63.1.0.7] If, on the other hand, the cells are chosen very small, i.e., $L\ll\xi$ , then the measurement procedure above could still be applied and is expected to yield

$\mu(\phi;L\ll\xi)=\overline{\phi}\delta(\phi-1)+(1-\overline{\phi})\delta(\phi).$

(2.10)

Again, the geometrical information in $\mu(\phi)$ reduced to one number. [63.1.0.8] The geometrical complexity has gone into the correlations between cells contained only in the full porosity probability functional, but not in the single-cell quantity $\mu(\phi)$ . [63.1.0.9] In this sense choosing $L\approx\xi$ is optimal.

[63.1.1.1] The local porosity distribution $\mu(\phi)$ is easily calculated for ordered or substitutionally disordered porous media, but very dificult to obtain for topological or continuum disorder. [63.1.1.2] For ordered or substitutionally disordered cases, the measurement is given by the underlying lattice, and $\xi$ is the lattice constant. [63.1.1.3] One finds immediately $\mu(\phi)=\delta(\phi-\overline{\phi})$ for the ordered case, in agreement with eq. (2.9). [63.1.1.4] For substitutional disorder the local porosity density follows directly from the distribution of the individual geometrical elements which occupy the lattice sites.

[63.1.2.1] The second geometric propery to characterize local geometries is whether the pore space percolates or not. [63.1.2.2] For cubic cells each cell is classified as percolating or nonpercolating according to whether or not there exists at least one face of the cube which can be connected to any of the other faces via a path contained completely inside the pore space. [63.1.2.3] For noncubic cells the classification has to be modified appropriately. [63.1.2.4] Let $\lambda(\phi)$ denote the fraction of percolating cells with local porosity $\phi$ . [63.1.2.5] $\lambda(\phi)$ will be called the “local percolation probability”. [63.1.2.6] It is an important geometric quantity for all physical properties of porous media such as conduction or fluid flow because it determines whether volume elements are permeable or not.

[63.1.3.1] Twe two function $\mu(\phi)$ and $\lambda(\phi)$ constitute only a partial and approximate geometric characterization of the pore space. [63.1.3.2] However, $\lambda$ and $\mu$ have a rich geometrical content. [63.1.3.3] This becomes obvious from the difficulty of calculating them even for the simplest models of homogeneous and isotropic porous media. [63.1.3.4] At present, no experimentally observed local porosity distributions or percolation probabilities are available to the author.[27] [63.1.3.5] However, I believe that the general shape of $\mu(\phi)$ for pore spaces resulting from spinodal decomposition may be similar to the order-parameter distribution of a two-dimensional Lennard-Jones fluid measured in a recent computer experiment.[28]

Author:	R. Hilfer
published in:	Physical Review Letters: B, Vol. 44, No. 1, pages 60-75 (July, 1991)
originally submitted:	12th October 1990