III Statistical Mechanics

A Ensemble Limit

[p. 2469l, §2]
Given the thermodynamic classification of phase transitions it is natural to ask whether anequilibrium phase transitions and a statistical-mechanical classification corresponding to the thermodynamic scheme exist for critical behavior in statistical mechanics. These questions are discussed in the following sections. Statistical mechanics for noncritical systems is based on the law of large numbers [30]. This suggests that the theory of critical phenomena may be founded in the theory of stable laws. Although natural this idea is usually rejected because the divergence of correlation lengths and susceptibilities appears to imply that the microscopic random variables are strongly dependent [31, 32, 33] while the standard theory of stable laws applies only to weakly dependent or independent variables [28, 34, 35].

[p. 2469l, §3]
The problem of strong dependence arises from the particular choice of performing the infinite-volume limit and the continuum limit. One usually starts from an infinite-volume lattice theory and then asks for possible continuum (or scaling) limits of the rescaled infinite-volume correlation functions [33]. Depending on whether the rescaled correlation lengths remain finite or not one distinguishes the “massive” and the “massless” scaling limit but in either case the infinite-volume limit has been performed before taking the scaling limit.

[p. 2469l, §4]
The idea of the present paper for basing a statistical classification of critical behavior on the theory of stable laws is related to that of finite-size scaling [36, 37, 38, 39, 40] and

[p. 2469r, §4]
uses a different method of taking infinite-volume and continuum limits. Consider a $d$ -dimensional simple cubic lattice with lattice spacing $a>0$ in âblock geometryâ, i. e., having finite side length $L<\infty$ in all $d$ directions. Let $X$ be a scalar observable associated with each lattice point. The lattice represents a discretization of a large but finite statistical-mechanical system [41]. Let the lengths $a,L$ and the parameters $H$ of the statistical-mechanical system be such that

$0<a\ll\xi _{X}(\Pi)\ll L<\infty\,.$

(3.1)

Thus the system decomposes into a large number of uncorrelated blocks of linear extension $\xi _{X}$ . The ensemble limit is defined as the simultaneous limit in which

$a\rightarrow 0\,,\ L\rightarrow\infty\,,\ \Pi\rightarrow\Pi _{c}\ \ \ \ \text{such that}\ \ \ \ \xi _{X}(\Pi)\rightarrow\xi _{X}(\Pi _{c})<\infty\,.$

(3.2a)

Two cases can be distinguished: In the critical ensemble limit

$0<\xi _{X}(\Pi _{c})<\infty\,,$

(3.2b)

while for the noncritical ensemble limit

$\xi _{X}(\Pi _{c})=0\,.$

(3.2b)

[p. 2469r, §5]
If $N=(L/\xi _{X})^{d}$ denotes the number of uncorrelated blocks of size $\xi _{X}$ and $M=(\xi _{X}/a)^{d}$ is the number of sites in each block then $NM=(L/a)^{d}$ is the total number of lattice sites. The correlation length $\xi _{X}$ diverges in units of $a$ in the critical ensemble limit but stays finite in the noncritical ensemble limit. Note also that $N\rightarrow\infty$ in the critical ensemble limit while $N$ remains finite in the massive scaling limit or the finite-size scaling limit [37]. The critical ensemble limit generates an infinite ensemble of uncorrelated blocks. This feature allows the application of standard limit theorems for uncorrelated or weakly dependent variables.

[p. 2469r, §6]
Let $X_{{iN}}(j)$ denote the scalar observable $X$ at lattice site $j~(j=1,...,M)$ inside block $i~(i=1,...,N)$ . Then

$X_{{iN}}=\sum^{M}_{{j=1}}X_{{iN}}(j)$

(3.3a)

are the block sums or block variables for block $i$ and

$X_{N}=\sum^{N}_{{i=1}}X_{{iN}}$

(3.3b)

is the ensemble sum or ensemble variable for the total system. The $X_{{iN}}(j)$ are random variables and so are $X_{{iN}}$ and $X_{N}$ . Let

$\tilde{X}_{N}=(X_{N}-C_{N})/D_{N}$

(3.4)

denote the normed and centered ensemble sum and let $P_{N}(x)={\mathrm{Prob}}\{ X_{N}<x\}$ be the probability distribution function of $X_{N}$ . Assuming translation invariance the block variables are uncorrelated and identically distributed. Therefore the limiting distribution of $\tilde{X}_{N}$ is stable in the critical ensemble limit [28, 34, 35]. More precisely, if

$P(x)=\lim _{{N\rightarrow\infty}}P_{N}(xD_{N}+C_{N})$

(3.5)

[p. 2470l, §0]
denotes the limiting distribution function of the normed ensemble sums (3.4) then the characteristic function $p(k)=\int^{\infty}_{{-\infty}}\exp(ikx)dP(x)$ of $P(x)$ has the representation

$\log p(k)=iCk-D\lvert k\rvert^{{{\tilde{\omega}}}}\left(1-i\zeta\frac{k}{\lvert k\rvert}\omega(k,{\tilde{\omega}})\right),$

(3.6)

where ${\tilde{\omega}},\zeta,C,D$ are constants whose ranges are

$\displaystyle 0<{\tilde{\omega}}$	$\displaystyle\leq 2,$	(3.7a)
$\displaystyle-1\leq\zeta$	$\displaystyle\leq 1,$	(3.7b)
$\displaystyle-\infty<C$	$\displaystyle<\infty,$	(3.7c)
$\displaystyle D$	$\displaystyle\geq 0,$	(3.7d)

and

$\omega(k,{\tilde{\omega}})=\begin{cases}\tan\left(\frac{{\tilde{\omega}}\pi}{2}\right),&\text{for }{\tilde{\omega}}\neq 1,\\ \frac{2}{\pi}\log\lvert k\rvert,&\text{for }{\tilde{\omega}}=1.\end{cases}$

(3.8)

The constant ${\tilde{\omega}}$ is called the index of the stable distribution while the parameter $\zeta$ characterizes its symmetry or skewness.

[p. 2470l, §1]
If the limit in (3.5) exists and $D>0$ then the norming constants $D_{N}$ must have the form [28, 35]

$D_{N}=N^{{1/{\tilde{\omega}}}}\Lambda(N),$

(3.9)

where the function $\Lambda(N)$ is slowly varying at infinity. The case $D>0$ corresponds to the critical ensemble limit, while for $Q=0$ the limiting distribution $P(x)$ is degenerate, i. e., concentrated at a single point, corresponding to the noncritical ensemble limit.

[p. 2470l, §2]
The preceding limit theorem implies that in the limit $N\rightarrow\infty$ the distribution function of the block sums can be approximated as

$P_{N}(x)\approx P\left(\frac{x-C_{N}}{D_{N}};{\tilde{\omega}},\zeta,C,D\right),$

(3.10)

where the notation $P(x;{\tilde{\omega}},\zeta,C,D)$ is introduced for stable distributions of index ${\tilde{\omega}}$ . The objective in the next section will be to establish a large- $N$ scaling result for $P_{N}(x)$ . To obtain it more information on the common distribution of the individual block variables is required.

[p. 2470l, §3]
The limiting distributions $\tilde{P}(x)$ of the individual block variables $X_{{iN}}$ are independent of $i$ because of translation invariance and they belong to the domain of attraction of a stable law. The class of possible block variable limits can thus be characterized as follows [35]: In order that the characteristic function $\tilde{p}(k)$ of $\tilde{P}(x)$ belongs to the domain of attraction of a stable law whose characteristic function has the logarithm $-D\lvert k\rvert^{{{\tilde{\omega}}}}[1-i\zeta(k/\lvert k\rvert)\omega(k,{\tilde{\omega}})]$ with ${\tilde{\omega}}$ , $\zeta$ , $D$ and $\omega(k,{\tilde{\omega}})$ as in (3.8)-(3.10), it is necessary and sufficient that in the neighborhood of the origin $k=0$

$\log\tilde{p}(k)=i\tilde{C}k-D\lvert k\rvert^{{\tilde{\omega}}}\tilde{\Lambda}(k)\left(1-i\zeta\frac{k}{\lvert k\rvert}\omega(k,{\tilde{\omega}})\right),$

(3.11)

[p. 2470r, §3]
where $\tilde{C}$ is a constant and $\tilde{\Lambda}(k)$ is a slowly varying function for $k\rightarrow 0$ .

[p. 2470r, §4]
Equations (3.9) or (3.11) show that each ensemble limit $N,M\rightarrow\infty$ is labeled by a set of numbers ${\tilde{\omega}}$ , $\zeta$ , $D$ with ranges as in (3.7) and a slowly varying function $\Lambda$ . While $D$ differentiates between critical and noncritical limits ${\tilde{\omega}}$ , $\zeta$ , and $\Lambda$ differentiate between different critical ensemble limits. This characterization is reminiscent of the thermodynamic classification scheme and suggests a closer correspondence. To establish such a correspondence it is necessary to relate the generalized orders $\lambda$ in the thermodynamical classification scheme to the numbers ${\tilde{\omega}},\zeta$ occurring in the characterization of ensemble limits. This will be done in the next section.

B Finite-ensemble scaling

[p. 2470r, §5]
The purpose of the present section is to investigate the $N$ dependence of the probability distribution for ensemble sums $X_{N}$ in the limit of large $N$ . The scaling relations emerging from this analysis will be called finite-ensemble scaling because they are closely related to finite-size-scaling relations by virtue of the similarity between the critical ensemble limit defined above and the finite-size-scaling limit [37]. The question is how to choose the norming and centering constants $C_{N}$ , $D_{N}$ in (3.10) given the characterization (3.11) for the individual block variables $X_{{iN}}$ .

The centering constants $C_{N}$ in Eq. (3.10) can be eliminated from the problem by setting $C_{N}=-C^{\prime}D_{N}$ where

$C^{\prime}=\begin{cases}C,&\text{for }{\tilde{\omega}}\neq 1,\\ C+\frac{2}{\pi}\zeta D\log D,&\text{for }{\tilde{\omega}}=1,\end{cases}$

(3.12)

and with this choice (3.10) becomes

$P_{N}(x)\approx P\left(\frac{x-C_{N}}{D_{N}};{\tilde{\omega}},\zeta,C,D\right)=P\left(\frac{x}{D^{{1/{\tilde{\omega}}}}D_{N}};{\tilde{\omega}},\zeta,0,1\right).$

(3.13)

Although the general form of $D_{N}$ is known from (3.9) it remains to establish the relationship between the slowly varying functions in (3.9) and (3.11). Once this relation is established Eq. (3.12) represents a finite $N$ scaling formula for a system in which the individual block variable limits are characterized by (3.11).

[p. 2470r, §6]
The limiting distribution functions of the individual block variables $X_{{iN}}$ have characteristic functions as given by (3.11). Introduce

$R(k)=\lvert k\rvert^{{\tilde{\omega}}}\mathfrak{L}(k^{{\tilde{\omega}}})$

(3.14)

where the slowly varying function $\mathfrak{L}(x)$ is defined through

$\tilde{\Lambda}(k)=\mathfrak{L}(k^{{\tilde{\omega}}})$

(3.15)

and $\tilde{\Lambda}(k)$ is the slowly varying function appearing in (3.11). For sufficiently large $N$ the norming constants $D_{N}$

[p. 2471l, §0]
are chosen as

$D_{N}^{{-1}}=\inf\left\{ k>0:R(k)=\frac{D}{N}\right\}$

(3.16)

[p. 2471r, §0]
which is possible because $R(k)\rightarrow 0$ for $k\rightarrow 0$ and $R(k)$ is continuous in a neighborhood of zero. Then for small $k$ [35]

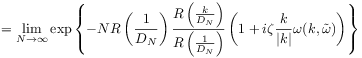$\displaystyle\lim _{{N\rightarrow\infty}}\left\{\tilde{p}\left(\frac{k}{D_{N}}\right)\right\}^{N}$	$\displaystyle=\lim _{{N\rightarrow\infty}}\exp\left\{-NR\left(\frac{1}{D_{N}}\right)\frac{R\left(\frac{k}{D_{N}}\right)}{R\left(\frac{1}{D_{N}}\right)}\left(1+i\zeta\frac{k}{\lvert k\rvert}\omega(k,{\tilde{\omega}})\right)\right\}$
	$\displaystyle=\exp\left\{-D\lvert k\rvert^{{\tilde{\omega}}}\left(1+i\zeta\frac{k}{\lvert k\rvert}\omega(k,{\tilde{\omega}})\right)\right\}.$		(3.17)

[p. 2471l, §0]
It follows that $D\approx NR(1/D_{N})$ for sufficiently large $N$ and this determines $D_{N}$ in terms of $\tilde{\Lambda}(k)$ and ${\tilde{\omega}}$ as

$D_{N}=\left(\frac{N}{D\mathfrak{L}^{*}(N^{{-1}})}\right)^{{1/{\tilde{\omega}}}},$

(3.18)

where $\mathfrak{L}^{*}(x)$ is the conjugate slowly varying function to $\mathfrak{L}(x)$ defined in Eq. (3.18). The slowly varying function $\Lambda(N)$ appearing in (3.9) is thus given as

$\Lambda(N)=\left(D\mathfrak{L}^{*}\left(\frac{1}{N}\right)\right)^{{-1/{\tilde{\omega}}}}.$

(3.19)

in terms of $\tilde{\Lambda}(k)$ appearing in the limiting distributions (3.11) for the individual blocks.

[p. 2471l, §1]
Finally Eq. (3.12) gives the finite-ensemble scaling for the distribution of ensemble variables $X_{N}$ in the large- $N$ limit

$P_{N}(x)=P\left(\frac{x\mathfrak{L}^{{*1/{\tilde{\omega}}}}(N^{{-1}})}{N^{{1/{\tilde{\omega}}}}};{\tilde{\omega}},\zeta,0,1\right).$

(3.20)

More interesting than the ensemble variables $X_{N}$ are the ensemble averages defined as $\bar{X}_{N}=X_{N}/(NM)$ . The probability distribution function $\bar{P}_{N}(\bar{x})$ for the ensemble averages $X_{N}$ has the finite-ensemble-scaling form

$\bar{P}_{N}(\bar{x})=\bar{P}\left(\frac{\bar{x}\mathfrak{L}^{{*1/{\tilde{\omega}}}}(N^{{-1}})}{N^{{(1-{\tilde{\omega}})/{\tilde{\omega}}}}};{\tilde{\omega}},\zeta,0,1\right).$

(3.21)

If $N=(L/\xi _{X})^{d}$ is expressed in terms of the system size $L$ they are seen to be closely related to finite-size-scaling theory. Note that Eqs. (3.20) and (3.21) are derived without reference to a particular model or approximate critical Hamiltonian such as the Landau-Ginzburg-Wilson Hamiltonian. They are generally valid for all translationâinvariant critical systems, i. e., systems for which the basic limit distribution (3.5) is not degenerate.

C Identification of exponents and statistical classification scheme

[p. 2471l, §2]
It is now possible to consider the correspondence between the statistical classification in terms of ${\tilde{\omega}}$ , $\zeta$ , and $\tilde{\Lambda}$ and the thermodynamic classification in terms of $\lambda$ and $\Lambda$ .

[p. 2471r, §2]
To do this the index ${\tilde{\omega}}$ in (3.20) and (3.21) must be related to the critical exponents. This is immediately possible from (3.21) by considering for example the order parameter $\Psi$ . Setting $X=\Psi$ , taking the derivative with respect to $\bar{x}$ in Eq. (3.21) and using $N=(L/\xi _{\Psi})^{d}$ one finds that the $k$ th moment $\langle\bar{\Psi}^{k}\rangle$ of the order parameter scales with system size as $\langle\bar{\Psi}^{k}\rangle\sim L^{{kd({\tilde{\omega}}-1)/{\tilde{\omega}}}}$ . Comparing to standard finite-size-scaling theory [36, 37, 38, 39, 40] relates ${\tilde{\omega}}$ to the thermodynamic exponents as

${\tilde{\omega}}_{\Psi}=\frac{\gamma+2\beta}{\gamma+\beta}=1+\frac{1}{\delta}=\lambda _{\Psi},$

(3.22)

where $\beta$ and $\gamma$ are the order parameter and susceptibility exponents, and $\lambda _{\Psi}$ , was defined in (2.5). Similarly for the energy density $X=\mathscr E$ one finds

${\tilde{\omega}}E=2-\alpha=\lambda E$

(3.23)

where $\lambda E$ is the thermal order of (2.5). This suggests that the correspondence between the statistical and the thermodynamic classification of phase transitions is given generally as ${\tilde{\omega}}=\lambda$ . Note that second-order (i. e., self-conjugate) phase transition occupy again a special place in the statistical classification scheme because of the bound ${\tilde{\omega}}\leq 2$ in (3.7a). This fact will be related below to violations of hyperscaling relations.

[p. 2471r, §3]
Anequilibrium phase transitions with order $\lambda<1$ correspond to stable limit distributions with index ${\tilde{\omega}}<1$ . Thus anequilibrium transitions are not only predicted by equilibrium thermodynamics but also by equilibrium statistical mechanics. The fact that anequilibrium transitions restrict the range of equilibrium temperatures as in (2.17) is mirrored by the fact that expectation values of averages diverge in the critical ensemble limit for anequilibrium critical points with ${\tilde{\omega}}<1$ . This implies that the traditional formulation of statistical mechanics becomes inapplicable at anequilibrium critical points just as traditional thermodynamics becomes inapplicable.

[p. 2471r, §4]
While the general correspondence between $\lambda<1$ and ${\tilde{\omega}}<1$ is reassuring it is not sufficient to establish the existence of anequilibrium phase transitions in statistical mechanics. To demonstrate their existence requires a possibly exact calculation of the partition sum for a concrete statistical-mechanical model. It is possible to demonstrate the existence of anequilibrium transitions in

[p. 2472l, §0]
this way. A concrete example occurs in what is perhaps the simplest model in the theory of critical phenomena, namely, the one-dimensional Gaussian model [42]. This finding is important because the Gaussian model is of central importance in the modern theory of critical phenomena as the starting point for systematic perturbative calculations [6]. The model Hamiltonian is $\mathscr H=-(J/2)\sum\Psi _{i}\Psi _{j}$ where the sum runs over all nearest-neighbour pairs of lattice sites $i$ , $j$ and the continuous spin variables $\Psi _{i}$ have a Gaussian single spin measure proportional to $\exp[-\sigma\Psi^{2}_{i}]$ . The limiting free-energy density for the one-dimensional Gaussian model is well known and it reads

$-\frac{f(T)}{k_{B}T}=\frac{1}{2}\log\pi-\frac{1}{2}\log\left(\tfrac{1}{2}[\sigma+(\sigma^{2}-K^{2})^{{1/2}}]\right),$

(3.24)

where $K=J/(k_{B}T)$ and $k_{B}$ denotes Boltzmannâs constant. The exact free-energy density (3.24) for the one-dimensional Gaussian model exhibits an anequilibrium transition of order $\lambda E=\frac{1}{2}$ at the critical temperature $T_{{\mathrm{min}}}=J/(k_{B}\sigma)$ .

D General mechanism for the violation of hyperscaling

[p. 2472l, §1]
The identification $\lambda={\tilde{\omega}}$ cannot hold for all values of $\lambda>0$ because ${\tilde{\omega}}\leq 2$ is required by (3.7). The new restriction ${\tilde{\omega}}\leq 2$ is now seen to be related to the violation of hyperscaling and the breakdown of finite-size scaling for thermal fluctuations in dimensions $d>4$ . Consider the class of statistical-mechanical models obeying the Lebowitz inequality for the four-point functions and infrared bounds for the two-point functions [33]. For such models the susceptibility exponent $\gamma$ obeys $\gamma\leq 1$ and the correlation-function exponent $\eta$ obeys $\eta\geq 0$ . Then using ${\tilde{\omega}}\leq 2$ , the Fisher inequality $\gamma\leq(2-\eta)\nu$ , the hyperscaling relation $d\nu=2-\alpha$ , and relation (3.23) the following chain of inequalities is obtained:

$d\leq d\gamma\leq(2-\eta)d\nu=(2-\eta)(2-\alpha)=(2-\eta){\tilde{\omega}}E\leq 2(2-\eta)\leq 4.$

(3.25)

For general models hyperscaling may fail at ${\tilde{\omega}}=2$ because there are distributions with nonalgebraic tails within the domain of attraction of the normal law. Note that in this way the inequality ${\tilde{\omega}}\leq 2$ provides a general mechanism for the breakdown of hyperscaling independent of identifying dangerous irrelevant variables in a particular model. Analogous breakdown phenomena are expected to occur for critical fluctuations in observables other than the energy density.

Authors:	R. Hilfer
originally published in:	Physical Review E48, No. 2, pages 2466-2475 (1993)
originally submitted:	January 29th, 1993