Sie sind hier: ICP » R. Hilfer » Publikationen

II Critical finite-size scaling functions

[69.1.1.1] We consider the two-dimensional Ising model on a square lattice of side length L. The N=L^{2} spins \sigma _{i}=\pm 1 interact according to the Hamiltonian \mathcal{H}=-J\sum _{{(i,j)}}\sigma _{i}\sigma _{j}-H\sum _{{i=1}}^{N}\sigma _{i} where J>0 is the ferromagnetic coupling strength and H is an external field. [69.1.1.2] The first summation \sum _{{(i,j)}} runs over all nearest neighbour pairs on the lattice. [69.1.1.3] The order parameter is the magnetization per spin

m=\frac{1}{N}\sum _{{i=1}}^{{N}}\sigma _{i} (1)

whose value fulfills -1\leq m\leq 1. [69.1.1.4] In the following we set J=1 and also the Boltzmann constant to unity. [69.1.1.5] We denote the temperature by T, and write h=H/(k_{B}T) for the magnetic field.

In this paper we focus on the probability density p(m) of the order parameter defined as

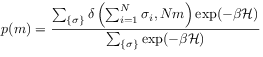p(m)=\frac{\sum _{{\{\sigma\}}}\delta\left(\sum _{{i=1}}^{{N}}\sigma _{i},Nm\right)\exp(-\beta\mathcal{H})}{\sum _{{\{\sigma\}}}\exp(-\beta\mathcal{H})} (2)

where \beta=1/(k_{B}T), \delta(i,j)=\delta _{{ij}} is a Kronecker \delta, and where m is such that |Nm/2| is an integer not larger than N/2. [69.1.1.6] The probability density p(m) depends parametrically on temperature T, field h and system size N=L^{2},

p(m)=p(m;T,h,L). (3)

It is also called order parameter distribution. [69.1.1.7] In the following we limit ourselves to the case h=0, and hence p(m)=p(m;T,L). [69.1.1.8] The critical order parameter distribution is obtained in the limit L\to\infty and T\to T_{c} where T_{c}=2/{\rm arsinh}(1)\approx 2.2691853... is the critical temperature. [69.1.1.9] There are different ways of taking this limit (see [23] for an overview). [69.1.1.10] Traditionally this limit is understood as the finite-size scaling limit defined by

L\to\infty,\ T\to T_{c}\ \ \quad\text{such that}\ \ \quad L/\xi\approx 1<\infty (4)

where \xi=\xi(T) is the temperature dependent spin-spin-correlation length for the infinite system. [69.1.1.11] Note that in an infinite system \xi(T)\to\infty as T\to T_{c}. [69.1.1.12] A second way to take the limit is the finite ensemble scaling limit defined through [23]

L\to\infty,\ T\to T_{c}\ \ \quad\text{ such that }\ \ \quad L/\xi\to\infty. (5)

[69.2.0.1] All other possibilities for taking the limits are discussed in [23]. [69.2.0.2] It is often postulated that \xi fulfills the finite size scaling hypothesis

\xi(t,L)=L\widetilde{\xi}(tL^{{1/\nu}}) (6)

in the finite-size scaling limit. [69.2.0.3] Here t=(T-T_{c})/T_{c} is the reduced temperature, \widetilde{\xi}(x) is a universal scaling function and \nu is the correlation length exponent. For the two-dimensional Ising model \nu=1.

[69.2.1.1] The traditional finite-size scaling hypothesis [13, 24] for the critical order parameter distribution assumes that

p(m;T=T_{c},L)=p(m;L)=L^{{\beta/\nu}}\widetilde{p}(mL^{{\beta/\nu}}) (7)

where \widetilde{p}(x) is the universal scaling function of the order parameter distribution and \beta is the order parameter exponent. [69.2.1.2] For the two-dimensional Ising model [25]

\beta=\frac{1}{8}. (8)

Our scaling variable is then

x=mL^{{1/8}}. (9)

Using the scaling assumption (7) one obtains the absolute moments of the critical order parameter distribution

\langle|m|^{k}\rangle(L)=\int|m|^{k}p(m;L){\rm d}m=L^{{-k\beta/\nu}}\widetilde{m}_{k} (10)

where

\widetilde{m}_{k}=\int|x|^{k}\widetilde{p}(x){\rm d}x. (11)

[69.2.1.3] From these one calculates the so called renormalized coupling constant g=\widetilde{m}_{4}/\widetilde{m}_{2}^{2} or the Binder cumulant

U_{L}=1-\frac{\widetilde{m}_{4}}{3\widetilde{m}_{2}^{2}} (12)

which are often used in studies of critical behaviour because they are independent of L at criticality, if all the assumptions are valid.