| 1 |
Adler, P. (1992).
Porous Media.
Butterworth-Heinemann, Boston.
|
| 2 |
Bakke, S. and Øren, P. (1997).
3-d pore-scale modeling of sandstones and flow simulations in pore
networks.
SPE Journal, 2:136.
|
| 3 |
Barut, A. and Raczka, R. (1986).
Theory of Group Representations and Applications.
World Scientific, Singapore.
|
| 4 |
Bear, J. (1972).
Dynamics of Fluids in Porous Media.
Elsevier Publ. Co., New York.
|
| 5 | Bear, J. and Verruijt, A. (1987).
Modeling Groundwater Flow and Pollution.
Kluwer Academic Publishers, Dordrecht.
|
| 6 |
Biswal, B., Manwart, C., and Hilfer, R. (1998).
Threedimensional local porosity analysis of porous media.
Physica A, 255:221.
|
| 7 |
Biswal, B., Manwart, C., Hilfer, R., Bakke, S., and Øren, P. (1999).
Quantitative analysis of experimental and synthetic microstructures
for sedimentary rock.
Physica A, 273:452.
|
| 8 |
Bryant, S., Mellor, D., and Cade, C. (1993).
Physically representative network models of transport in porous
media.
AIChE Journal, 39:387.
|
| 9 |
Chatzis, I. and Dullien, F. (1977).
Modelling pore structure by 2-d and 3-d networks with applications to
sandstones.
J. of Canadian Petroleum Technology, page 97.
|
| 10 |
Crivelli-Visconti(ed.), I. (1998).
ECCM-8 European Conference on Composite Materials.
Woodhead Publishing Ltd, Cambridge.
|
| 11 |
Delfiner, P. (1972).
A generalization of the concept of size.
J. Microscopy, 95:203.
|
| 12 |
Diebels, S. and Ehlers, W. (1996).
On fundamental concepts of multiphase micropolar materials.
Technische Mechanik, 16:77.
|
| 13 |
Dullien, F. (1992).
Porous Media - Fluid Transport and Pore Structure.
Academic Press, San Diego.
|
| 14 |
Ehlers, W. (1995).
Grundlegende Konzepte in der Theorie poröser Medien.
Technical report, Institut f. Mechanik, Universität Stuttgart,
Germany.
|
| 15 |
Fatt, I. (1956).
The network model of porous media I. capillary pressure
characteristics.
AIME Petroleum Transactions, 207:144.
|
| 16 |
Hadwiger, H. (1955).
Altes und Neues über konvexe Körper.
Birkhäuser, Basel.
|
| 17 |
Haslund, E., Hansen, B., Hilfer, R., and Nøst, B. (1994).
Measurement of local porosities and dielectric dispersion for a water
saturated porous medium.
J. Appl. Phys., 76:5473.
|
| 18 |
Hearst, J. and Nelson, P. (1985).
Well Logging for Physical Properties.
McGraw-Hill, New York.
|
| 19 |
Hilfer, R. (1991).
Geometric and dielectric characterization of porous media.
Phys. Rev. B, 44:60.
|
| 20 |
Hilfer, R. (1992).
Local porosity theory for flow in porous media.
Phys. Rev. B, 45:7115.
|
| 21 |
Hilfer, R. (1993).
Local porosity theory for electrical and hydrodynamical transport
through porous media.
Physica A, 194:406.
|
| 22 |
Hilfer, R. (1996).
Transport and relaxation phenomena in porous media.
Advances in Chemical Physics, XCII:299.
|
| 23 |
Hilfer, R., B.Nøst, E.Haslund, Th.Kautzsch, B.Virgin, and B.D.Hansen (1994).
Local porosity theory for the frequency dependent dielectric function
of porous rocks and polymer blends.
Physica A, 207:19.
|
| 24 |
Hilfer, R., Rage, T., and Virgin, B. (1997).
Local percolation probabilities for a natural sandstone.
Physica A, 241:105.
|
| 25 |
Katz, A. and Thompson, A. (1986).
Quantitative prediction of permeability in porous rock.
Phys. Rev. B, 34:8179.
|
| 26 |
Lake, L. (1989).
Enhanced Oil Recovery.
Prentice Hall, Englewood Cliffs.
|
| 27 |
Levitz, P. and Tchoubar, D. (1992).
Disordered porous solids: From chord distributions to small angle
scattering.
J. Phys. I France, 2:771.
|
| 28 |
Manwart, C. and Hilfer, R. (1999).
to be published.
|
| 29 |
Manwart, C., Torquato, S., and Hilfer, R. (2000).
Stochastic reconstruction of sandstones.
Phys.Rev.E, 62:893.
|
| 30 |
Marsily, G. (1986).
Quantitative Hydrogeology – Groundwater Hydrology for
Engineers.
Academic Press, San Diego.
|
| 31 |
Mecke, K. and Wagner, H. (1991).
Euler characteristic and related measures for random geometric sets.
J. Stat. Phys., 64:843.
|
| 32 |
Muche, L. and Stoyan, D. (1992).
Contact and chord length distributions of the poisson voronoi
tessellation.
Journal of applied probability, 29:467.
|
| 33 | Quiblier, J. (1984).
A new three dimensional modeling technique for studying porous media.
J. Colloid Interface Sci., 98:84.
|
| 34 |
Roberts, A. (1997).
Statistical reconstruction of three-dimensional porous media from
two-dimensional images.
Phys.Rev.E, 56:3203.
|
| 35 |
Roberts, J. and Schwartz, L. (1985).
Grain consolidation and electrical conductivity in porous media.
Phys. Rev. B, 31:5990.
|
| 36 |
Roy, S. and Tarafdar, S. (1997).
Archies’s law from a fractal model for porous rock.
Phys.Rev.B, 55:8038.
|
| 37 |
Sahimi, M. (1993).
Flow phenomena in rocks: From continuum models to fractals,
percolation, cellular automata and simulated annealing.
Rev. Mod. Phys., 65:1393.
|
| 38 |
Sahimi, M. (1995).
Flow and Transport in Porous Media and Fractured Rock.
VCH Verlagsgesellschaft mbH, Weinheim.
|
| 39 |
Scheidegger, A. (1974).
The Physics of Flow Through Porous Media.
University of Toronto Press, Toronto.
|
| 40 |
Schneider, R. (1993).
Convex Bodies: The Brunn-Minkowski Theory.
Cambridge University Press, Cambridge.
|
| 41 |
Schneider, R. and Weil, W. (1992).
Integralgeometrie.
Teubner, Stuttgart.
|
| 42 |
Stell, G. (1985).
Mayer-Montroll equations (and some variants) through history for
fun and profit.
In Shlesinger, M. and Weiss, G., editors, The Wonderful World of
Stochastics, page 127, Amsterdam. Elsevier.
|
| 43 |
Stoyan, D., Kendall, W., and Mecke, J. (1995).
Stochastic Geometry and its Applications.
Akademie-Verlag / Wiley, Berlin / Chichester.
|
| 44 |
Torquato, S. and Stell, G. (1982).
Microstructure of Two Phase Random Media I: The 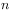 -Point
Probability Functions.
J. Chem. Phys., 77:2071. -Point
Probability Functions.
J. Chem. Phys., 77:2071.
|
| 45 |
Virgin, B., Haslund, E., and Hilfer, R. (1996).
Rescaling relations between two- and three dimensional local porosity
distributions for natural and artificial porous media.
Physica A, 232:1.
|
| 46 |
Widjajakusuma, J., Biswal, B., and Hilfer, R. (1999a).
Quantitative prediction of effective material properties of
heterogeneous media.
Comp. Mat. Sci., 16:70.
|
| 47 |
Widjajakusuma, J., Manwart, C., Biswal, B., and Hilfer, R. (1999b).
Exact and approximate calculations for conductivity of sandstones.
Physica A, 270:325.
|
| 48 |
Yeong, C. and Torquato, S. (1998).
Reconstructing random media.
Phys.Rev. E, 57:495.
|
| 49 |
Ziman, J. (1982).
Models of Disorder.
Cambridge University Press, Cambridge.
|
