3 Initial Conditions, Boundary Conditions and Model Parameters
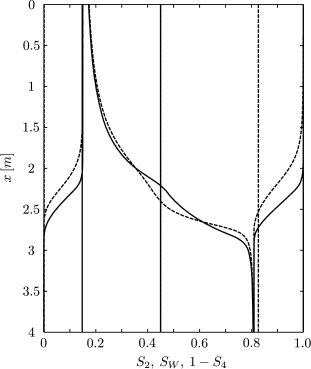
[513.4.1] Consider a cylindrical column containing a homogeneous, isotropic and incompressible porous medium. [513.4.2] The column is closed at both ends and filled with two immiscible fluids. [513.4.3] Assume that the surface and interfacial tensions are such that the capillary fringe is much thicker than the column diameter so that a onedimensional description is appropriate.
[513.5.1] The experimental situation considered here is
that of raising a closed column as described in [26, p. 223].
[513.5.2] It is illustrated in Figure 1.
[513.5.3] Initially, at instant ![]() , both fluids are at rest.
[513.5.4] The column is oriented horizontally (
, both fluids are at rest.
[513.5.4] The column is oriented horizontally (![]() ),
i.e., perpendicular to the direction of gravity.
[513.5.5] The displacement processes are initiated by rotating
the column into a vertical position.
[513.5.6] The time protocol for rotating the column may
generally be written as
),
i.e., perpendicular to the direction of gravity.
[513.5.5] The displacement processes are initiated by rotating
the column into a vertical position.
[513.5.6] The time protocol for rotating the column may
generally be written as
| (14) |
where ![]() is the instant of most rapid rotation
and
is the instant of most rapid rotation
and ![]() is the inverse rate of the rotation.
is the inverse rate of the rotation.
[513.6.1] The constitutive equations yield the following system
of ![]() coupled nonlinear partial differential equations
coupled nonlinear partial differential equations
| (15a) | |||
| (15b) | |||
| (15c) | |||
| (15d) | |||
| (15e) | |||
| (15f) | |||
| (15g) | |||
| (15h) | |||
| (15i) | |||
| (15j) |
[page 514, §0]
where ![]() , and the
quantities
, and the
quantities ![]() ,
, ![]() are defined in eq. (7).
[514.0.1] This system of
are defined in eq. (7).
[514.0.1] This system of ![]() equations is reduced to a system
of only
equations is reduced to a system
of only ![]() equations by inserting eq. (15j) into
eqs. (15) and (15) to eliminate
equations by inserting eq. (15j) into
eqs. (15) and (15) to eliminate
![]() .
[514.0.2] The remaining
.
[514.0.2] The remaining ![]() unknowns are
unknowns are
![]() and
and ![]() .
.
[514.1.1] The system (15) has to be solved subject to initial and boundary data. [514.1.2] No flow boundary conditions at both ends require
| (16a) | |||
| (16b) |
[514.1.3] The fluids are incompressible. [514.1.4] Hence the reference pressure can be fixed to zero at the left boundary
| (17) |
[514.1.5] The saturations remain free at the boundaries of the column.
[514.2.1] Initially the fluids are at rest and their velocities vanish.
[514.2.2] The initial conditions are (![]() )
)
| (18a) | |||
| (18b) | |||
| (18c) |
[514.2.3] In the present study the initial saturations will
be taken as constants, i.e. independent of ![]() .
.
[514.3.1] The model parameters are chosen largely identical
to the parameters in [26].
[514.3.2] They describe experimental data obtained at the
Versuchseinrichtung zur Grundwasser- und
Altlastensanierung (VEGAS) at the Universität Stuttgart [40].
[514.3.3] The model parameters are
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
[514.3.4] In [26] only stationary and quasistationary
solutions were considered, and the viscous resistance
coefficients remained unspecified.
[514.3.5] In order to
[page 515, §0]
find realistic values remember that
.
[514.3.4] In [26] only stationary and quasistationary
solutions were considered, and the viscous resistance
coefficients remained unspecified.
[514.3.5] In order to
[page 515, §0]
find realistic values remember that
![]() [25, 26].
[515.0.1] Realistic values for the viscosity and permeability are
[25, 26].
[515.0.1] Realistic values for the viscosity and permeability are
![]() kgm
kgm![]() s
s![]() and
and ![]() m
m![]() .
[515.0.2] Based on these orders of magnitude the viscous resistance
coefficients are specified as
.
[515.0.2] Based on these orders of magnitude the viscous resistance
coefficients are specified as
![]() kg m
kg m![]() s
s![]() ,
and
,
and ![]() kg m
kg m![]() s
s![]() .
.
[515.1.1] The column is filled with water having total saturation
![]() and oil with saturation
and oil with saturation ![]() .
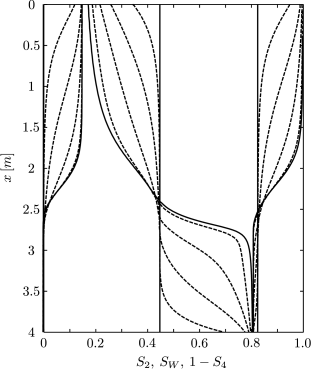
[515.1.2] Two different initial conditions will be investigated
that differ in relative abundance of the nonpercolating phase.
[515.1.3] The saturations for initial condition A and B are
in obvious notation given as
.
[515.1.2] Two different initial conditions will be investigated
that differ in relative abundance of the nonpercolating phase.
[515.1.3] The saturations for initial condition A and B are
in obvious notation given as
| (19a) | |||||
| (19b) | |||||
| (19c) | |||||
| (19d) |
[515.2.1] These phase distributions can be prepared experimentally
by an imbibition process for A or by a drainage process for
inital condition B.
[515.2.2] The values for the nonpercolating saturations were chosen
from the nonpercolating saturations predicted
within the residual decoupling approximation.
[515.2.3] They can be read off from Figure 5 in [26].
[515.2.4] The values for the percolating phases follow from the
requirement that the total water saturation is ![]() .
[515.2.5] The time scales for raising the column are chosen as
.
[515.2.5] The time scales for raising the column are chosen as
![]()
![]() corresponding to roughly 3 hours.
corresponding to roughly 3 hours.
 |
 |