Sie sind hier: ICP » R. Hilfer » Publikationen

5 Results

[515.5.1] Figures 2 show the time evolution of the saturation profile starting from initial condition A (left figure) and initial condition B (right figure). [515.5.2] Time instants shown are t=0s, t=6\times 10^{6}s (solid lines) [page 516, §0]    as well as t=10^{5}s, t=2.5\times 10^{5}s, t=5\times 10^{5}s and t=10^{6}s (dashed lines). [516.0.1] Gravity is oriented downward along the ordinate. [516.0.2] A complete saturation profile consists of three curves. [516.0.3] The leftmost curve of a triple is S_{2}(x,t), the middle curve is {S_{{\mathbb{W}}}}(x,t) and the rightmost curve is 1-S_{4}(x,t). [516.0.4] From these curves the saturations are easily read off using eq. (1b). [516.0.5] Namely, at fixed height x the distance from the ordinate to the first curve of a triple represents S_{2}(x), the distance between the first and the second curve represents S_{1}(x), the distance between the second and the third represents S_{3}(x) and the distance between the third curve and 1 represents S_{4}(x). [516.0.6] The initial saturations at t=0 correspond to vertical straight lines. [516.0.7] Subsequent profiles at t=10^{5},2.5\times 10^{5},5\times 10^{5} and 7.5\times 10^{5} s are represented by four triples of dashed curves. [516.0.8] The final quasistationary profile at t=6\times 10^{6}s is represented by one triple of solid curves.

[516.1.1] At t=0 the column is oriented horizontally, at t=10^{5}s the column has just reached its vertical position. [516.1.2] As the water begins to imbibe the lower part of the column the upper part is simultaneously drained. [516.1.3] As the oil rises upward it merges with the residual oil and creates irreducible water (left figure). [516.1.4] Equivalently the process may be viewed as leaving behind residual oil (see the lower right corner of the right figure). [516.1.5] Similarly, the water falling to the bottom may be viewed as leaving behind irreducible water (see the upper left corner of the left figure), or as merging with the irreducible water thereby creating residual oil as seen in the right figure. [516.1.6] Note also that in the region around x=2.5m the process can change with time from drainage to imbibition. [516.1.7] Therefore, in the process of raising a closed column the nature of the displacement (imbibition vs. drainage) is not only position but also timedependent.

[page 517, §1]    [517.2.1] Figure 3 compares the quasistationary (t=6\times 10^{6}s) saturation profiles for different initial conditions. [517.2.2] Dashed lines and curves correspond to initial condition A in eq. (19), while solid lines and curves show results for initial condition B. [517.2.3] The straight vertical line at 0.45 is a double line. [517.2.4] It represents the initial water saturation of 0.45 for both initial conditions. [517.2.5] Figure 3 shows a strong dependence on the initial distribution of nonpercolating fluids. [517.2.6] In particular the nonpercolating nonwetting fluid depends strongly on the initial condition. [517.2.7] Initial condition A represents a fluid distribution that could ensue after an imbibition, while initial condition B could be realistic after a drainage.

[517.3.1] Figure 4 illustrates the differences between the present theory and the traditional theory. [517.3.2] It shows the two quasistationary profiles (solid and dashed middle curves) as in Figure 3 calculated dynamically from the present theory and compares them to stationary solutions of the traditional theory based on the capillary pressure concept. [517.3.3] In the traditional theory the water saturation in hydrostatic equilibrium in a vertical column is given as [5]

{S_{{\mathbb{W}}}}(x)=P_{{\rm c}}^{{-1}}(C+(\varrho _{{\mathbb{O}}}-\varrho _{{\mathbb{W}}})gx) (20)

where P_{{\rm c}} is the capillary pressure and C an integration constant. [517.3.4] In view of the boundary conditions (closed column) the integration constant is fixed such that

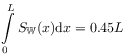\int\limits _{0}^{L}{S_{{\mathbb{W}}}}(x){\rm d}x=0.45L (21)

[page 518, §0]    is the total water volume. [518.0.1] The dash-dotted curve in Figure 4 is obtained in this way by specifying for P_{{\rm c}} the appropriate secondary drainage curve for the porous medium. [518.0.2] This secondary drainage curve was obtained in [26] and can be seen in Figure 1 of [26]. [518.0.3] The dotted curve in Figure 4 is obtained by specifying for P_{{\rm c}} the secondary imbibition curve for the medium. [518.0.4] This imbibition curve can be seen also in Figure 1 of [26]. [518.0.5] The comparison shows that the quasistationary solutions obtained from eqs. (15) differ significantly in the region of the capillary fringe from the equilibrium profiles predicted by the traditional theory.