3 Balance Laws

[143.1.1] Let $V=V_{\mathbb{S}}$ denote the sample volume, $V_{\mathbb{P}}$ denote the volume of pore space, $V_{\mathbb{W}}$ the volume filled with water, $V_{\mathbb{O}}$ the volume filled with oil, $V_{\mathbb{M}}=V_{5}$ the volume occupied by matrix, and $V_{i}=V_{{\mathbb{F}_{i}}}$ the volumes of the subsets $\mathbb{F}_{i}\subset\mathbb{S},i=1,2,3,4$ . [143.1.2] The volumes are defined as

$V_{\mathbb{G}}=\int\limits _{{\mathbb{R}^{3}}}\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{G}}}(\mathbf{y}){\rm d}^{3}\mathbf{y}$

(3)

where $i=\mathbb{F}_{1},\mathbb{F}_{2},\mathbb{F}_{3},\mathbb{F}_{4},\mathbb{S},\mathbb{P},\mathbb{M},\mathbb{W},\mathbb{O}$ , and

$\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{G}}}(\mathbf{y})=\begin{cases}1,&\mathbf{y}\in\mathbb{G}\\ 0,&\mathbf{y}\notin\mathbb{G}\end{cases}$

(4)

is the characteristic function of a set $\mathbb{G}$ . [143.1.3] Then volume conservation implies

$\displaystyle V_{\mathbb{S}}$	$\displaystyle=V=V_{\mathbb{P}}+V_{\mathbb{M}}=V_{\mathbb{W}}+V_{\mathbb{O}}+V_{\mathbb{M}}=\sum _{{i=1}}^{5}V_{i}$	(5a)
$\displaystyle V_{\mathbb{W}}$	$\displaystyle=V_{1}+V_{2}$	(5b)
$\displaystyle V_{\mathbb{O}}$	$\displaystyle=V_{3}+V_{4}$	(5c)

where $V_{5}=V_{\mathbb{M}}$ . [page 144, §0] [144.0.1] The volume fraction $\phi=V_{\mathbb{P}}/V$ is called total or global porosity. [144.0.2] The volume fraction $V_{\mathbb{W}}/V_{\mathbb{P}}=(V_{\mathbb{W}}/V)/\phi$ is the total or global water saturation, and analogous intensive quantities can be defined for the other phases.

[144.1.1] Often the saturations are not constant but vary on macroscopic scales. [144.1.2] Local volume fractions are defined by introducing a one parameter family of functions $X^{\varepsilon}_{\mathbb{G}}\colon\mathbb{R}^{3}\times\mathbb{R}^{3}\to\mathbb{R}$ by defining $X^{1}(\mathbf{x},\mathbf{x})=\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{G}}}(\mathbf{x})$ on the diagonal and then extending it as

$X_{\mathbb{G}}^{\varepsilon}(\mathbf{x},\mathbf{y})=X_{\mathbb{G}}^{1}(\mathbf{x},\mathbf{x}/\varepsilon)$

(6)

to the full space. [144.1.3] Here $\varepsilon>0$ is the scale separation parameter, and $\mathbf{y}=\mathbf{x}/\varepsilon$ is the fast variable. [144.1.4] For an infinite sample $\mathbb{S}=\mathbb{R}^{3}$ the local volume fractions may be defined as

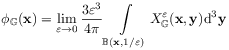$\phi _{\mathbb{G}}(\mathbf{x})=\lim _{{\varepsilon\to 0}}\frac{3\varepsilon^{3}}{4\pi}\int\limits _{{\mathbb{B}(\mathbf{x},1/\varepsilon)}}X^{\varepsilon}_{\mathbb{G}}(\mathbf{x},\mathbf{y}){\rm d}^{3}\mathbf{y}$

(7)

where $\mathbb{G}=\mathbb{F}_{1},\mathbb{F}_{2},\mathbb{F}_{3},\mathbb{F}_{4},\mathbb{S},\mathbb{P},\mathbb{M},\mathbb{W},\mathbb{O}$ , and $\mathbb{B}(\mathbf{x},1/\varepsilon)$ is a sphere of radius $1/\varepsilon$ centered at $\mathbf{x}$ with volume $4\pi/(3\varepsilon^{3})$ . [144.1.5] In the following it is assumed that the limit exists, but may in general depend also on time so that the local volume fractions $\phi _{i}(\mathbf{x},t)$ become position and time dependent. [144.1.6] Local volume conservation implies the relations

$\displaystyle\phi _{1}+\phi _{2}+\phi _{3}+\phi _{4}+\phi _{5}$	$\displaystyle=1$	(8a)
$\displaystyle S_{1}+S_{2}+S_{3}+S_{4}$	$\displaystyle=1$	(8b)
$\displaystyle 1-\phi$	$\displaystyle=\phi _{5}$	(8c)

where $\phi _{i}=\phi S_{i}$ $(i=1,2,3,4)$ are volume fractions, and $S_{i}$ are saturations. [144.1.7] The water saturation is defined as ${S_{{\mathbb{W}}}}=S_{1}+S_{2}$ , and the oil saturation as ${S_{{\mathbb{O}}}}=1-{S_{{\mathbb{W}}}}=S_{3}+S_{4}$ .

[144.2.1] The general law of mass balance in differential form reads ( $i=1,2,3,4$ )

$\frac{\partial(\phi _{i}\varrho _{i})}{\partial t}+\mathbf{\nabla}\cdot(\phi _{i}\varrho _{i}{\mathbf{v}}_{i})=M_{i}=\sum _{{j=1}}^{5}M_{{ij}}$

(9)

where $\varrho _{i}(\mathbf{x},t),\phi _{i}(\mathbf{x},t),{\mathbf{v}}_{i}(\mathbf{x},t)$ denote mass density, volume fraction and velocity of phase $i=\mathbb{W},\mathbb{O}$ as functions of position $\mathbf{x}\in\mathbb{S}\subset\mathbb{R}^{3}$ and time $t\in\mathbb{R}_{+}$ . [144.2.2] Exchange of mass between the two phases is described by mass transfer rates $M_{i}$ giving the amount of mass by which phase $i$ changes per unit time and volume. [144.2.3] The rate $M_{{ij}}$ is the rate of mass transfer from phase $j$ into phase $i$ .

[144.3.1] The law of momentum balance is formulated as ( $i=1,2,3,4$ )

$\phi _{i}\varrho _{i}\frac{{\rm D}^{i}}{{\rm D}t}{\mathbf{v}}_{i}-\phi _{i}\mathbf{\nabla}\cdot\Sigma _{i}-\phi _{i}\mathbf{F}_{i}=\mathbf{m}_{i}-{\mathbf{v}}_{i}M_{i}$

(10)

where $\Sigma _{i}$ is the stress tensor in the $i$ th phase, $\mathbf{F}_{i}$ is the body force per unit volume acting on the $i$ th phase, $\mathbf{m}_{i}$ is the momentum transfer into phase $i$ from all the other phases, and

$\frac{{\rm D}^{i}}{{\rm D}t}=\frac{\partial}{\partial t}+{\mathbf{v}}_{i}\cdot\mathbf{\nabla}$

(11)

denotes the material derivative for phase $i=\mathbb{W},\mathbb{O}$ .

Author:	R. Hilfer
from:	...
originally submitted:	2009