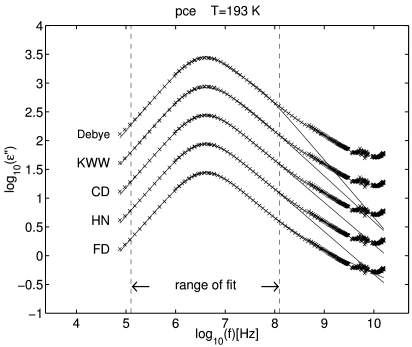
Sie sind hier: ICP » R. Hilfer » Publikationen

3 Fractional dynamics (FD) and excess wings

[123.6.1] The theory of fractional dynamics yields a three parameter function, that allows to fit both, the asymmetric peak and the excess wing with a single stretching exponent [17, 16, 23]. [123.6.2] The three parameter function is denoted as “fractional dynamics” (FD) relaxation in figure 2. [123.6.3] Its functional form reads

\displaystyle f(t) \displaystyle=\mathrm{E}_{{(1,1-\alpha),1}}\left(-\frac{t}{\tau _{1}},-\frac{\tau _{2}^{\alpha}}{\tau _{1}}t^{{1-\alpha}}\right) (8a)
\displaystyle\varepsilon(u) \displaystyle=\frac{1+(u\tau _{2})^{\alpha}}{1+(u\tau _{2})^{\alpha}+u\tau _{1}} \displaystyle\text{(FD)}. (8b)

where

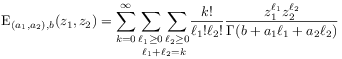\mathrm{E}_{{(a_{1},a_{2}),b}}(z_{1},z_{2})=\sum _{{k=0}}^{\infty}\underset{\ell _{1}+\ell _{2}=k}{\sum _{{\ell _{1}\geq 0}}\sum _{{\ell _{2}\geq 0}}}\frac{k!}{\ell _{1}!\ell _{2}!}\frac{z_{1}^{{\ell _{1}}}z_{2}^{{\ell _{2}}}}{\Gamma(b+a_{1}\ell _{1}+a_{2}\ell _{2})} (9)

with a_{1},a_{2}>0 and b,z_{1},z_{2}\in\mathbb{C} is the binomial Mittag-Leffler function [25]. [123.6.4] The function f(t) from eq. (8) solves the fractional differential equation

\tau _{1}\frac{\mathrm{d}f}{\mathrm{d}t}+\tau _{2}^{\alpha}\mathrm{A}_{\alpha}f=-f (10)

with \tau _{1},\tau _{2}>0, 0<\alpha<1, and inital value f(0)=1 [25]. [123.6.5] In eq. (10) the operator \mathrm{A}_{\alpha} is the infinitesimal generator of fractional time evolutions of index \alpha [7, 11, 10, 9, 15, 23]. [123.6.6] It can be written as a fractional time derivative of order \alpha in the form

\mathrm{A}_{\alpha}=-\left(-\mathrm{A}\right)^{\alpha}=-\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)^{\alpha} (11)

where \mathrm{A}=-\mathrm{d}/\mathrm{d}t is the infinitesimal generator of translations. [123.6.7] For a mathematical definition of \mathrm{A}_{\alpha} see [23]. [123.6.8] Note, that the solution (8) of eq. (10) holds also for generalized Riemann-Liouville operators \mathrm{A}_{\alpha}=\mbox{\rm D}^{{\alpha,\gamma}}_{{0+}} of order \alpha and type 0<\gamma<1 as shown in [17, 16]. [123.6.9] The (right-/left-sided) generalized Riemann-Liouville fractional derivative of order 0<\alpha<1 and type 0\leq\gamma\leq 1 with respect to x was introduced in definition 3.3 in [15, p.113] by

\mbox{\rm D}^{{\alpha,\gamma}}_{{a\pm}}f(x)=\left(\pm\mbox{\rm I}^{{\gamma(1-\alpha)}}_{{a\pm}}\frac{\mathrm{d}}{\mathrm{d}x}(\mbox{\rm I}^{{(1-\gamma)(1-\alpha)}}_{{a\pm}}f)\right)(x) (12)

where

(\mbox{\rm I}^{{\alpha}}_{{a+}}f)(x)=\frac{1}{\Gamma(\alpha)}\int _{a}^{x}(x-y)^{{\alpha-1}}f(y)\;\mathrm{d}y (13)

for x>a, denotes the right-sided Riemann-Liouville fractional integral of order \alpha>0, and the left sided integral \mbox{\rm I}^{{\alpha}}_{{a-}} is defined analogously [15, 13].

Figure 2: Five different fits to the imaginary part Im\varepsilon(u) (u=-2\pi\text{i}\nu) of the complex dielectric function of propylene carbonate at T=193K as a function of frequency. Experimental data represented by crosses are taken from Ref. [34]. The range over which the data were fitted is indicated by dashed vertical lines in the figure. For clarity the data were displaced vertically by half a decade each. The original location of the data corresponds to the curve labelled FD.