Appendix

[123.8.1] The $H$ -function of order $(m,n,p,q)\in\mathbb{N}^{4}$ and with parameters $A_{i}\in\mathbb{R}_{+}(i=1,\ldots,p)$ , $B_{i}\in\mathbb{R}_{+}(i=1,\ldots,q)$ , $a_{i}\in\mathbb{C}(i=1,\ldots,p)$ , and $b_{i}\in\mathbb{C}(i=1,\ldots,q)$ is defined for $z\in\mathbb{C},z\neq 0$ by the contour integral [5, 32]

$H^{{m,n}}_{{p,q}}\left(z\left|\begin{array}[]{l}{(a_{1},A_{1}),\ldots,(a_{p},A_{p})}\\ {(b_{1},B_{1}),\ldots,(b_{q},B_{q})}\end{array}\right.\right)=\frac{1}{2\pi i}\int _{{\mathcal{L}}}\eta(s)z^{{-s}}\;\mathrm{d}s$

(14)

where the integrand is

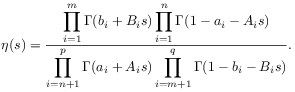$\eta(s)=\frac{\displaystyle\prod _{{i=1}}^{m}\Gamma(b_{i}+B_{i}s)\prod _{{i=1}}^{n}\Gamma(1-a_{i}-A_{i}s)}{\displaystyle\prod _{{i=n+1}}^{p}\Gamma(a_{i}+A_{i}s)\prod _{{i=m+1}}^{q}\Gamma(1-b_{i}-B_{i}s)}.$

(15)

[123.8.2] In (14) $z^{{-s}}=\exp\{-s\log|z|-i\arg z\}$ and $\arg z$ is not necessarily the principal value. [123.8.3] The integers $m,n,p,q$ must satisfy

$0\leq m\leq q,\qquad 0\leq n\leq p,$

(16)

and empty products are interpreted as being unity. [123.8.4] For the conditions on the other parameters and the path ${\mathcal{L}}$ of integration the reader is referred to the literature [5] (see [13, p.120ff] for a brief summary).

Author:	R. Hilfer
originally published in:	Recent Advances in Broadband Dielectric Spectroscopy, Springer, Netherlands, pages 123-130 (2012), ISBN 978-94-007-5011-1
originally published:	August 21st, 2012