Sie sind hier: ICP » R. Hilfer » Publikationen

3 Results

[page 4, §1]   
[4.1.1] It follows from the general results in Ref. [1] that the first model defined by eqs. (6) and (9) is equivalent to the fractional master equation

\mbox{\rm D}^{{\alpha,1}}_{{0+}}p(\mathbf{r},t)=\sum _{{\mathbf{r}^{\prime}}}w(\mathbf{r}-\mathbf{r}^{\prime})p(\mathbf{r}^{\prime},t) (10)

with intitial condition

p(\mathbf{r},0)=\delta _{{\mathbf{r},\mathbf{0}}} (11)

and fractional transition rates

w(\mathbf{r})=\frac{\lambda(\mathbf{r})-1}{\tau^{\alpha}}. (12)

Here the fractional time derivative \mbox{\rm D}^{{\alpha,1}}_{{0+}} of order \alpha and type 1 in eq. (10) is defined as [15]

\mbox{\rm D}^{{\alpha,1}}_{{0+}}p(\mathbf{r},t)=\frac{1}{\Gamma(1-\alpha)}\int _{0}^{t}(t-t^{\prime})^{{-\alpha}}\frac{\partial}{\partial t}p(\mathbf{r},t^{\prime}){\mathrm{d}}t^{\prime} (13)

thereby giving a more precise meaning to the symbolic notation in eq. (1).

[page 5, §1]    [5.1.1] The result is obtained from inserting the Laplace transform of \psi _{1}(t)

\psi _{1}(u)=\frac{1}{1+(\tau u)^{\alpha}} (14)

and the Fourier transform of \lambda(\mathbf{r}), the so called structure function

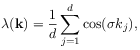\lambda(\mathbf{k})=\frac{1}{d}\sum _{{j=1}}^{d}\cos(\sigma k_{j}), (15)

into eq. (5). [5.1.2] This gives

p_{1}(\mathbf{k},u)=\frac{1}{u}\left(\frac{(\tau u)^{\alpha}}{1+(\tau u)^{\alpha}-\lambda(\mathbf{k})}\right)=\frac{u^{{\alpha-1}}}{u^{\alpha}-w(\mathbf{k})} (16)

where the Fourier transform of eq. (12) was used in the last equality and the subscript refers to the first model. [5.1.3] Equation (16) equals the result obtained from Fourier-Laplace transformation of the fractional Cauchy problem defined by equations (10) and (11). [5.1.4] Hence a CTRW-model with \psi _{1}(t) and the fractional master equation describe the same random walk process in the sense that their fundamental solutions are the same.

[5.2.1] The continuum limit \sigma,\tau\to 0 was the background and motivation for the discussion in Ref. [2]. [5.2.2] It follows from eq. (1.9) in Ref. [2] by virtue of the continuity theorem [16] for characteristic functions that for the first model the continuum limit with

C_{\alpha}=\lim _{{\substack{\tau\to 0\\ \sigma\to 0}}}\frac{\sigma}{2d\tau^{\alpha}} (17)

leads for all fixed \mathbf{k},u to

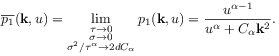\overline{p_{1}}(\mathbf{k},u)=\lim _{{\substack{\tau\to 0\\ \sigma\to 0\\ \sigma^{2}/\tau^{\alpha}\to 2dC_{\alpha}}}}p_{1}(\mathbf{k},u)=\frac{u^{{\alpha-1}}}{u^{\alpha}+C_{\alpha}\mathbf{k}^{2}}. (18)

[5.2.3] Here the expansion \cos(x)=1-x^{2}/2+x^{4}/24-... has been used. [5.2.4] Therefore the solution of the first model with waiting time density \psi _{1}(t) converges in the continuum limit to the solution of the fractional diffusion equation

\mbox{\rm D}^{{\alpha,1}}_{{0+}}\overline{p_{1}}(\mathbf{r},t)=C_{\alpha}\Delta\overline{p_{1}}(\mathbf{r},t) (19)

with initial condition analogous to eq. (11).

[5.3.1] Consider now the second model with waiting time density \psi _{2}(t) given by eq. (8). [5.3.2] In this case

\psi _{2}(u)=\frac{1}{2+2c\tau^{2}u^{\alpha}}+\frac{1}{2+2\tau u} (20)

and

\displaystyle p_{2}(\mathbf{k},u) \displaystyle=\frac{1}{u}\left(1-(\lambda(\mathbf{k})-1)\frac{\psi _{2}(u)}{1-\psi _{2}(u)}\right)^{{-1}}
\displaystyle=\frac{1}{u}\left(1-(\lambda(\mathbf{k})-1)\frac{2+\tau u+c\tau^{2}u^{\alpha}}{\tau u+c\tau^{2}u^{\alpha}+2c\tau^{3}u^{{\alpha+1}}}\right)^{{-1}} (21)
\displaystyle=\frac{1}{u}\left\{ 1+\frac{1}{\tau^{\alpha}u^{\alpha}}\left(\frac{\sigma^{2}\mathbf{k}^{2}}{2d}-\frac{\sigma^{4}\mathbf{k}^{4}}{24d}+...\right)\left(\frac{2+\tau u+c\tau^{2}u^{\alpha}}{(\tau u)^{{1-\alpha}}+c\tau^{{2-\alpha}}+2c\tau^{{3-\alpha}}u}\right)\right\}^{{-1}}.

From this follows

\overline{p_{2}}(\mathbf{k},u)=\lim _{{\substack{\tau\to 0\\ \sigma\to 0\\ \sigma^{2}/\tau^{\alpha}\to 2dC_{\alpha}}}}p_{2}(\mathbf{k},u)=0 (22)

showing that the continuum limit as in eq. (17) with finite C_{\alpha} does not give rise to the propagator of fractional diffusion. [5.3.3] On the other hand the conventional continuum limit with C_{1}=\lim _{{\substack{\tau\to 0\\ \sigma\to 0}}}\sigma^{2}/(2d\tau) exists and yields

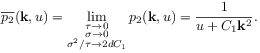\overline{p_{2}}(\mathbf{k},u)=\lim _{{\substack{\tau\to 0\\ \sigma\to 0\\ \sigma^{2}/\tau\to 2dC_{1}}}}p_{2}(\mathbf{k},u)=\frac{1}{u+C_{1}\mathbf{k}^{2}}. (23)

the Gaussian propagator of ordinary diffusion with diffusion constant C_{1}.