Sie sind hier: ICP » R. Hilfer » Publikationen

2 Definition of Models

[2.3.1] Consider first the integral equation of motion for the CTRW-model [9, 10]. [2.3.2] The probability density p(\mathbf{r},t) obeys the integral equation

p(\mathbf{r},t)=\delta _{{\mathbf{r}0}}\Phi(t)+\int _{0}^{t}\psi(t-t^{\prime})\sum _{{\mathbf{r}^{\prime}}}\lambda(\mathbf{r}-\mathbf{r}^{\prime})p(\mathbf{r}^{\prime},t^{\prime})\, dt^{\prime} (3)

where \lambda(\mathbf{r}) denotes the probability for a displacement \mathbf{r} in each single step, and \psi(t) is the waiting time distribution giving the probability density for the time interval t between two consecutive steps. [2.3.3] The transition probabilities obey \sum _{{\mathbf{r}}}\lambda(\mathbf{r})=1, and the function \Phi(t) is the survival probability at the initial position which is related to the waiting time distribution through

\Phi(t)=1-\int _{0}^{t}\psi(t^{\prime})\, dt^{\prime}. (4)

[page 3, §0]   Fourier-Laplace transformation leads to the solution in Fourier-Laplace space given as [10]

p(\mathbf{k},u)=\frac{1}{u}\frac{1-\psi(u)}{1-\psi(u)\lambda(\mathbf{k})} (5)

where p(\mathbf{k},u) is the Fourier-Laplace transform of p(\mathbf{r},t) and similarly for \psi and \lambda.

[3.1.1] Two lattice models with different waiting time density will be considered. [3.1.2] In the first model the waiting time density is chosen as the one found in [1, 2]

\psi _{1}(t)=\frac{t^{{\alpha-1}}}{\tau^{{\alpha}}}E_{{\alpha,\alpha}}\left(-\frac{t^{\alpha}}{\tau^{\alpha}}\right), (6)

where 0<\alpha\leq 1,0<\tau<\infty is the characteristic time, and

E_{{a,b}}(x)=\sum _{{k=0}}^{\infty}\frac{x^{k}}{\Gamma(ak+b)}\qquad a>0,b\in\mathbb{C}. (7)

is the generalized Mittag-Leffler function [14]. [3.1.3] In the second model the waiting time density is chosen as

\psi _{2}(t)=\frac{t^{{\alpha-1}}}{2c\tau^{2}}E_{{\alpha,\alpha}}\left(-\frac{t^{\alpha}}{c\tau^{2}}\right)+\frac{1}{2\tau}\exp(-t/\tau) (8)

where 0<\alpha\leq 1, 0<\tau<\infty and c>0 is a suitable dimensional constant.

[3.2.1] The waiting time density \psi _{2}(t) differs only little from \psi _{1}(t) as shown graphically in Figure 1.

Figure 1: Waiting time densities \psi _{1}(t) for model 1 and \psi _{2}(t) for model 2 with \alpha=0.8, \tau=1 s and c=1 s{}^{{-1.2}}.

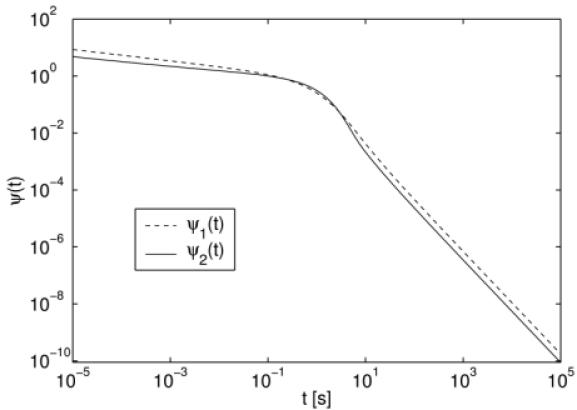
[3.2.2] Note that both models have a long time tail of the form given in eq. (2), and the average waiting time \int _{0}^{\infty}t\psi _{i}(t){\mathrm{d}}t diverges.

[3.3.1] For both models the spatial transition probabilities are chosen as those for nearest-neighbour transitions (Polya walk) on a d-dimensional hypercubic lattice given as

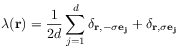\lambda(\mathbf{r})=\frac{1}{2d}\sum _{{j=1}}^{d}\delta _{{\mathbf{r},-\sigma\mathbf{e_{j}}}}+\delta _{{\mathbf{r},\sigma\mathbf{e_{j}}}} (9)

where \mathbf{e_{j}} is the j-th unit basis vector generating the lattice, \sigma>0 is the lattice constant and \delta _{{\mathbf{r},\mathbf{s}}}=1 for \mathbf{r}=\mathbf{s} and \delta _{{\mathbf{r},\mathbf{s}}}=0 for \mathbf{r}\neq\mathbf{s}.