Erstes Modell: Oszillatorgleichung

Nach so viel Programmieren wollen wir jetzt zur Physik zurückkehren. Ziel dieses Kapitels ist es, an einem einfachen Beispiel zu zeigen, wie der Computer heute in der Physik zum Modellieren eingesetzt wird. Es sollen dabei auch die Probleme solcher Modellierung aufgezeigt werden.

Als Beispiel wählen wir die schwingende Saite. Eine an beiden Enden eingespannte Saite (aus Kuhdarm, Plastik oder Metall) kann bekanntlich durch Zupfen oder Schlagen zu Schwingungen angeregt werden. Dies war bereits Pythagoras bekannt von dem berichtet wird, daß  er Wohlklang feststellte, wenn man eine Saite im Verhältnis kleiner ganzer Zahlen unterteilt (z.B. 1:2, 3:1, 3:2 usw.). Schwingende Saiten werden in vielen Musikinstrumenten wie etwa Gitarre oder Klavier zur Klangerzeugung genutzt. Wir stellen es uns deshalb als Aufgabe, den Klang einer schwingenden Gitarrensaite zu modellieren.

Ein erstes Modell der Gitarrensaite könnte aus der Beobachtung entstehen, daß  eine fest gewählter Punkt entlang der Saite regelmäßig auf und ab schwingt. Die Schwingungen ähneln denen eines harmonischen Oszillators, wie er in der Einleitung diskutiert wurde. Allerdings gibt es da noch ein Problem: Wenn die Saite einmal angezupft ist, und sich selbst überlassen bleibt, dann klingt die Schwingung mit der Zeit ab. Die Schwingung der Saite ist gedämpft, sie verliert Energie. Dies war beim harmonischen Oszillator in der Einleitung nicht der Fall. Wir müssen deshalb noch die Dämpfung modellieren. Dies könnte z.B. durch Einführung einer Reibungskraft geschehen.

Als Beispiel wählen wir eine (viskose) Reibungskraft $F_R=-b v$. Sie ist proportional zum Betrag der Geschwindigkeit $v=\dot x$ und ihr entgegengerichtet. Das führt dann auf die Bewegungsgleichung für den gedämpften harmonischen Oszillator

$$m\frac{\mbox{\rm d}^2x}{\mbox{\rm d}t^2}=-b\frac{\mbox{\rm d}x}{\mbox{\rm d}t} -kx .$$ (3.1)

(mit $-\infty<x,t<\infty$ und $m,k,b>0$) mit den Anfangsbedingungen

Wir können jetzt die Gleichung dimensionslos machen und alle Schritte wiederholen, die wir auch beim einfachen harmonischen Oszillator durchgeführt haben.

Das führt auf den Algorithmus analog zu Gleichung ()

wobei

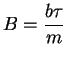$$B=\frac{b\tau}{m}$$ (3.4)

die dimensionlose Dämpfungskonstante ist.

Um die Qualität unseres einfachen Computermodells einer schwingenden Saite zu überprüfen, wollen wir das Ergebnis unserer Rechnung diesmal nicht anschauen, sondern anhören. Dies ist recht einfach, da die meisten Computer heutzutage multimediafähig sind und deshalb oft eine Klangkarte eingebaut haben. Voraussetzung für das Folgende ist also eine eingebaute und richtig konfigurierte Klangkarte (engl. sound card).

Wir wollen das Ergebnis der Rechnung als Klang in CD-Qualität hörbar machen. Das bedeutet, wir wählen als digitale Abtastrate $a=44100$Hz. Die Abtastrate oder Abtastfrequenz (engl.: sampling rate) gibt die Qualität der Diskretisierung des analogen Signals an. Ein Funktionsverlauf wird mit $a$ Stützpunkten pro Sekunde festgelegt. Für CD-Qualität benötigen wir $a=44100$ Funktionswerte pro Sekunde. Niedrigere Abtastraten bedeuten einen schlechteren Klang. In Telefonqualität benötigt man nur ca. $a=8000$ Werte pro Sekunde. Ausserdem wählen wir für die Diskretisierung der Funktion in $y$-Richtung (auf der Ordinate) den Variablentyp short int, der auf den meisten Computern 16 Bit entspricht. Man kann damit $2^{16}=65536$ Funktionswerte darstellen. Das bedeutet, daß  die maximale Amplitude $65536/2=32768$ beträgt. Wir müssen also in unserem Programm nur die Parameter geeignet wählen, das Ergebnis von double auf short umwandeln, und es im Binärformat abspeichern. Ein einfaches Programm, um den gedämpften harmonischen Oszillator hörbar zu machen, könnte also wie folgt aussehen.

/*********************************************************************
  gharmos.cc -- gedaempfter harmonischer Oszillator
  Autor    : R. Hilfer
  Zweck    : Beispiel zur Vorlesung, demonstriert iterative Loesung
             des ged. harm. Oszillators mit BGL u''=-Cu-Bu',
  Gebrauch : Eingabe von stdin: 
               frq = Frequenz in Hertz 
               t_max = Gesamtzeit
  Dateien  : Ausgabe auf Datei gharmos.raw in binaerem Format
             Umwandlung mit dem Befehl 
               sox -s -w -r 44100 gharmos.raw gharmos.wav
             in wav-Format
  Version  : 1.0 (Originalversion) erstellt am  12.10.2000
 *********************************************************************/

// Einbinden benoetigter Bibliotheken
#include<iostream>
using std::cin;
using std::cout;
#include<fstream>
using std::ostream;
#include<cmath>

int main()
{
// Deklarationen
   double u[2], v[2], t;  // u = Auslenkung, v=Geschwindigkeit, t=Zeit
   double C,omega,B;      // omega=Kreisfrequenz, B=Daempfung
   double u_0,v_0;        // u_0=Anfangsauslenkung, v_0=Anfangsgeschwindigkeit
   double t_max, dt;      // t_max=Gesamtzeit, dt=Zeitintervall
   double pi,frq;
   short amp;             // Amplitude in short fuer Ausgabe im raw Format

// Parameter abfragen und einlesen
   cout << "Frequenz :";  cin >> frq;
   cout << "Daempfungskonstante  > 1.     :";  cin >> B;
   if(B<0.1) {           // Sicherheitsprfg, damit nicht zu grosse Dateien
     cout << "-->FEHLER:\tB ist zu klein\n \t\tB groesser als 1. waehlen\n"; 
     return 3; 
   }

// Vorbereitungen 
   u_0 = 28000.;                   // Anfangsauslenkung setzen
   v_0 = 0.;                       // Anfangsgeschwindigkeit auf 0 setzen
   pi = acos(-1.);                 // Konstant pi berechnen
   omega = 2.*pi*frq;              // Kreisfrequenz
   C = omega*omega;                // Festlegung der Konstante C
   u[0]=u_0;                       // Initialisierungen der Variablen
   v[0]=v_0;
   t=0.0;
   t_max = 10./B;    // Zeitdauer = zehnfache Relaxationszeit
   dt = 1./44100.;                 // Abtastrate

//binaere Ausgabedatei outfile oeffnen
   ofstream outfile("gharmos.raw",ios::out|ios::binary); 

// Iterativer Algorithmus : Schleife von t=0 bis t=t_max
   for( int i=0; i<=t_max/dt; i++ )
   {
     v[1]=(1.-B*dt)*v[0]-C*u[0]*dt;
     u[1]=u[0]+v[1]*dt;       // Berechne u und v rekursiv
     amp = (int)u[0];         // Umwandlung zur Ausgbe in short
     outfile.write(&amp,2);   // binaere Ausgabe : 2 byte schreiben
     t=t+dt;              // Zeit weiterzaehlen
     u[0]=u[1];           // Variablen umsetzen fuer naechsten Schritt
     v[0]=v[1];
   }

//binaere Ausgabedatei outfile schliessen
   outfile.close();
// Ende des Hauptprogramms
}

Sobald die Binärdatei erzeugt ist, übernehmen bereits vorhandene Werkzeuge den Rest. Die abgespeicherte Datei wird mit dem Kommando

sox -s -w -r 44100 gharmos.raw gharmos.wav

in eine auf Datei im sogenannten wav-Format umgewandelt, die auf den meisten Rechnern abspielbar ist. Wir könnten die Daten auch in das Dateiformat für CD's umwandeln und dann auf CD brennen, um das Ergebnis auf jedem handelsüblichen CD-Spieler anzuhören.