Um die Lösung ![]() unseres Problems in (
unseres Problems in (![]() )
numerisch zu berechnen führen wir die Hilfsgröße
)
numerisch zu berechnen führen wir die Hilfsgröße
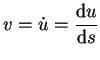 |
(1.20) |
Natürlich ist ![]() die dimensionslose Geschwindigkeit.
Nun erinnern wir uns an die Definition der 1. Ableitung
die dimensionslose Geschwindigkeit.
Nun erinnern wir uns an die Definition der 1. Ableitung
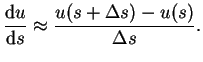 |
(1.23) |
Nun erkennen wir einen numerischen Algorithmus zur Lösung,
denn dies ist eine Rekursionsbeziehung.
Mit Hilfe von ![]() können wir
können wir
![]() aus
der Kenntnis von
aus
der Kenntnis von ![]() berechnen.
Da wir auch
berechnen.
Da wir auch
![]() aus
aus ![]() und
und ![]() berechnen können
läßt sich das Vorgehen iterieren, um
berechnen können
läßt sich das Vorgehen iterieren, um
![]() zu berechnen, und dann
zu berechnen, und dann
![]() und so weiter.
Allerdings hat dieser Algorithmus einen Nachteil,
er ist instabil.
Eine kleine Änderung behebt diesen Defekt.
Wir berechnen zunächst die Hilfsgröße
und so weiter.
Allerdings hat dieser Algorithmus einen Nachteil,
er ist instabil.
Eine kleine Änderung behebt diesen Defekt.
Wir berechnen zunächst die Hilfsgröße
![]() zur Zeit
zur Zeit
![]() und verwenden
dann diesen Wert zur Berechnung der Auslenkung
und verwenden
dann diesen Wert zur Berechnung der Auslenkung
![]() .
Damit wird aus (
.
Damit wird aus (![]() ) der Algorithmus
) der Algorithmus
den wir nachfolgend als Computerprogramm implementieren wollen.