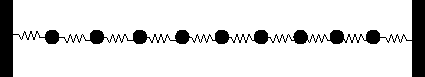 |
Eine Verbesserung des Modells könnte darin bestehen, nicht nur einen Punkt auf der Saite durch einen harmonischen Oszillator zu modellieren, sondern mehrere, und dann diese Oszillatoren miteinander zu koppeln. Das führt zu dem Modell einer Kette von gekoppelten harmonischen Oszillatoren, so wie in der Abbildung dargestellt.
Dieses Modell kommt der Wirklichkeit schon wesentlich
näher, wenn man hinreichend viele Oszillatoren koppelt.
Im Limes
![]() von unendlich vielen
infinitesimal benachbarten Oszillatoren führt es
auf ein Modell für die Saite mit einer kontinuierlichen
Masseverteilung entlang der Saite.
Betrachten wir also eine gespannte Saite mit konstanter
Massendichte
von unendlich vielen
infinitesimal benachbarten Oszillatoren führt es
auf ein Modell für die Saite mit einer kontinuierlichen
Masseverteilung entlang der Saite.
Betrachten wir also eine gespannte Saite mit konstanter
Massendichte ![]() und Querschnittsfläche
und Querschnittsfläche ![]() .
Die Saite sei durch eine Kraft
.
Die Saite sei durch eine Kraft ![]() an beiden Enden
eingespannt, und sie soll nur transversal in einer
festen Richtung ausgelenkt werden können.
an beiden Enden
eingespannt, und sie soll nur transversal in einer
festen Richtung ausgelenkt werden können.
Die Auslenkung der Saite ![]() ist eine Funktion der
Zeit
ist eine Funktion der
Zeit ![]() und der Ortskoordinate
und der Ortskoordinate ![]() entlang der Saite.
Betrachten wir die Kräfteverhältnisse entlang d. Saite:
entlang der Saite.
Betrachten wir die Kräfteverhältnisse entlang d. Saite:
Wir fragen nach der Rückstellkraft entlang der u-Richtung (Ordinate), für die offenbar gilt:
| (3.5) |
nun ist im allgemeinen die Auslenkung ![]() Länge
der Saite. Daraus folgt, dass
Länge
der Saite. Daraus folgt, dass
![]() , d. h.
, d. h. ![]() ist klein, und mit
ist klein, und mit
![]() :
:
| (3.6) |
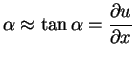 |
(3.7) |
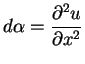 |
(3.8) |
| (3.9) |
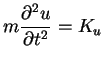 |
(3.10) |
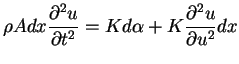 |
(3.11) |
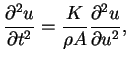 |
(3.12) |
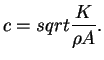 |
(3.14) |
Natürlich gehören zu einer sauberen Problemformulierung auch Anfangs- und
Randbedingungen. Diese wählen wir hier wie folgt:
Als Anfangsbedingungen: