Betrachte
![]() d.h. die ganze reelle Achse.
Zunächst berechnen wir aus
d.h. die ganze reelle Achse.
Zunächst berechnen wir aus
![]() , dass die Gleichung
, dass die Gleichung
![]() eine
wichtige Rolle spielt. Wir verwenden wegen
eine
wichtige Rolle spielt. Wir verwenden wegen
![]() die Substitution:
die Substitution:
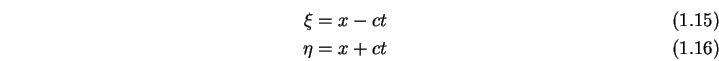
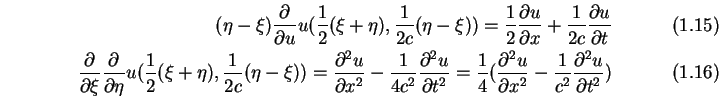
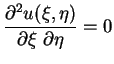 |
(3.15) |
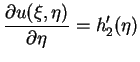 |
(3.16) |
| (3.17) |
mit einer Konstanten ![]() .
Aus Addition und Subtraktion von (
.
Aus Addition und Subtraktion von (![]() ) und
(
) und
(![]() ) gilt
) gilt
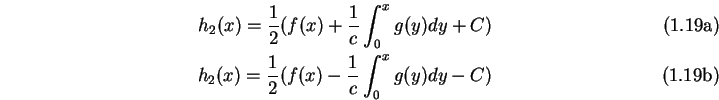
Also folgt
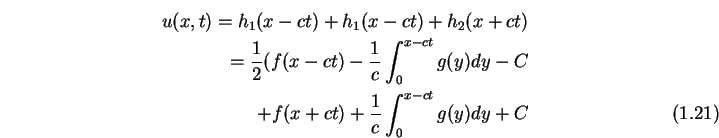
Im Spezialfall ![]() folgt dann
folgt dann
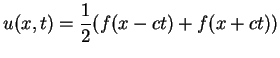 |
(3.22) |
d.h die Auslenkung zerfällt in zwei identische Pulse, die sich in entgegengesetzte Richtung ausbreiten.
Wir betrachten nun den Einfluß der Randbedingungen, d.h.
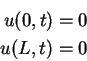 Natürlich sind dann die Anfangsbedingungen auch nur für
Natürlich sind dann die Anfangsbedingungen auch nur für
![]() von Interesse. Gleichung (
von Interesse. Gleichung (![]() ) zeigt, dass dann
) zeigt, dass dann
![]() für
für
![]() definiert sein muss und
definiert sein muss und ![]() für
für
![]() .
Man erhält dann
.
Man erhält dann
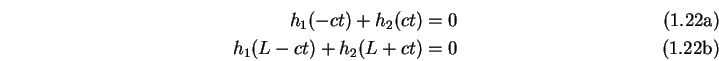
oder mit ![]() bzw.
bzw.
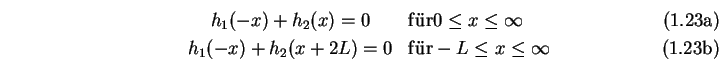
Setzt man ![]() aus der ersten Gleichung in die zweite ein so folgt
aus der ersten Gleichung in die zweite ein so folgt
| (3.25) |
| (3.26) |
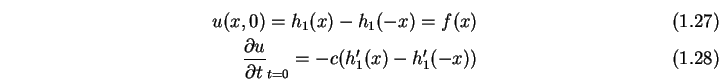
Die allgemeine Lösung des Rand- und Anfangswertproblems ist also gegeben
durch (![]() ) wenn man die Anfangsbedingungen
) wenn man die Anfangsbedingungen ![]() und
und
![]() als ungerade
Funktionen periodisch auf ganz
als ungerade
Funktionen periodisch auf ganz
![]() fortsetzt.
Eine ungerade periodische Funktion mit Periode 2 L ist auch ungerade
bezüglich der Punkte
fortsetzt.
Eine ungerade periodische Funktion mit Periode 2 L ist auch ungerade
bezüglich der Punkte
![]()
Das bedeutet z.B. für die gezupfte Saite eine Situation wie sie
in Abbildung ![]() dargestellt ist.
dargestellt ist.
Hier können Sie mit der Überlagerung selbst gezeichneter Wellenzüge experimentieren.
Diese Situation legt eine direkte Modellierung der schwingenden Saite durch sich überlagernde Wellenzuüge nahe.