Simulation einer Saite (Karplus-Strong-Algorithmus)

Die vorangegangenen Überlegungen zur Wellengleichung legen es nahe, die schwingende Saite direkt zu modellieren. Die Idee ist einfach:

Abbildung:

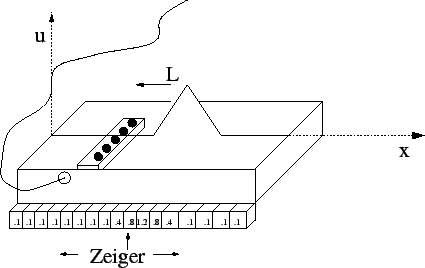
Der Zustand der Saite wird durch einen Vektor von Auslenkungen als Vektor im Computer abgebildet. Er enthält die Wellenformen, zum Beispiel einen Sägezahn oder einen Sinus usw. Der Tonabnehmer registriert die Auslenkung der Saite an einem festen Ort. Dies läßt sich im Computer dadurch simulieren, dass man einen Zeiger, bzw. den Index (ganze Zahl) des Feldes hoch- oder runterzählt. Dadurch ist die Amplitude der Beschleunigung immer gerade der Wert des Feldes an Index- oder Zeigerstellung $i$.

Es ist also, als ob der Tonabnehmer sich an einer fest ausgelegten Saite immer mit der richtigen Geschwindigkeit auf und ab bewegt. Durch die linearität und explizite Lösung der Wellengleichung ist dieses Abtasten einer beliebigen Wellenform eine korrekte Abbildung des Signals am Tonabnehmer. Was noch fehlt ist die Dämpfung.

Die schwingende Saite kommt nach kurzer Zeit zur Ruhe, d.h.$u(x,t)=0$ für $t \rightarrow \infty$ Es gibt drei Dämpfungsmechanismen, die je nach Situation dominant sein können.

1. viskose Dämpfung durch die umgebende Luft
2. innere Dämpfung durch elastischeDehnung und innere Reibung im Saitenmaterial
3. Dämpfung durch Auskoppelung von Schwingungsenergie über die Stege.

Die Unterschiede sind hörbar: z.B.ist bei Metallsaiten die viskose Dämpfung dominant, bei Darm- oder Nylon Saiten die innere Dämpfung. Deshalb klingen Metallsaiten brillanter, Nylonseiten weicher und dumpfer.

Statt die Dämpfung direkt physikalisch zu modellieren, wird sie im Karplus-Strong-Algorithmus durch eine einfache Mittelung ersetzt. Nach dem Auslesen der Amplitude wird $u(i)=(u(i)+u(i-1))/2$ mit $i=1,\dots ,L$ und $i\ne 0$ gesetzt. Damit ist garantiert, dass die Amplitude auf 0 abklingt.

Abbildung: Das Schema des Algorythmus

Die Implementierung sieht dann wie folgt aus:

/*********************************************************************
  zupf.cc -- Modellierung einer gezupften Saite
  Autor    : R. Hilfer
  Zweck    : Beispiel zur Vorlesung, demonstriert Karplus-Strong Alg
  Gebrauch : Eingabe von stdin: 
               frq = Frequenz in Hertz 
               t_max = Gesamtzeit
  Dateien  : Ausgabe auf Datei zupf.raw in binaerem Format
             Umwandlung mit dem Befehl 
               sox -s -w -r 44100 gharmos.raw gharmos.wav
             in wav-Format
  Version  : 1.0 (Originalversion) erstellt am  12.10.2000
 *********************************************************************/

// Einbinden benoetigter Bibliotheken
#include<iostream>
#include<fstream>

int main()
{
// Deklarationen
   double *u;
   double u_0,uprv,t_max,dt,t,frq;
   short amp;
   int plckpt,len,i,iflg,next;

// Parameter abfragen und einlesen
   cout << "Frequenz      :";  cin >> frq;
   cout << "Gesamtdauer   :";  cin >> t_max;

   dt=1./44100.;             // Zeitschritt = Abtastrate
   len = int(44100./frq);    // Laenge der Saite
   plckpt = int(0.1*len);    // Zupfpunkt
   u_0 = 28000;              // Anfangsauslenkung
   t=0.;                     // Zeit initialisieren

// Initialisieren der Saite
   u = new double[len];             // Speicher bereitstellen
   for( i=0; i<=plckpt; i++ ){      // Auffuellen mit Saegezahn
     u[i]=2*u_0*i/plckpt - u_0;
   }
   for( i=len-1; i>plckpt; i-- ){
     u[i]=2*u_0*(len-1-i)/(len-plckpt) - u_0;
   }

// Vorbereitung der binaeren Ausgabedatei
   ofstream outfile("zupf.raw",ios::out|ios::binary); 

   i=0;
   uprv=u[0];
   while(t<t_max){
     u[i] = u[i]*0.5+uprv*0.5;  // Tiefpass = gleitender Mittelwert
     uprv = u[i];               // Tiefpass: Amplitude zwischenspeichern
     amp = short(u[i]);         // Vorbereitung zur Ausgabe in short
     outfile.write(&amp,2);     // binaere Ausgabe : 2 byte schreiben
     t=t+dt;                    // Zeit hochzaehlen
     if(i==len-1) i=-1;         // Zaehler zuruecksetzen
     i++;                       // Index fuer naechste Ausgabe setzen
   }
}

Klicken Sie bitte auf diese Zeile, um den Klang zu hören.

Natürlich ist die Modellierung noch verbesserungsfähig, insbesondere wenn man den Klang einer Gitarre oder ähnlicher Instrumente nachahmen möchte. Es fehlt die gesamte Modellierung des Korpus (Resonator), der Kopplung zwischen Saite und Resonator etc.