



Next: Numerische Lösung
Up: Ein erstes Beispiel: Harmonischer
Previous: Mathematische Umformulierung, Entdimensionalisierung
Wir haben also das Problem
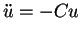 mit Anfangsbedingungen
mit Anfangsbedingungen
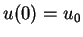 und
und
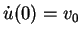 zu lösen.
Dieses Problem ist bekanntlich elementar lösbar und die
Lösung ist eine harmonische Schwingung
zu lösen.
Dieses Problem ist bekanntlich elementar lösbar und die
Lösung ist eine harmonische Schwingung
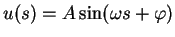 |
(1.14) |
mit Amplitude 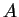 , Phase
, Phase 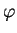 und Frequenz
und Frequenz 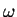 definiert durch
definiert durch
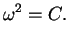 |
(1.15) |
Für 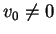 lautet die allgemeine Lösung
dann
lautet die allgemeine Lösung
dann
Im vorliegenden Fall mit 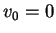 folgt dagegen
folgt dagegen
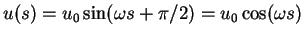 |
(1.16) |
Setzt man die Werte für 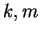 und
und 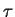 für das
vorliegende Problem ein, so hat
für das
vorliegende Problem ein, so hat 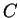 den Wert
den Wert 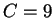 ,
und
,
und 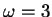 .
Mit
.
Mit 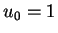 ergibt sich die Lösung des Problems als
ergibt sich die Lösung des Problems als
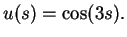 |
(1.17) |
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() und
und ![]() für das
vorliegende Problem ein, so hat
für das
vorliegende Problem ein, so hat ![]() den Wert
den Wert ![]() ,
und
,
und ![]() .
Mit
.
Mit ![]() ergibt sich die Lösung des Problems als
ergibt sich die Lösung des Problems als