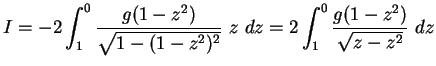Next: Gauß - Quadratur
Up: Integration
Previous: Die Simpsonregel
Mit den bisherigen Integrationsformeln lassen sich auch viele
Problemfälle behandeln, wenn man vorab geschickt umformt.
Beispiel: Man berechne
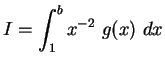 |
(4.21) |
mit
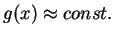 für
für
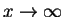 .
Die Anwendung der Simpsonregel bei fester Intervallbreite führt nur zu sehr
langsamer Konvergenz für große
.
Die Anwendung der Simpsonregel bei fester Intervallbreite führt nur zu sehr
langsamer Konvergenz für große 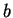 ,
substituiert man jedoch
,
substituiert man jedoch
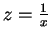 so erhält man mit
so erhält man mit
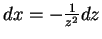
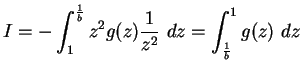 |
(4.22) |
was sich problemlos für große 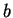 integrieren lässt.
integrieren lässt.
Ähnlich verfährt man bei integrierbaren Singularitäten.
Beispiel: Man berechne
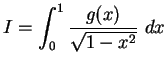 |
(4.23) |
Falls 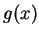 bei
bei 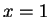 regulär ist, dann hat das Integral bei
regulär ist, dann hat das Integral bei 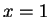 eine integrierbare Singularität. Aber
eine integrierbare Singularität. Aber
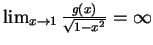 und deshalb lassen sich die
einfachen Integrationsregeln nicht anwenden
und deshalb lassen sich die
einfachen Integrationsregeln nicht anwenden
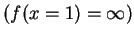 .
.
Die Substitution
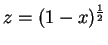 ergibt
ergibt
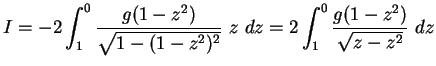 |
(4.24) |
Dies lässt sich dann ohne Probleme integrieren.
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
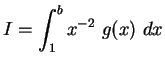
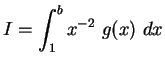
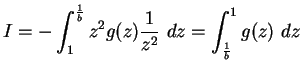
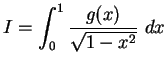
![]() ergibt
ergibt