



Next: Variablen Substitution
Up: Integration
Previous: Die Trapezregel
Nun sei ein gewichteter Funktionsmittelwert gegeben als:
![$\displaystyle \hat{f}_i= \frac{1}{6} \left[f(x_i)+ 4 f \left (\frac{x_i+x_{i-1}}{2} \right ) + f(x_{i-1}) \right] ,$](img284.gif) |
(4.18) |
bzw. die Kurve wird durch eine Parabel angenähert.
Diese ist in Abb. ![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) als gepunktete Linie zu sehen.
als gepunktete Linie zu sehen.
Abbildung:
Schematische Darstellung eines Intervalls, dessen
Fläche nach der Simpsonregel durch eine Parabel approximiert wird.
|
|
Weiterhin kann man zur Vereinfachung konstante Intervallbreiten
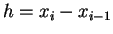 annehmen. Das Integral
annehmen. Das Integral 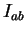 berechnet sich somit zu:
berechnet sich somit zu:
![$\displaystyle I_{ab} = \frac{1}{6} \sum_{i=1}^N (x_i-x_{i-1}) \left[ f(x_i)+ 4f( \bar x_i )+f(x_{i-1})\right] = h \sum_{i=1}^N \hat{f}_i .$](img287.gif) |
(4.19) |
Unter Benutzung der zweiten Ableitung aus Glg. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ):
):
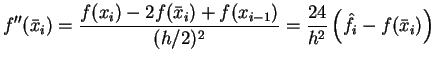 |
(4.20) |
und der Taylorentwicklung von 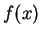 aus Glg. (
aus Glg. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ),
ergibt sich für den Fehler:
),
ergibt sich für den Fehler:
![\begin{eqnarray*}\Delta I_{ab} & = & \sum_{i=1}^N \int_{x_{i-1}}^{x_i} f(x) d...
...
_{\Delta I_{x_{i-1} x_i}} \right ] + h \sum_{i=1}^N \hat{f}_i
\end{eqnarray*}](img289.gif) Daraus folgt der Fehler
Daraus folgt der Fehler
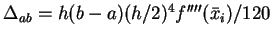 ,
d.h. die Ordnung des Fehlers des Simpson-Verfahrens ist 5.
,
d.h. die Ordnung des Fehlers des Simpson-Verfahrens ist 5.
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![$\displaystyle \hat{f}_i= \frac{1}{6} \left[f(x_i)+ 4 f \left (\frac{x_i+x_{i-1}}{2} \right ) + f(x_{i-1}) \right] ,$](img284.gif)
![$\displaystyle \hat{f}_i= \frac{1}{6} \left[f(x_i)+ 4 f \left (\frac{x_i+x_{i-1}}{2} \right ) + f(x_{i-1}) \right] ,$](img284.gif)
![\includegraphics[width=7cm]{FIGS/simpson.eps}](img285.gif)
![]() annehmen. Das Integral
annehmen. Das Integral ![]() berechnet sich somit zu:
berechnet sich somit zu:
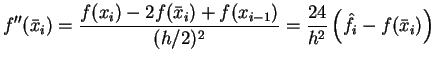
![\begin{eqnarray*}\Delta I_{ab} & = & \sum_{i=1}^N \int_{x_{i-1}}^{x_i} f(x) d...
...
_{\Delta I_{x_{i-1} x_i}} \right ] + h \sum_{i=1}^N \hat{f}_i
\end{eqnarray*}](img289.gif) Daraus folgt der Fehler
Daraus folgt der Fehler