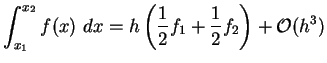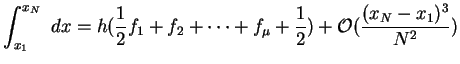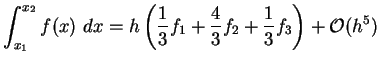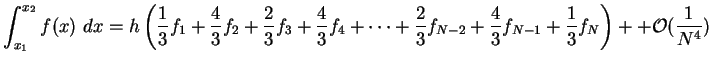Next: Lineare Näherung : L=2
Up: Gauß - Quadratur
Previous: Gauß - Quadratur
In den einfachen Integrationsregeln wird die Funktion 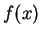 auf dem
Teilintervall
auf dem
Teilintervall
![$ [x_{i-1} , x_{i}]$](img302.gif) verschieden approximiert, und
zwar bei der Mittelpunktsregel durch eine Konstante
verschieden approximiert, und
zwar bei der Mittelpunktsregel durch eine Konstante 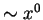 ,
bei der Trapezregel linear
,
bei der Trapezregel linear 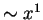 , und bei der
Simpsonregel quadratisch
, und bei der
Simpsonregel quadratisch 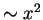 .
.
Das Integrationsintervall
![$ [x_0 , x_n]$](img306.gif) wird in äquidistante
Stützstellen unterteilt, (Intervallbreite
wird in äquidistante
Stützstellen unterteilt, (Intervallbreite 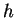 ).
).
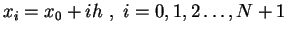 |
(4.25) |
Die Funktionswerte 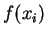 werden abgekürzt als
werden abgekürzt als
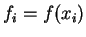 |
(4.26) |
Dann lautet die Trapezregel
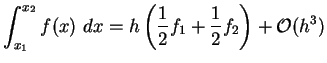 |
(4.27) |
oder durch Zusammensetzen von 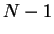 Intervallen
Intervallen
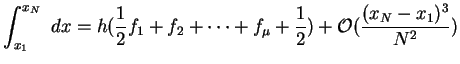 |
(4.28) |
oder die Simpson-Regel
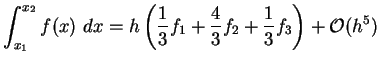 |
(4.29) |
oder für die Zusammensetzung von 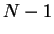 Intervallen
Intervallen
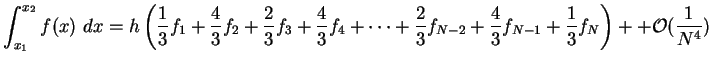 |
(4.30) |
Die allgemeine Struktur ist also stets von der Art
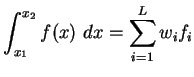 |
(4.31) |
mit 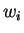 (z.B.
(z.B.
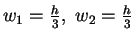 für die
Simpsonregel)
Wir wollen diese zwei Regeln für
für die
Simpsonregel)
Wir wollen diese zwei Regeln für 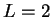 und
und 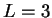 noch einmal
herleiten, um dann zu verallgemeinern.
noch einmal
herleiten, um dann zu verallgemeinern.




Next: Lineare Näherung : L=2
Up: Gauß - Quadratur
Previous: Gauß - Quadratur
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() wird in äquidistante
Stützstellen unterteilt, (Intervallbreite
wird in äquidistante
Stützstellen unterteilt, (Intervallbreite ![]() ).
).
![]() werden abgekürzt als
werden abgekürzt als