3 Discussion

3.1 (Non-)locality and (in-)finite propagation speed

[335.4.1] It is the primary objective of this note to contribute to the current debate by discussing fundamental differences between the cases $\alpha=2$ and $0<\alpha<2$ in eq. (1) for applications to experiment. [335.4.2] The decisive difference between the cases $\alpha=2$ and $0<\alpha<2$ is the locality of the Laplacean $-\Delta$ for $\alpha=2$ in contrast with the nonlocality of the fractional Laplacean $(-\Delta)^{{\alpha/2}}$ for $0<\alpha<2$ .

[page 336, §1] [336.2.1] Before discussing the (non-)locality of $(-\Delta)^{{\alpha/2}}$ it seems important to distinguish it from another nonlocality appearing in eq. (1). [336.2.2] It is sometimes argued that also the case $\alpha=2$ shows nonlocality in the sense that a localized initial condition such as $u(x,0)=h(x)=\delta(x-x_{0})$ , vanishing everywhere except at $x_{0}$ for $t=0$ , spreads out instantaneously to all $x$ such that $u(x,t)\neq 0$ for all $x$ for $t>0$ . [336.2.3] This initially infinite “speed of propagation” violates relativistic locality. While this is true for all $0<\alpha\leq 2$ , it concerns the operator $\partial/\partial t+(-\Delta)^{{\alpha/2}}$ and occurs only at $t=0$ , the initial instant. [336.2.4] For $\alpha=2$ the operator $\Delta$ is local and also $\partial/\partial t+(-\Delta)$ is perfectly local for all $t>0$ . [336.2.5] While an infinite propagation speed occurs also for $0<\alpha<2$ another violation of locality occurs in this case. [336.2.6] This has more dramatic implications for experiment, as will now be discussed.

3.2 Probabilistic interpretation

[336.3.1] The fundamental difference between the cases $\alpha=2$ and $0<\alpha<2$ can be understood from the deep and well known relation between the diffusion equation (1) and the theory of stochastic processses. [336.3.2] The probabilistic interpretation of $u(x)$ is given in terms of families of stochastic processes $(X_{t})_{{t\geq 0}}$ indexed by their starting point $X_{0}=x\in\mathbb{B}(z,R)$ through the formula

$u(x)=\langle u(X_{{T^{e}(\mathbb{R}^{d}\setminus\mathbb{B}(z,R)}})\rangle _{x},$

(5)

where $T^{e}(\mathbb{R}^{d}\setminus\mathbb{B}(z,R)$ denotes the first exit time of a path starting at $X_{0}=x\in\mathbb{B}(z,R)$ and hitting the set $\mathbb{R}^{d}\setminus\mathbb{B}(z,R)$ for the first time at $t=T^{e}(\mathbb{R}^{d}\setminus\mathbb{B}(z,R)$ . [336.3.3] The brackets $\langle Y\rangle _{x}$ denote the expectation value of a random variable $Y$ evaluated for the process $(X_{t})_{{t\geq 0}}$ starting from $x$ at $t=0$ .

[336.4.1] For $\alpha=2$ the family of stochastic processes has almost surely continuous paths. [336.4.2] Because of this, a path starting from $x\in\mathbb{B}(z,R)$ at $t=0$ will exit from $\mathbb{B}(z,R)$ when hitting $\partial\mathbb{B}(z,R)=\{ x\in\mathbb{R}^{d}:|x-z|=R\}$ for the first time.

[336.5.1] For $0<\alpha<2$ on the other hand the families of stochastic processes have almost surely discontinuous paths that can jump over the boundary $\partial\mathbb{B}(z,R)$ . [336.5.2] As a result the first exit occurs not at the boundary but at some point $X_{{T^{e}(\mathbb{R}^{d}\setminus\mathbb{B}(z,R))}}$ deep in the exterior region $\mathbb{R}^{d}\setminus\mathbb{B}(z,R)$ .

[336.6.1] In applications to particle diffusion the unknown $u(x,t)$ is often the concentration of atomic, molecular or tracer particles and fractional generalizations of Ficks law have been postulated [4, 27, 3]. [336.6.2] Note, however, that the probabilistic interpretation is frequently not physical even for $\alpha=2$ . [336.6.3] There are at least two possible reasons: [336.6.4] Firstly, the underlying physical dynamics may not be stochastic. [336.6.5] Secondly, fundamental laws of probability [page 337, §0] theory may be violated as for the case of heat diffusion where $u(x,t)$ is the temperature field. [337.0.1] In such cases the random “paths” are fictitious as are the “particles” and their “trajectories” in the sense that they cannot be observed directly in an experiment.

[337.1.1] Whether or not a probabilistic interpretation applies, the discontinuity of the trajectories in the probabilistic interpretation leads to experimental difficulties. [337.1.2] This can be seen from considering the stationary states of (1),(2) and (4).

3.3 Stationary solutions

[337.2.1] To explore the physical consequences of the initial and boundary value problem (1),(2) and (4) it is useful to start with stationary solutions, i.e. solutions of the form

$u(x,t)=u(x).$

(6)

[337.2.2] The fractional diffusion equation then reduces to the fractional Riesz-Dirichlet problem

	$\displaystyle(-\Delta)^{{\alpha/2}}u(x)=0,\qquad x\in\mathbb{B}$		(7a)
	$\displaystyle u(x)=g(x),\qquad x\in\mathbb{R}^{d}\setminus\mathbb{B}$		(7b)

for suitable boundary data $g(x)$ such that

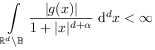$\int\limits _{{\mathbb{R}^{d}\setminus\mathbb{B}}}\frac{|g(x)|}{1+|x|^{{d+\alpha}}}\;\mathrm{d}^{d}x<\infty$

(8)

holds.

[337.3.1] The solution of the fractional Riesz-Dirichlet problem for the case of a sphere $\mathbb{B}=\mathbb{B}(z,R)=\{ x\in\mathbb{R}^{d}:|x-z|<R\}$ of radius $R$ centered at $z\in\mathbb{R}^{d}$ is the fractional Poisson integral [16]

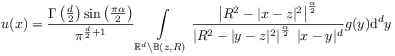$u(x)=\frac{\Gamma\left(\frac{d}{2}\right)\sin\left(\frac{\pi\alpha}{2}\right)}{\pi^{{\frac{d}{2}+1}}}\int\limits _{{\mathbb{R}^{d}\setminus\mathbb{B}(z,R)}}\frac{\left|R^{2}-|x-z|^{2}\right|^{{\frac{\alpha}{2}}}}{\left|R^{2}-|y-z|^{2}\right|^{{\frac{\alpha}{2}}}\;|x-y|^{d}}g(y)\mathrm{d}^{d}y$

(9)

for $x\in\mathbb{B}(z,R)$ . [337.3.2] For $\alpha\to 2$ the solution reduces to the conventional Poisson integral

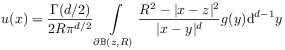$u(x)=\frac{\Gamma(d/2)}{2R\pi^{{d/2}}}\int\limits _{{\partial\mathbb{B}(z,R)}}\frac{R^{2}-|x-z|^{2}}{|x-y|^{d}}g(y)\mathrm{d}^{{d-1}}y$

(10)

for $x\in\mathbb{B}(z,R)$ and $u(x)=g(x)$ for $x\in\partial\mathbb{B}(z,R)$ .

[337.4.1] Although the fractional Poisson formula eq. (9) has been known for nearly 70 years [22] its crucial difference to (10) seems to have escaped the attention of those scientists, who propose eq. (1) or its variants as a mathematical model for physical phenomena. [337.4.2] Perhaps this is due to [page 338, §0] the fact that many workers assume explicitly or implicitly “absorbing” or “killing” boundaries $g=0$ for all $x\in\mathbb{R}^{d}\setminus\mathbb{B}(z,R)$ . [338.0.1] Physically this means that there are no atoms, molecules or tracer particles outside the spherical container $\mathbb{B}(z,R)$ . [338.0.2] Any particle that jumps out of $\mathbb{B}(z,R)$ is considered to be instantaneously removed from the experiment. [338.0.3] The environment surrounding the experimental apparatus has to be kept absolutely clean at all times for these boundary conditions to apply. [338.0.4] Under these experimental conditions both equations, eq. (9) as well as eq. (10), agree and both predict

$u(x)=0$

(11)

for all $x\in\mathbb{R}^{d}$ and all $0<\alpha\leq 2$ .

[338.1.1] Consider next the case when there exist regions where the atomic, molecular or tracer particles are not instantaneously removed. [338.1.2] For simplicity let there exist several small nonoverlapping spherical containers $\mathbb{B}(z_{i},R_{i})$ with $i=1,...,n$ , $\mathbb{B}(z_{i},R_{i})\cap\mathbb{B}(z_{j},R_{j})=\emptyset$ for all $i\neq j$ and $\mathbb{B}(z_{i},R_{i})\cap\mathbb{B}(z,R)=\emptyset$ for all $i$ in which particles are kept (e.g. for replenishment). [338.1.3] This means that in these containers $g(x)\neq 0$ and particles jumping out of the sample region $\mathbb{B}(z,R)$ may land in one of these containers. [338.1.4] They are not removed until the container is filled and a maximum concentration is reached. [338.1.5] Let $u_{i}\in\mathbb{R}$ denote the maximal concentration in each container. [338.1.6] Assume that

$g(x)=\sum _{{i=1}}^{n}R_{i}^{{-d}}\phi _{i}\left(\frac{x-z_{i}}{R_{i}}\right)$		(12a)
with
$\phi _{i}(x)=\begin{cases}u_{i}\exp\left(-\frac{1}{1-\|x\|^{2}}\right)&\mathrm{for~}x\in\mathbb{B}(0,1)\\ 0&\mathrm{otherwise}\end{cases}$		(12b)

describes the concentration field in the region $\mathbb{R}\setminus\mathbb{B}(z,R)$ outside the sample. [338.1.7] Other functions than $\phi _{i}(x)$ with $supp\phi _{i}\subset\mathbb{B}(z_{j},R_{j})$ are possible. [338.1.8] Assume also that $R_{i}\ll R$ for all $i$ , so that in particular also supp $g\cap\partial\mathbb{B}(z,R)=\emptyset$ holds.

[338.2.1] For $\alpha=2$ eq. (10) shows that the solution $u(x)=0$ remains unaffected by the containers $\mathbb{B}(z_{i},R_{i})$ and their content. [338.2.2] For $0<\alpha<2$ on the other hand the solution changes and becomes nonzero. It is approximately

$u(x)\approx\frac{\Gamma\left(\frac{d}{2}\right)\sin\left(\frac{\pi\alpha}{2}\right)}{\pi^{{\frac{d}{2}+1}}}\sum _{{i=1}}^{n}\frac{u_{i}\left|R^{2}-|x-z|^{2}\right|^{{\frac{\alpha}{2}}}}{\left|R^{2}-|z_{i}-z|^{2}\right|^{{\frac{\alpha}{2}}}\;|x-z_{i}|^{d}}\neq 0$

(13)

for $x\in\mathbb{B}(z,R)$ . [338.2.3] This result implies that for $0<\alpha<2$ the stationary solution inside the sample region $\mathbb{B}(z,R)$ depends on the location and content of all other containers $\mathbb{B}(z_{i},R_{i})$ in the laboratory. [338.2.4] The sample in $\mathbb{B}(z,R)$ [page 339, §0] cannot be shielded or isolated from other samples in the laboratory. [339.0.1] It should be easy to verify or falsify this prediction in an experiment.

Authors:	R. Hilfer
originally published in:	???
originally submitted:	???