3 Geometric Characterizations

3.1 General Considerations

[206.2.3] A general geometric characterization of stochastic media should provide macroscopic geometric observables that allow to distinguish media with different microstructures quantitatively. [206.2.4] In general, a stochastic medium is defined as a probability distribution on a space of geometries or configurations. [206.2.5] Distributions and expectation values of geometric observables are candidates for a general geometric characterization.

[206.3.1] A general geometric characterization should fulfill four criteria to be useful in applications. [206.3.2] These four criteria were advanced in [30]. [206.3.3] First, it must be well defined. [206.3.4] This obvious requirement is sometimes violated. [206.3.5] The so called ‘‘pore size distributions’’ measured in mercury porosimetry are not geometrical observables in the sense that they cannot be determined from knowledge of the geometry alone. [206.3.6] Instead they are capillary pressure curves whose calculation involves physical quantities such as surface tension, viscosity or flooding history [30]. [206.3.7] Second, the geometric characterization should be directly accessible in experiments. [206.3.8] The experiments should be independent of the quantities to be predicted. [206.3.9] Thirdly, the numerical implementation should not require excessive amounts of data. [206.3.10] This means that the amount of data should be manageable by contemporary data processing technology. [206.3.11] Finally, a useful geometric characterization should be helpful in the exact or approximate theoretical calculations.

[206.4.1] For simplicity only two-component media will be considered throughout this paper, but most concepts can be generalized to media with an arbitrary finite number of components.

3.2 Geometric Observables

[206.4.2] Well defined geometric observables are the basis for the geometric characterization of porous media. [206.4.3] A perennial problem in all applications is to identify those [page 207, §0] macroscopic geometric observables that are relevant for distinguishing between classes of microstructures. [207.0.1] One is interested in those properties of the microstructure that influence the macroscopic physical behaviour. [207.0.2] In general this depends on the details of the physical problem, but some general properties of the microstructure such as volume fraction or porosity are known to be relevant in many situations. [207.0.3] Hadwigers theorem [23] is an example of a mathematical result that helps to identify an important class of such general geometric properties of porous media. [207.0.4] It will be seen later, however, that there exist important geometric properties that are not members of this class.

[207.1.1] A two component porous (or heterogenous) sample $\mathbb{S}\subset\mathbb{R}^{d}$ consists of two closed subsets $\mathbb{P}\subset\mathbb{R}^{d}$ and $\mathbb{M}\subset\mathbb{R}^{d}$ called pore space $\mathbb{P}$ and matrix $\mathbb{M}$ such that $\mathbb{S}=\mathbb{P}\cup\mathbb{M}$ . [207.1.2] Its internal boundary is denoted as $\partial\mathbb{P}=\partial\mathbb{M}=\mathbb{P}\cap\mathbb{M}$ [207.1.3] The boundary $\partial\mathbb{G}$ of a set is defined as the difference between the closure and the interior of $\mathbb{G}$ where the closure is the intersection of all closed sets containing $\mathbb{G}$ and the interior is the union of all open sets contained in $\mathbb{G}$ . [207.1.4] A geometric observable $f$ is a mapping (functional) that assigns to each admissible $\mathbb{P}$ a real number $f(\mathbb{P})=f(\mathbb{P}\cap\mathbb{S})$ that can be calculated from $\mathbb{P}$ without solving a physical boundary value problem. [207.1.5] A functional whose evaluation requires the solution of a physical boundary value problem will be called a physical observable.

[207.2.1] Before discussing examples for geometric observables it is necessary to specify the admissible geometries $\mathbb{P}$ . [207.2.2] The set ${\mathcal{R}}$ of admissible $\mathbb{P}$ is defined as the set of all finite unions of compact convex sets [23, 61, 58, 57, 44](see also the papers by M. Kerscher and K. Mecke in this volume). [207.2.3] Because ${\mathcal{R}}$ is closed under unions and intersections it is called the convex ring. [207.2.4] The choice of ${\mathcal{R}}$ is convenient for applications because digitized porous media can be considered as elements from ${\mathcal{R}}$ and because continuous observables defined for convex compact sets can be continued to all of ${\mathcal{R}}$ . [207.2.5] The set of all compact and convex subsets of $\mathbb{R}^{d}$ is denoted as ${\mathcal{K}}$ . [207.2.6] For subsequent discussions the Minkowski addition of two sets $\mathbb{A},\mathbb{B}\subset\mathbb{R}^{d}$ is defined as

$\mathbb{A}+\mathbb{B}=\{\boldsymbol{x}+\boldsymbol{y}:\boldsymbol{x}\in\mathbb{A},\boldsymbol{y}\in\mathbb{B}\}.$

(8)

[207.2.7] Multiplication of $\mathbb{A}$ with a scalar is defined by $a\mathbb{A}=\{ a\boldsymbol{x}:x\in\mathbb{A}\}$ for $a\in\mathbb{R}$ .

[207.3.1] Examples of geometric observables are the volume of $\mathbb{P}$ or the surface area of its boundary $\partial\mathbb{P}$ . [207.3.2] Let

$V_{d}(\mathbb{K})=\int _{{\mathbb{R}^{d}}}\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}})\mbox{\rm d}^{d}{\boldsymbol{r}}$

(9)

denote the $d$ -dimensional Lebesgue volume of the compact convex set $\mathbb{K}$ . [207.3.3] The volume is hence a functional $V_{d}:{\mathcal{K}}\to\mathbb{R}$ on ${\mathcal{K}}$ . [207.3.4] An example of a compact convex set is the unit ball $\mathbb{B}^{d}=\{\boldsymbol{x}\in\mathbb{R}^{d}:|\boldsymbol{x}|\leq 1\}=\mathbb{B}^{d}(\boldsymbol{0},1)$ centered at the origin $\boldsymbol{0}$ whose volume is

$\kappa _{d}=V_{d}(\mathbb{B}^{d})=\frac{\pi^{{d/2}}}{\Gamma(1+(d/2))}.$

(10)

[207.3.5] Other functionals on ${\mathcal{K}}$ can be constructed from the volume by virtue of the following fact. [207.3.6] For every compact convex $\mathbb{K}\in{\mathcal{K}}$ and every $\varepsilon\geq 0$ there are [page 208, §0] numbers $V_{j}(\mathbb{K}),j=0,\ldots,d$ depending only on $\mathbb{K}$ such that

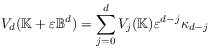$V_{d}(\mathbb{K}+\varepsilon\mathbb{B}^{d})=\sum _{{j=0}}^{d}V_{j}(\mathbb{K})\varepsilon^{{d-j}}\kappa _{{d-j}}$

(11)

is a polynomial in $\varepsilon$ . [208.0.1] This result is known as Steiners formula [23, 61]. [208.0.2] The numbers $V_{j}(\mathbb{K}),j=0\ldots,d$ define functionals on ${\mathcal{K}}$ similar to the volume $V_{d}(\mathbb{K})$ . [208.0.3] The quantities

$W_{i}(\mathbb{K})=\frac{\kappa _{i}V_{{d-i}}(\mathbb{K})}{\binom{d}{i}}$

(12)

are called quermassintegrals [57]. [208.0.4] From (11) one sees that

$\lim _{{\varepsilon\to 0}}\frac{1}{\varepsilon}(V_{d}(\mathbb{K}+\varepsilon\mathbb{B}^{d})-V_{d}(\mathbb{K}))=\kappa _{1}V_{{d-1}}(\mathbb{K}),$

(13)

and from (10) that $\kappa _{1}=2$ . [208.0.5] Hence $V_{{d-1}}(\mathbb{K})$ may be viewed as half the surface area. [208.0.6] The functional $V_{1}(\mathbb{K})$ is related to the mean width $w(\mathbb{K})$ defined as the mean value of the distance between a pair of parallel support planes of $\mathbb{K}$ . [208.0.7] The relation is

$V_{1}(\mathbb{K})=\frac{d\kappa _{d}}{2\kappa _{{d-1}}}w(\mathbb{K})$

(14)

which reduces to $V_{1}(\mathbb{K})=w(\mathbb{K})/2$ for $d=3$ . [208.0.8] Finally the functional $V_{0}(\mathbb{K})$ is evaluated from (11) by dividing with $\varepsilon^{d}$ and taking the limit $\varepsilon\rightarrow\infty$ . [208.0.9] It follows that $V_{0}(\mathbb{K})=1$ for all $\mathbb{K}\in{\mathcal{K}}\setminus\{\emptyset\}$ . [208.0.10] One extends $V_{0}$ to all of ${\mathcal{K}}$ by defining $V_{0}(\emptyset)=0$ . [208.0.11] The geometric observable $V_{0}$ is called Euler characteristic.

[208.1.1] The geometric observables $V_{i}$ have several important properties. [208.1.2] They are Euclidean invariant (i.e. invariant under rigid motions), additive and monotone. [208.1.3] Let $T_{d}\cong(\mathbb{R}^{d},+)$ denote the group of translations with vector addition as group operation and let $SO(d)$ be the matrix group of rotations in $d$ dimensions [5]. [208.1.4] The semidirect product $E_{d}=T_{d}\odot SO(d)$ is the Euclidean group of rigid motions in $\mathbb{R}^{d}$ . [208.1.5] It is defined as the set of pairs $(\boldsymbol{a},A)$ with $\boldsymbol{a}\in\mbox{\rm T}_{d}$ and $A\in SO(d)$ and group operation

$(\boldsymbol{a},A)\circ(\boldsymbol{b},B)=(\boldsymbol{a}+A\boldsymbol{b},AB).$

(15)

[208.1.6] An observable $f:{\mathcal{K}}\to\mathbb{R}$ is called euclidean invariant or invariant under rigid motions if

$f(\boldsymbol{a}+A\mathbb{K})=f(\mathbb{K})$

(16)

holds for all $(\boldsymbol{a},A)\in E_{d}$ and all $\mathbb{K}\in{\mathcal{K}}$ . [208.1.7] Here $A\mathbb{K}=\{ A\boldsymbol{x}:\boldsymbol{x}\in\mathbb{K}\}$ denotes the rotation of $\mathbb{K}$ and $\boldsymbol{a}+\mathbb{K}=\{\boldsymbol{a}\}+\mathbb{K}$ its translation. [208.1.8] A geometric observable $f$ is called additive if

$\displaystyle f(\emptyset)$	$\displaystyle=0$		(17a)
$\displaystyle f(\mathbb{K}_{1}\cup\mathbb{K}_{2})+f(\mathbb{K}_{1}\cap\mathbb{K}_{2})$	$\displaystyle=f(\mathbb{K}_{1})+f(\mathbb{K}_{2})$		(17b)

holds for all $\mathbb{K}_{1},\mathbb{K}_{2}\in{\mathcal{K}}$ with $\mathbb{K}_{1}\cup\mathbb{K}_{2}\in{\mathcal{K}}$ . [208.1.9] Finally a functional is called monotone if for $\mathbb{K}_{1},\mathbb{K}_{2}\in{\mathcal{K}}$ with $\mathbb{K}_{1}\subset\mathbb{K}_{2}$ follows $f(\mathbb{K}_{1})\leq f(\mathbb{K}_{2})$ .

[page 209, §1] [209.1.1] The special importance of the functionals $V_{i}(\mathbb{K})$ arises from the following theorem of Hadwiger [23]. [209.1.2] A functional $f:{\mathcal{K}}\to\mathbb{R}$ is euclidean invariant, additive and monotone if and only if it is a linear combination

$f=\sum _{{i=0}}^{d}c_{i}V_{i}$

(18)

with nonnegative constants $c_{0},\ldots,c_{d}$ . [209.1.3] The condition of monotonicity can be replaced with continuity and the theorem remains valid [23]. [209.1.4] If $f$ is continuous on ${\mathcal{K}}$ , additive and euclidean invariant it can be additively extended to the convex ring ${\mathcal{R}}$ [58]. [209.1.5] The additive extension is unique and given by the inclusion-exclusion formula

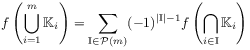$f\left(\bigcup _{{i=1}}^{m}\mathbb{K}_{i}\right)=\sum _{{\mathbb{I}\in{\mathcal{P}}(m)}}(-1)^{{|\mathbb{I}|-1}}f\left(\bigcap _{{i\in\mathbb{I}}}\mathbb{K}_{i}\right)$

(19)

where ${\mathcal{P}}(m)$ denotes the family of nonempty subsets of $\{ 1,\ldots,m\}$ and $|\mathbb{I}|$ is the number of elements of $\mathbb{I}\in{\mathcal{P}}(m)$ . [209.1.6] In particular, the functionals $V_{i}$ have a unique additive extension to the convex ring ${\mathcal{R}}$ [58], which is again be denoted by $V_{i}$ .

[209.2.1] For a threedimensional porous sample with $\mathbb{P}\in{\mathcal{R}}$ the extended functionals $V_{i}$ lead to two frequently used geometric observables. [209.2.2] The first is the porosity of a porous sample $\mathbb{S}$ defined as

$\phi(\mathbb{P}\cap\mathbb{S})=\phi _{3}(\mathbb{P}\cap\mathbb{S})=\frac{V_{3}(\mathbb{P}\cap\mathbb{S})}{V_{3}(\mathbb{S})},$

(20)

and the second its specific internal surface area which may be defined in view of (13) as

$\phi _{2}(\mathbb{P}\cap\mathbb{S})=\frac{2V_{2}(\mathbb{P}\cap\mathbb{S})}{V_{3}(\mathbb{S})}.$

(21)

[209.2.3] The two remaining observables $\phi _{1}(\mathbb{P})=V_{1}(\mathbb{P}\cap\mathbb{S})/V_{3}(\mathbb{S})$ and $\phi _{0}(\mathbb{P})=V_{0}(\mathbb{P}\cap\mathbb{S})/V_{3}(\mathbb{S})$ have received less attention in the porous media literature. [209.2.4] The Euler characteristic $V_{0}$ on ${\mathcal{R}}$ coincides with the identically named topological invariant. [209.2.5] For $d=2$ and $\mathbb{G}\in{\mathcal{R}}$ one has $V_{0}(\mathbb{G})=c(\mathbb{G})-c^{{\prime}}(\mathbb{G})$ where $c(\mathbb{G})$ is the number of connectedness components of $\mathbb{G}$ , and $c^{{\prime}}(\mathbb{G})$ denotes the number of holes (i.e. bounded connectedness components of the complement).

3.3 Definition of Stochastic Porous Media

[209.2.6] For theoretical purposes the pore space $\mathbb{P}$ is frequently viewed as a random set [61, 30]. [209.2.7] In practical applications the pore space is usually discretized because of measurement limitations and finite resolution. [209.2.8] For the data discussed below the set $\mathbb{S}\subset\mathbb{R}^{3}$ is a rectangular parallelepiped whose sidelengths are $M_{1},M_{2}$ and $M_{3}$ in units of the lattice constant $a$ (resolution) of a simple cubic lattice. [209.2.9] The position vectors ${\boldsymbol{r}}_{i}={\boldsymbol{r}}_{{i_{1}\ldots i_{d}}}=(ai_{1},\ldots,ai_{d})$ with integers $1\leq i_{j}\leq M_{j}$ are

[page 210, §0] used to label the lattice points, and ${\boldsymbol{r}}_{i}$ is a shorthand notation for ${\boldsymbol{r}}_{{i_{1}\ldots i_{d}}}$ . [210.0.1] Let $\mathbb{V}_{i}$ denote a cubic volume element (voxel) centered at the lattice site ${\boldsymbol{r}}_{i}$ . [210.0.2] Then the discretized sample may be represented as $\mathbb{S}=\bigcup _{{i=1}}^{N}\mathbb{V}_{i}$ . [210.0.3] The discretized pore space $\widetilde{\mathbb{P}}$ defined as

$\widetilde{\mathbb{P}}=\bigcup _{{\{ i:\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{i})=1\}}}\mathbb{V}_{i}$

(22)

is an approximation to the true pore space $\mathbb{P}$ . [210.0.4] For simplicity it will be assumed that the discretization does not introduce errors, i.e. that $\widetilde{\mathbb{P}}=\mathbb{P}$ , and that each voxel is either fully pore or fully matrix. [210.0.5] This assumption may be relaxed to allow voxel attributes such as internal surface or other quermassintegral densities. [210.0.6] The discretization into voxels reflects the limitations arising from the experimental resolution of the porous structure. [210.0.7] A discretized pore space for a bounded sample belongs to the convex ring ${\mathcal{R}}$ if the voxels are convex and compact. [210.0.8] Hence, for a simple cubic discretization the pore space belongs to the convex ring. [210.0.9] A configuration (or microstructure) ${\boldsymbol{Z}}$ of a $2$ -component medium may then be represented in the simplest case by a sequence

${\boldsymbol{Z}}=(Z_{1},\ldots,Z_{N})=(\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{1}),\ldots,\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{N}))$

(23)

where ${\boldsymbol{r}}_{i}$ runs through the lattice points and $N=M_{1}M_{2}M_{3}$ . [210.0.10] This representation corresponds to the simplest discretization in which there are only two states for each voxel indicating whether it belongs to pore space or not. [210.0.11] In general a voxel could be characterized by more states reflecting the microsctructure within the region $\mathbb{V}_{i}$ . [210.0.12] In the simplest case there is a one-to-one correspondence between $\mathbb{P}$ and ${\boldsymbol{Z}}$ given by (23). [210.0.13] Geometric observables $f(\mathbb{P})$ then correspond to functions $f({\boldsymbol{Z}})=f(z_{1},\ldots,z_{N})$ .

[210.1.1] As a convenient theoretical idealization it is frequently assumed that porous media are random realizations drawn from an underlying statistical ensemble. [210.1.2] A discretized stochastic porous medium is defined through the discrete probability density

$p(z_{1},\ldots,z_{N})=\mbox{Prob}\{(Z_{1}=z_{1})\wedge\ldots\wedge(Z_{N}=z_{N})\}$

(24)

where $z_{i}\in\{ 0,1\}$ in the simplest case. [210.1.3] It should be emphasized that the probability density $p$ is mainly of theoretical interest. [210.1.4] In practice it is usually not known. [210.1.5] An infinitely extended medium or microstructure is called stationary or statistically homogeneous if $p$ is invariant under spatial translations. [210.1.6] It is called isotropic if $p$ is invariant under rotations.

3.4 Moment Functions and Correlation Functions

[210.1.7] A stochastic medium was defined through its probability distribution $p$ . [210.1.8] In practice $p$ will be even less accessible than the microstructure $\mathbb{P}={\boldsymbol{Z}}$ itself. [210.1.9] Partial information about $p$ can be obtained by measuring or calculating expectation values of a geometric observable $f$ . [210.1.10] These are defined as

$\langle f(z_{1},\ldots,z_{N})\rangle=\sum _{{z_{1}=0}}^{1}\ldots\sum _{{z_{N}=0}}^{1}f(z_{1},\ldots,z_{N})p(z_{1},\ldots,z_{N})$

(25)

[page 211, §0] where the summations indicate a summation over all configurations. [211.0.1] Consider for example the porosity $\phi(\mathbb{S})$ defined in (20). [211.0.2] For a stochastic medium $\phi(\mathbb{S})$ becomes a random variable. [211.0.3] Its expectation is

$\displaystyle\left\langle\phi\right\rangle$	$\displaystyle=\frac{\left\langle V_{3}(\mathbb{P})\right\rangle}{V_{3}(\mathbb{S})}=\frac{1}{V_{3}(\mathbb{S})}\int _{{\mathbb{S}}}\left\langle\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}})\right\rangle\mbox{\rm d}^{3}{\boldsymbol{r}}$
	$\displaystyle=\frac{1}{V_{3}(\mathbb{S})}\sum _{{i=1}}^{N}\left\langle z_{i}\right\rangle V_{3}(\mathbb{V}_{i})=\frac{1}{N}\sum _{{i=1}}^{N}\left\langle z_{i}\right\rangle$
	$\displaystyle=\frac{1}{N}\sum _{{i=1}}^{N}\mbox{Prob}\{ z_{i}=1\}=\frac{1}{N}\sum _{{i=1}}^{N}\mbox{Prob}\{{\boldsymbol{r}}_{i}\in\mathbb{P}\}$	(26)

If the medium is statistically homogeneous then

$\left\langle\phi\right\rangle=\mbox{Prob}\{ z_{i}=1\}=\mbox{Prob}\{{\boldsymbol{r}}_{i}\in\mathbb{P}\}=\left\langle\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{i})\right\rangle$

(27)

independent of $i$ . [211.0.4] It happens frequently that one is given only a single sample, not an ensemble of samples. [211.0.5] It is then necessary to invoke an ergodic hypothesis that allows to equate spatial averages with ensemble averages.

[211.1.1] The porosity is the first member in a hierarchy of moment functions. [211.1.2] The $n$ -th order moment function is defined generally as

$S_{n}({\boldsymbol{r}}_{1},\ldots,{\boldsymbol{r}}_{n})=\left\langle\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{1})\ldots\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{n})\right\rangle$

(28)

for $n\leq N$ . ^b (This is a footnote:) ^b If a voxel has other attributes besides being pore or matrix one may define also mixed moment functions $S_{{i_{1}\ldots i_{n}}}({\boldsymbol{r}}_{1},\ldots,{\boldsymbol{r}}_{n})=\left\langle\phi _{{i_{1}}}({\boldsymbol{r}}_{1})\ldots\phi _{{i_{n}}}({\boldsymbol{r}}_{n})\right\rangle$ where $\phi _{i}({\boldsymbol{r}}_{j})=V_{i}(\mathbb{P}\cap\mathbb{V}_{j})/V_{i}(\mathbb{V}_{j})$ for $i=1,\ldots d$ are the quermassintegral densities for the voxel at site ${\boldsymbol{r}}_{j}$ . [211.1.3] For stationary media $S_{n}({\boldsymbol{r}}_{1},\ldots{\boldsymbol{r}}_{n})=g({\boldsymbol{r}}_{1}-{\boldsymbol{r}}_{n},\ldots,{\boldsymbol{r}}_{{n-1}}-{\boldsymbol{r}}_{n})$ where the function $g$ depends only on $n-1$ variables. [211.1.4] Another frequently used expectation value is the correlation function which is related to $S_{2}$ . [211.1.5] For a homogeneous medium it is defined as

$G({\boldsymbol{r}}_{0},{\boldsymbol{r}})=G({\boldsymbol{r}}-{\boldsymbol{r}}_{0})=\frac{\left\langle\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{0})\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}})\right\rangle-\left\langle\phi\right\rangle^{2}}{\left\langle\phi\right\rangle(1-\left\langle\phi\right\rangle)}=\frac{S_{2}({\boldsymbol{r}}-{\boldsymbol{r}}_{0})-(S_{1}({\boldsymbol{r}}_{0}))^{2}}{S_{1}({\boldsymbol{r}}_{0})(1-S_{1}({\boldsymbol{r}}_{0}))}$

(29)

where ${\boldsymbol{r}}_{0}$ is an arbitrary reference point, and $\left\langle\phi\right\rangle=S_{1}({\boldsymbol{r}}_{0})$ . [211.1.6] If the medium is isotropic then $G({\boldsymbol{r}})=G(|{\boldsymbol{r}}|)=G(r)$ . [211.1.7] Note that $G$ is normalized such that $G(0)=1$ and $G(\infty)=0$ .

[211.2.1] The hierarchy of moment functions $S_{n}$ , similar to $p$ , is mainly of theoretical interest. [211.2.2] For a homogeneous medium $S_{n}$ is a function of $n-1$ variables. [211.2.3] To specify $S_{n}$ numerically becomes impractical as $n$ increases. [211.2.4] If only $100$ points are required along each coordinate axis then giving $S_{n}$ would require $10^{{2d(n-1)}}$ numbers. [211.2.5] For $d=3$ this implies that already at $n=3$ it becomes economical to specify the microstructure $\mathbb{P}$ directly rather than incompletely through moment or correlation functions.

[page 212, §1]

3.5 Contact Distributions

[212.1.1] An interesting geometric characteristic introduced and discussed in the field of stochastic geometry are contact distributions [18, 61, p. 206]. [212.1.2] Certain special cases of contact distributions have appeared also in the porous media literature [20]. [212.1.3] Let $\mathbb{G}$ be a compact test set containing the origin $\boldsymbol{0}$ . [212.1.4] Then the contact distribution is defined as the conditional probability

$H_{\mathbb{G}}(r)=1-\mbox{\rm Prob}\{\boldsymbol{0}\notin\mathbb{M}+(-r\mathbb{G})|\boldsymbol{0}\notin\mathbb{M}\}=1-\frac{\mbox{\rm Prob}\{\mathbb{M}\cap r\mathbb{G}=\emptyset\}}{\phi}.$

(30)

If one defines the random variable $R=\inf\{ s:\mathbb{M}\cap s\mathbb{G}\neq\emptyset\}$ then $H_{\mathbb{G}}(r)=\mbox{\rm Prob}\{ R\leq r|R>0\}$ [61].

[212.2.1] For the unit ball $\mathbb{G}=\mathbb{B}(\boldsymbol{0},1)$ in three dimensions $H_{\mathbb{B}}$ is called spherical contact distribution. [212.2.2] The quantity $1-H_{\mathbb{B}}(r)$ is then the distribution function of the random distance from a randomly chosen point in $\mathbb{P}$ to its nearest neighbour in $\mathbb{M}$ . [212.2.3] The probability density

$p(r)=\frac{\mbox{\rm d}}{\mbox{\rm d}r}(1-H_{\mathbb{B}}(r))=-\frac{\mbox{\rm d}}{\mbox{\rm d}r}H_{\mathbb{B}}(r)$

(31)

was discussed in [56] as a well defined alternative to the frequently used pore size distrubution from mercury porosimetry.

[212.3.1] For an oriented unit interval $\mathbb{G}=\mathbb{B}^{1}(\boldsymbol{0},1;\boldsymbol{e})$ where $\boldsymbol{e}$ is the a unit vector one obtains the linear contact distribution. [212.3.2] The linear contact distribution written as $L(r\boldsymbol{e})=\phi(1-H_{{\mathbb{B}^{1}(\boldsymbol{0},1;\boldsymbol{e})}}(r))$ is sometimes called lineal path function [70]. [212.3.3] It is related to the chord length distribution $p_{{cl}}(x)$ defined as the probability that an interval in the intersection of $\mathbb{P}$ with a straight line containing $\mathbb{B}^{1}(\boldsymbol{0},1;\boldsymbol{e})$ has length smaller than $x$ [30, 61, p. 208].

3.6 Local Porosity Distributions

[212.3.4] The idea of local porosity distributions is to measure geometric observables inside compact convex subsets $\mathbb{K}\subset\mathbb{S}$ , and to collect the results into empirical histograms [27]. [212.3.5] Let $\mathbb{K}({\boldsymbol{r}},L)$ denote a cube of side length $L$ centered at the lattice vector ${\boldsymbol{r}}$ . [212.3.6] The set $\mathbb{K}({\boldsymbol{r}},L)$ is called a measurement cell. [212.3.7] A geometric observable $f$ , when measured inside a measurement cell $\mathbb{K}({\boldsymbol{r}},L)$ , is denoted as $f({\boldsymbol{r}},L)$ and called a local observable. [212.3.8] An example are local Hadwiger functional densities $f=\sum _{{i=1}}^{d}c_{i}\psi _{i}$ with coefficients $c_{i}$ as in Hadwigers theorem (18). [212.3.9] Here the local quermassintegrals are defined using (12) as

$\psi _{i}(\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L))=\frac{W_{i}(\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L))}{V_{d}(\mathbb{K}({\boldsymbol{r}},L))}$

(32)

for $i=1,\ldots,d$ . [212.3.10] In the following mainly the special case $d=3$ will be of interest. [212.3.11] For $d=3$ the local porosity is defined by setting $i=0$ ,

$\phi({\boldsymbol{r}},L)=\psi _{0}(\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L)).$

(33)

[page 213, §0] [213.0.1] Local densities of surface area, mean curvature and Euler characteristic may be defined analogously. [213.0.2] The local porosity distribution, defined as

$\mu(\phi;{\boldsymbol{r}},L)=\left\langle\delta(\phi-\phi({\boldsymbol{r}},L))\right\rangle,$

(34)

gives the probability density to find a local porosity $\phi({\boldsymbol{r}},L)$ in the measurement cell $\mathbb{K}({\boldsymbol{r}},L)$ . [213.0.3] Here $\delta(x)$ denotes the Dirac $\delta$ -distribution. [213.0.4] The support of $\mu$ is the unit interval. [213.0.5] For noncubic measurement cells $\mathbb{K}$ one defines analogously $\mu(\phi;\mathbb{K})=\left\langle\delta(\phi-\phi(\mathbb{K}))\right\rangle$ where $\phi(\mathbb{K})=\phi(\mathbb{P}\cap\mathbb{K})$ is the local observable in cell $\mathbb{K}$ .

[213.1.1] The concept of local porosity distributions ^c (This is a footnote:) ^cor more generally ‘‘local geometry distributions’’ [28, 30] was introduced in [27] and has been generalized in two directions [30]. [213.1.2] Firstly by admitting more than one measurement cell, and secondly by admitting more than one geometric observable. [213.1.3] The general $n$ -cell distribution function is defined as [30]

	$\displaystyle\mu _{{n;f_{1},\ldots,f_{m}}}(f_{{11}},\ldots,f_{{1n}};\ldots;f_{{m1}},\ldots,f_{{mn}};\mathbb{K}_{1},\ldots,\mathbb{K}_{n})=$
	$\displaystyle\left\langle\delta(f_{{11}}-f_{1}(\mathbb{K}_{1}))\ldots\delta(f_{{1n}}-f_{1}(\mathbb{K}_{n}))\ldots\delta(f_{{m1}}-f_{m}(\mathbb{K}_{1}))\ldots\delta(f_{{mn}}-f_{m}(\mathbb{K}_{n}))\right\rangle$		(35)

for $n$ general measurement cells $\mathbb{K}_{1},\ldots,\mathbb{K}_{n}$ and $m$ observables $f_{1},\ldots,f_{m}$ . [213.1.4] The $n$ -cell distribution is the probability density to find the values $f_{{11}}$ of the local observable $f_{1}$ in cell $\mathbb{K}_{1}$ and $f_{{12}}$ in cell $\mathbb{K}_{2}$ and so on until $f_{{mn}}$ of local observable $f_{m}$ in $\mathbb{K}_{n}$ . [213.1.5] Definition (35) is a broad generalization of (34). [213.1.6] This generalization is not purely academic, but was motivated by problems of fluid flow in porous media where not only $\psi _{0}$ but also $\psi _{1}$ becomes important [28]. [213.1.7] Local quermassintegrals, defined in (32), and their linear combinations (Hadwiger functionals) furnish important examples for local observables in (35), and they have recently been measured [40].

[213.2.1] The general $n$ -cell distribution is very general indeed. [213.2.2] It even contains $p$ from (24) as the special case $m=1,f_{1}=\phi$ and $n=N$ with $\mathbb{K}_{i}=\mathbb{V}_{i}=\mathbb{K}({\boldsymbol{r}}_{i},a)$ . [213.2.3] More precisely one has

$\mu _{{N;\phi}}(\phi _{1},\ldots,\phi _{N};\mathbb{V}_{1},\ldots,\mathbb{V}_{N})=p(\phi _{1},\ldots,\phi _{N})$

(36)

because in that case $\phi _{i}=z_{i}=1$ if $\mathbb{V}_{i}\in\mathbb{P}$ and $\phi _{i}=z_{i}=0$ for $\mathbb{V}\notin\mathbb{P}$ . [213.2.4] In this way it is seen that the very definition of a stochastic geometry is related to local porosity distributions (or more generally local geometry distributions). [213.2.5] As a consequence the general $n$ -cell distribution $\mu _{{n;f_{1},\ldots,f_{m}}}$ is again mainly of theoretical interest, and usually unavailable for practical computations.

[213.3.1] Expectation values with respect to $p$ have generalizations to averages with respect to $\mu$ . [213.3.2] Averaging with respect to $\mu$ will be denoted by an overline. [213.3.3] In the

[page 214, §0] special case $m=1,f_{1}=\phi$ and $\mathbb{K}_{i}=\mathbb{V}_{i}=\mathbb{K}({\boldsymbol{r}}_{i},a)$ with $n<N$ one finds [30]

	$\displaystyle\overline{\phi({\boldsymbol{r}}_{1},a)\cdots\phi({\boldsymbol{r}}_{n},a)}$
	$\displaystyle=\int _{0}^{1}\ldots\int _{0}^{1}\phi _{1}\cdots\phi _{n}\mu _{{n;\phi}}(\phi _{1},\ldots,\phi _{n};\mathbb{V}_{1},\ldots,\mathbb{V}_{n})\mbox{\rm d}\phi _{1}\cdots\mbox{\rm d}\phi _{n}$
	$\displaystyle=\int _{0}^{1}\ldots\int _{0}^{1}\phi _{1}\cdots\phi _{n}\mu _{{N;\phi}}(\phi _{1},\ldots,\phi _{N};\mathbb{V}_{1},\ldots,\mathbb{V}_{N})\mbox{\rm d}\phi _{1}\cdots\mbox{\rm d}\phi _{N}$
	$\displaystyle=\int _{0}^{1}\ldots\int _{0}^{1}\phi _{1}\cdots\phi _{n}\left\langle\delta(\phi _{1}-\phi({\boldsymbol{r}}_{1},a))\cdots\delta(\phi _{N}-\phi({\boldsymbol{r}}_{N},a))\right\rangle\mbox{\rm d}\phi _{1}\cdots\mbox{\rm d}\phi _{N}$
	$\displaystyle=\left\langle\phi({\boldsymbol{r}}_{1},a)\cdots\phi({\boldsymbol{r}}_{n},a)\right\rangle$
	$\displaystyle=\left\langle\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{1})\ldots\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{P}}}({\boldsymbol{r}}_{n})\right\rangle$
	$\displaystyle=S_{n}({\boldsymbol{r}}_{1},\ldots,{\boldsymbol{r}}_{n})$		(37)

thereby identifying the moment functions of order $n$ as averages with respect to an $n$ -cell distribution.

[214.1.1] For practical applications the $1$ -cell local porosity distributions $\mu({\boldsymbol{r}},L)$ and their analogues for other quermassintegrals are of greatest interest. [214.1.2] For a homogeneous medium the local porosity distribution obeys

$\mu(\phi;{\boldsymbol{r}},L)=\mu(\phi;\boldsymbol{0},L)=\mu(\phi;L)$

(38)

for all lattice vectors ${\boldsymbol{r}}$ , i.e. it is independent of the placement of the measurement cell. [214.1.3] A disordered medium with substitutional disorder [71] may be viewed as a stochastic geometry obtained by placing random elements at the cells or sites of a fixed regular substitution lattice. [214.1.4] For a substitutionally disordered medium the local porosity distribution $\mu({\boldsymbol{r}},L)$ is a periodic function of ${\boldsymbol{r}}$ whose period is the lattice constant of the substitution lattice. [214.1.5] For stereological issues in the measurement of $\mu$ from thin sections see [64].

[214.2.1] Averages with respect to $\mu$ are denoted by an overline. [214.2.2] For a homogeneous medium the average local porosity is found as

$\overline{\phi}({\boldsymbol{r}},L)=\int _{0}^{1}\phi\mu(\phi;{\boldsymbol{r}},L)\mbox{\rm d}\phi=\left\langle\phi\right\rangle=\overline{\phi}$

(39)

[page 215, §0] independent of ${\boldsymbol{r}}$ and $L$ . [215.0.1] The variance of local porosities for a homogeneous medium defined in the first equality

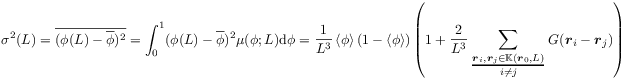$\sigma^{2}(L)=\overline{(\phi(L)-\overline{\phi})^{2}}=\int _{0}^{1}(\phi(L)-\overline{\phi})^{2}\mu(\phi;L)\mbox{\rm d}\phi=\frac{1}{L^{3}}\left\langle\phi\right\rangle(1-\left\langle\phi\right\rangle)\left(1+\frac{2}{L^{3}}\sum _{{\genfrac{}{}{1.0pt}{1}{{\boldsymbol{r}}_{i},{\boldsymbol{r}}_{j}\in\mathbb{K}({\boldsymbol{r}}_{0},L)}{i\neq j}}}G({\boldsymbol{r}}_{i}-{\boldsymbol{r}}_{j})\right)$

(40)

is related to the correlation function as given in the second equality [30]. [215.0.2] The skewness of the local porosity distribution is defined as the average

$\kappa _{3}(L)=\frac{\overline{(\phi(L)-\overline{\phi})^{3}}}{\sigma(L)^{3}}.$

(41)

[215.1.1] The limits $L\to 0$ and $L\rightarrow\infty$ of small resp. large measurement cells are of special interest. [215.1.2] In the first case one reaches the limiting resolution at $L=a$ and finds for a homogeneous medium [27, 30]

$\mu(\phi;a)=\overline{\phi}\delta(\phi-1)-(1-\overline{\phi})\delta(\phi).$

(42)

[215.1.3] The limit $L\rightarrow\infty$ is more intricate because it requires also the limit $\mathbb{S}\to\mathbb{R}^{3}$ . [215.1.4] For a homogeneous medium (40) shows $\sigma(L)\to 0$ for $L\to 0$ and this suggests

$\mu(\phi,L\rightarrow\infty)=\delta(\phi-\overline{\phi}).$

(43)

[215.1.5] For macroscopically heterogeneous media, however, the limiting distribution may deviate from this result [30]. [215.1.6] If (43) holds then in both limits the geometrical information contained in $\mu$ reduces to the single number $\overline{\phi}=\left\langle\phi\right\rangle$ . [215.1.7] If (42) and (43) hold there exists a special length scale $L^{*}$ defined as

$L^{*}=\min\{ L:\mu(0;L)=\mu(1;L)=0\}$

(44)

at which the $\delta$ -components at $\phi=0$ and $\phi=1$ vanish. [215.1.8] In the examples below the length $L^{*}$ is a measure for the size of pores.

[215.2.1] The ensemble picture underlying the definition of a stochastic medium is an idealization. [215.2.2] In practice one is given only a single realization and has to resort to an ergodic hypothesis for obtaining an estimate of the local porosity distributions. [215.2.3] In the examples below the local porosity distribution is estimated by

$\widetilde{\mu}(\phi;L)=\frac{1}{m}\sum _{{{\boldsymbol{r}}}}\delta(\phi-\phi({\boldsymbol{r}},L))$

(45)

where $m$ is the number of placements of the measurement cell $\mathbb{K}({\boldsymbol{r}},L)$ . [215.2.4] Ideally the measurement cells should be far apart or at least nonoverlapping, but in

[page 216, §0] practice this restriction cannot be observed because the samples are not large enough. [216.0.1] In the results presented below $\mathbb{K}({\boldsymbol{r}},L)$ is placed on all lattice sites which are at least a distance $L/2$ from the boundary of $\mathbb{S}$ . [216.0.2] This allows for

$m=\prod _{{i=1}}^{3}(M_{i}-L+1)$

(46)

placements of $\mathbb{K}({\boldsymbol{r}},L)$ in a sample with side lengths $M_{1},M_{2},M_{3}$ . [216.0.3] The use of $\widetilde{\mu}$ instead of $\mu$ can lead to deviations due to violations of the ergodic hypothesis or simply due to oversampling the central regions of $\mathbb{S}$ [10, 11].

3.7 Local Percolation Probabilities

[216.0.4] Transport and propagation in porous media are controlled by the connectivity of the pore space. [216.0.5] Local percolation probabilities characterize the connectivity [27]. [216.0.6] Their calculation requires a threedimensional pore space representation, and early results were restricted to samples reconstructed laboriously from sequential thin sectioning [32].

[216.1.1] Consider the functional $\Lambda:{\mathcal{K}}\times{\mathcal{K}}\times{\mathcal{R}}\to\mathbb{Z}_{2}=\{ 0,1\}$ defined by

$\Lambda({\mathbb{K}_{0}},{\mathbb{K}_{\infty}};\mathbb{P}\cap\mathbb{S})=\begin{cases}1:\text{~if~}{\mathbb{K}_{0}}\leadsto{\mathbb{K}_{\infty}}\text{~in~}\mathbb{P}\\ 0:\text{~otherwise}\end{cases}$

(47)

where ${\mathbb{K}_{0}}\subset\mathbb{R}^{3},{\mathbb{K}_{\infty}}\subset\mathbb{R}^{3}$ are two compact convex sets with ${\mathbb{K}_{0}}\cap(\mathbb{P}\cap\mathbb{S})\neq\emptyset$ and ${\mathbb{K}_{\infty}}\cap(\mathbb{P}\cap\mathbb{S})\neq\emptyset$ , and ‘‘ ${\mathbb{K}_{0}}\leadsto{\mathbb{K}_{\infty}}$ in $\mathbb{P}$ ’’ means that there is a path connecting ${\mathbb{K}_{0}}$ and ${\mathbb{K}_{\infty}}$ that lies completely in $\mathbb{P}$ . [216.1.2] In the examples below the sets ${\mathbb{K}_{0}}$ and ${\mathbb{K}_{\infty}}$ correspond to opposite faces of the sample, but in general other choices are allowed. [216.1.3] Analogous to $\Lambda$ defined for the whole sample one defines for a measurement cell

$\Lambda _{\alpha}({\boldsymbol{r}},L)=\Lambda({\mathbb{K}_{0}}_{\alpha},{\mathbb{K}_{\infty}}_{\alpha};\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L))=\begin{cases}1:\text{~if~}{\mathbb{K}_{0}}_{\alpha}\leadsto{\mathbb{K}_{\infty}}_{\alpha}\text{~in~}\mathbb{P}\\ 0:\text{~otherwise}\end{cases}$

(48)

where $\alpha=x,y,z$ and ${\mathbb{K}_{0}}_{x},{\mathbb{K}_{\infty}}_{x}$ denote those two faces of $\mathbb{K}({\boldsymbol{r}},L)$ that are normal to the $x$ direction. [216.1.4] Similarly ${\mathbb{K}_{0}}_{y},{\mathbb{K}_{\infty}}_{y},{\mathbb{K}_{0}}_{z}{\mathbb{K}_{\infty}}_{z}$ denote the faces of $\mathbb{K}({\boldsymbol{r}},L)$ normal to the $y$ - and $z$ -directions. [216.1.5] Two additional percolation observables $\Lambda _{3}$ and $\Lambda _{c}$ are introduced by

$\displaystyle\Lambda _{3}({\boldsymbol{r}},L)$	$\displaystyle=\Lambda _{x}({\boldsymbol{r}},L)\Lambda _{y}({\boldsymbol{r}},L)\Lambda _{z}({\boldsymbol{r}},L)$		(49)
$\displaystyle\Lambda _{c}({\boldsymbol{r}},L)$	$\displaystyle=sgn(\Lambda _{x}({\boldsymbol{r}},L)+\Lambda _{y}({\boldsymbol{r}},L)+\Lambda _{z}({\boldsymbol{r}},L)).$		(50)

[216.1.6] $\Lambda _{3}$ indicates that the cell is percolating in all three directions while $\Lambda _{c}$ indicates percolation in $x$ - or $y$ - $z$ -direction. [216.1.7] The local percolation probabilities are defined as

$\lambda _{\alpha}(\phi;L)=\frac{\sum _{{\boldsymbol{r}}}\Lambda _{\alpha}({\boldsymbol{r}},L)\delta _{{\phi,\phi({\boldsymbol{r}},L)}}}{\sum _{{\boldsymbol{r}}}\delta _{{\phi,\phi({\boldsymbol{r}},L)}}}$

(51)

[page 217, §0] where

$\delta _{{\phi,\phi({\boldsymbol{r}},L)}}=\begin{cases}1:\text{~if~}\phi=\phi({\boldsymbol{r}},L)\\ 0:\text{~otherwise}.\end{cases}$

(52)

[217.0.1] The local percolation probability $\lambda _{\alpha}(\phi;L)$ gives the fraction of measurement cells of sidelength $L$ with local porosity $\phi$ that are percolating in the ‘‘ $\alpha$ ’’-direction. [217.0.2] The total fraction of cells percolating along the ‘‘ $\alpha$ ’’-direction is then obtained by integration

$p_{\alpha}(L)=\int _{0}^{1}\mu(\phi;L)\lambda _{\alpha}(\phi;L)\mbox{\rm d}\phi.$

(53)

[217.0.3] This geometric observable is a quantitative measure for the number of elements that have to be percolating if the pore space geometry is approximated by a substitutionally disordered lattice or network model. [217.0.4] Note that neither $\Lambda$ nor $\Lambda _{\alpha}$ are additive functionals, and hence local percolation probabilities have nothing to do with Hadwigers theorem.

[217.1.1] It is interesting that there is a relation between the local percolation probabilities and the local Euler characteristic $V_{0}(\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},l))$ . [217.1.2] The relation arises from the observation that the voxels $\mathbb{V}_{i}$ are closed, convex sets, and hence for any two voxels $\mathbb{V}_{i},\mathbb{V}_{j}$ the Euler characteristic of their intersection

$V_{0}(\mathbb{V}_{i}\cap\mathbb{V}_{j})=\begin{cases}1:\text{~if~}\mathbb{V}_{i}\cap\mathbb{V}_{j}\neq\emptyset\\ 0:\text{~if~}\mathbb{V}_{i}\cap\mathbb{V}_{j}=\emptyset\end{cases}$

(54)

indicates whether two voxels are nearest neighbours. [217.1.3] A measurement cell $\mathbb{K}({\boldsymbol{r}},L)$ contains $L^{3}$ voxels. [217.1.4] It is then possible to construct a $(L^{3}+2)\times(L^{3}+2)^{2}$ -matrix $B$ with matrix elements

$\displaystyle(B)_{{i\;(i,j)}}$	$\displaystyle=V_{0}(\mathbb{V}_{i}\cap\mathbb{V}_{j})$		(55)
$\displaystyle(B)_{{i\;(j,i)}}$	$\displaystyle=-V_{0}(\mathbb{V}_{i}\cap\mathbb{V}_{j})$		(56)

where $i,j\in\{ 0,1,\ldots,L^{3},\infty\}$ and the sets $\mathbb{V}_{0}={\mathbb{K}_{0}}$ and $\mathbb{V}_{\infty}={\mathbb{K}_{\infty}}$ are two opposite faces of the measurement cell. [217.1.5] The rows in the matrix $B$ correspond to voxels while the columns correspond to voxel pairs. [217.1.6] Define the matrix $A=BB^{T}$ where $B^{T}$ is the transpose of $B$ . [217.1.7] The diagonal elements $(A)_{{ii}}$ give the number of voxels to which the voxel $\mathbb{V}_{i}$ is connected. [217.1.8] A matrix element $(A)_{{ij}}$ differs from zero if and only if $\mathbb{V}_{i}$ and $\mathbb{V}_{j}$ are connected. [217.1.9] Hence the matrix $A$ reflects the local connectedness of the pore space around a single voxel. [217.1.10] Sufficiently high powers of $A$ provide information about the global connectedness of $\mathbb{P}$ . [217.1.11] One finds

$\Lambda({\mathbb{K}_{0}},{\mathbb{K}_{\infty}};\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L))=sgn\left(|(A^{m})_{{0\infty}}|\right)$

(57)

where $(A^{m})_{{0\infty}}$ is the matrix element in the upper right hand corner and $m$ is arbitrary subject to the condition $m>L^{3}$ . [217.1.12] The set $\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L)$ can always be decomposed uniquely into pairwise disjoint connectedness components (clusters)

[page 218, §0] $\mathbb{B}_{i}$ whose number is given by the rank of $B$ . [218.0.1] Hence

$V_{0}(\mathbb{P}\cap\mathbb{K}({\boldsymbol{r}},L))=\sum _{{i=1}}^{{\mbox{\scriptsize rank}B}}V_{0}(\mathbb{B}_{i})$

(58)

provides an indirect connection between the local Euler characteristic and the local percolation probabilities mediated by the matrix $B$ . ^d (This is a footnote:) ^dFor percolation systems it has been conjectured that the zero of the Euler characteristic as a function of the occupation probability is an approximation to the percolation threshold [45])

Author:	R. Hilfer
originally published in:	Räumliche Statistik und Statistische Physik, Lecture Notes in Physics Vol. 554, Springer, Berlin, page 203-241 (2000), ISBN - -
originally published:	2000