4 Stochastic Reconstruction of Microstructures
4.1 Description of Experimental Sample
[218.0.2] The experimental sample, denoted as ![]() , is a
threedimensional microtomographic
image of Fontainebleau sandstone.
[218.0.3] This sandstone is a popular reference standard because of its
chemical, crystallographic and microstructural simplicity
[14, 13].
[218.0.4] Fontainebleau sandstone consists of monocrystalline quartz
grains that have been eroded for long periods before being
deposited in dunes along the sea shore during the Oligocene,
roughly 30 million years ago.
[218.0.5] It is well sorted containing grains of around
, is a
threedimensional microtomographic
image of Fontainebleau sandstone.
[218.0.3] This sandstone is a popular reference standard because of its
chemical, crystallographic and microstructural simplicity
[14, 13].
[218.0.4] Fontainebleau sandstone consists of monocrystalline quartz
grains that have been eroded for long periods before being
deposited in dunes along the sea shore during the Oligocene,
roughly 30 million years ago.
[218.0.5] It is well sorted containing grains of around
![]() in diameter.
[218.0.6] The sand was cemented by silica crystallizing around the grains.
[218.0.7] Fontainebleau sandstone exhibits intergranular porosity ranging
from
in diameter.
[218.0.6] The sand was cemented by silica crystallizing around the grains.
[218.0.7] Fontainebleau sandstone exhibits intergranular porosity ranging
from ![]() to roughly
to roughly ![]() [13].
[13].
| Properties | ||||
|---|---|---|---|---|
| 300 | 255 | 256 | 256 | |
| 300 | 255 | 256 | 256 | |
| 299 | 255 | 256 | 256 | |
| 0.1355 | 0.1356 | 0.1421 | 0.1354 | |
| 10.4 mm |
10.9 mm |
16.7 mm |
11.06 mm |
|
| 35 | 25 | 23 | 27 | |
| 0.0045 | 0.0239 | 0.3368 | 0.3527 |
[218.1.1] The computer assisted microtomography was carried out on a
micro-plug drilled from a larger original core.
[218.1.2] The original core from which the micro-plug was taken had a measured
porosity of ![]() , permability of
, permability of ![]() and
formation factor
and
formation factor ![]() .
[218.1.3] The porosity
.
[218.1.3] The porosity ![]() of the microtomographic data set
is only
of the microtomographic data set
is only ![]() (see Table 2).
[218.1.4] The difference between the porosity of the original core and that
of the final data set is due to the heterogeneity of the sandstone and
to the difference in sample size.
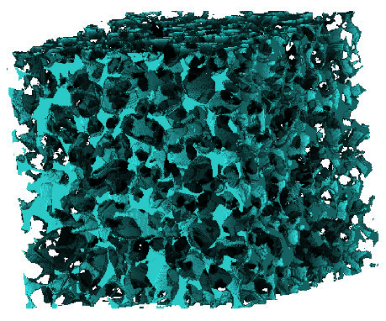
[218.1.5] The experimental sample is referred to as EX in the
following.
[218.1.6] The pore space of the experimental sample is visualized
in Figure 1.
(see Table 2).
[218.1.4] The difference between the porosity of the original core and that
of the final data set is due to the heterogeneity of the sandstone and
to the difference in sample size.
[218.1.5] The experimental sample is referred to as EX in the
following.
[218.1.6] The pore space of the experimental sample is visualized
in Figure 1.
[page 219, §0]

[page 220, §1]
4.2 Sedimentation, Compaction and Diagenesis Model
[220.1.1] Fontainebleau sandstone is the result of complex physical, chemical and geological processes known as sedimentation, compaction and diagenesis. [220.1.2] It is therefore natural to model these processes directly rather than trying to match general geometrical characteristics. [220.1.3] This conclusion was also obtained from local porosity theory for the cementation index in Archie’s law [27]. [220.1.4] The diagenesis model abbreviated as DM in the following, attempts model the main geological sandstone-forming processes [4, 48].
[220.2.1] In a first step porosity, grain size distribution, a visual estimate of the degree of compaction, the amount of quartz cement and clay contents and texture are obtained by image analysis of backscattered electron/cathodo-luminescence images made from thin sections. [220.2.2] The sandstone modeling is then carried out in three main steps: grain sedimentation, compaction and diagenesis described in detail in [4, 48].
[220.3.1] Sedimentation begins by measuring the grain size distribution using an erosion-dilation algorithm. [220.3.2] Then spheres with random diameters are picked randomly according to the grain size distribution. [220.3.3] They are dropped onto the grain bed and relaxed into a local potential energy minimum or, alternatively, into the global minimum.
[220.4.1] Compaction occurs because the sand becomes buried into
the subsurface.
[220.4.2] Compaction reduces the bulk volume (and porosity).
[220.4.3] It is modelled as a linear process in which the vertical coordinate
of every sandgrain is shifted vertically downwards by an amount
proportional to the original vertical position.
[220.4.4] The proportionality constant is called the compaction factor.
[220.4.5] Its value for the Fontainebleau sample is estimated to be
![]() from thin section analysis.
from thin section analysis.
[220.5.1] In the diagenesis part
only a subset of known diagenetical processes are simulated,
namely quartz cement overgrowth and precipitation of authigenic
clay on the free surface.
[220.5.2] Quartz cement overgrowth is modeled by radially enlarging each grain.
[220.5.3] If ![]() denotes the radius of the originally deposited spherical
grain, its new radius along the direction
denotes the radius of the originally deposited spherical
grain, its new radius along the direction ![]() from grain center
is taken to be [59, 48]
from grain center
is taken to be [59, 48]
| (59) |
where ![]() is the distance between the surface of the
original spherical grain and the surface of its Voronoi
polyhedron along the direction
is the distance between the surface of the
original spherical grain and the surface of its Voronoi
polyhedron along the direction ![]() .
[220.5.4] The constant
.
[220.5.4] The constant ![]() controls the amount of cement, and the
growth exponent
controls the amount of cement, and the
growth exponent ![]() controls the type of cement overgrowth.
[220.5.5] For
controls the type of cement overgrowth.
[220.5.5] For ![]() the cement grows preferentially
into the pore bodies, for
the cement grows preferentially
into the pore bodies, for ![]() it grows concentrically,
and for
it grows concentrically,
and for ![]() quartz cement grows towards the pore
throats [48].
[220.5.6] Authigenic clay growth
is simulated by precipitating clay voxels on the free mineral surface.
The clay texture may be pore-lining or pore-filling or a combination of
the two.
quartz cement grows towards the pore
throats [48].
[220.5.6] Authigenic clay growth
is simulated by precipitating clay voxels on the free mineral surface.
The clay texture may be pore-lining or pore-filling or a combination of
the two.
[220.6.1] The parameters for modeling the Fontainebleau sandstone
were ![]() for the compaction factor, and
for the compaction factor, and
![]() and
and ![]() for the cementation parameters.
[220.6.2] The resulting model configuration of the sample DM is
displayed in Figure 2.
for the cementation parameters.
[220.6.2] The resulting model configuration of the sample DM is
displayed in Figure 2.
[page 221, §0]


[page 222, §1]
4.3 Gaussian Field Reconstruction Model
[222.1.1] A stochastic reconstruction model attempts to
approximate a given experimental sample by a randomly
generated model structure that matches prescribed
stochastic properties of the experimental sample.
[222.1.2] In this and the next section the stochastic property
of interest is the correlation function ![]() of
the Fontainebleau sandstone.
of
the Fontainebleau sandstone.
[222.2.1] The Gaussian field (GF) reconstruction model
tries to match a reference correlation function by
filtering Gaussian random variables [49, 2, 1, 69].
[222.2.2] Given the reference correlation function ![]() and
porosity
and
porosity ![]() of the experimental sample
the Gaussian field method proceeds in three main steps:
of the experimental sample
the Gaussian field method proceeds in three main steps:
Initially a Gaussian field
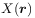 is generated consisting of
statistically independent Gaussian random variables
is generated consisting of
statistically independent Gaussian random variables 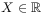 at each
lattice point
at each
lattice point 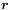 .
.[222.2.3] The field
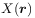 is first passed through a linear filter
which produces a correlated Gaussian field
is first passed through a linear filter
which produces a correlated Gaussian field 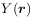 with
zero mean and unit variance.
[222.2.4] The reference correlation function
with
zero mean and unit variance.
[222.2.4] The reference correlation function 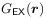 and porosity
and porosity
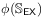 enter into the mathematical construction
of this linear filter.
enter into the mathematical construction
of this linear filter.[222.2.5] The correlated field
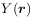 is then passed through a nonlinear
discretization filter which produces the reconstructed sample
is then passed through a nonlinear
discretization filter which produces the reconstructed sample 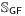 .
.
[222.2.6] Step 4.3 is costly because it requires the solution of a very large set of non-linear equations. [222.2.7] A computationally more efficient method uses Fourier Transformation [1]. [222.2.8] The linear filter in step 4.3 is defined in Fourier space through
| (60) |
where ![]() is the sidelength of a cubic sample,
is the sidelength of a cubic sample,
![]() is a normalisation factor, and
is a normalisation factor, and
| (61) |
denotes the Fourier transform of ![]() .
[222.2.9] Similarly
.
[222.2.9] Similarly ![]() is the Fourier transform of
is the Fourier transform of ![]() ,
and
,
and ![]() is the Fourier transform of the correlation
function
is the Fourier transform of the correlation
function ![]() .
[222.2.10]
.
[222.2.10] ![]() has to be computed by an
inverse process from the correlation function
has to be computed by an
inverse process from the correlation function
![]() and porosity of the experimental reference
(details in [1]).
and porosity of the experimental reference
(details in [1]).
[222.3.1] The Gaussian field reconstruction requires a large separation
![]() where
where ![]() is the
correlation length of the experimental reference, and
is the
correlation length of the experimental reference, and ![]() is the number of sites.
[222.3.2]
is the number of sites.
[222.3.2] ![]() is defined as the length such that
is defined as the length such that
![]() for
for ![]() .
[222.3.3] If the condition
.
[222.3.3] If the condition ![]() is violated then step 4.3
of the reconstruction fails in the sense that the correlated
Gaussian field
is violated then step 4.3
of the reconstruction fails in the sense that the correlated
Gaussian field ![]() does not have zero mean and unit variance.
[222.3.4] In such a situation the filter
does not have zero mean and unit variance.
[222.3.4] In such a situation the filter ![]() will differ from the
Fourier transform of the correlation function of the
will differ from the
Fourier transform of the correlation function of the ![]() .
[222.3.5] It is also difficult to calculate
.
[222.3.5] It is also difficult to calculate ![]() accurately near
accurately near ![]() [1].
[222.3.6] This leads to a discrepancy at small
[1].
[222.3.6] This leads to a discrepancy at small ![]() between
between ![]() and
and
![]() .
[222.3.7] The problem can be overcome by choosing large
.
[222.3.7] The problem can be overcome by choosing large ![]() .
[222.3.8] However, in
.
[222.3.8] However, in ![]() very large
very large ![]() also demands prohibitively
large memory.
[222.3.9] In
also demands prohibitively
large memory.
[222.3.9] In
[page 223, §0]


[page 224, §0]
earlier work [2, 1] the correlation function
![]() was sampled down to a lower resolution, and
the reconstruction algorithm then proceeded with such a
rescaled correlation function.
[224.0.1] This leads to a reconstructed sample
was sampled down to a lower resolution, and
the reconstruction algorithm then proceeded with such a
rescaled correlation function.
[224.0.1] This leads to a reconstructed sample ![]() which
also has a lower resolution.
[224.0.2] Such reconstructions have lower average connectivity
compared to the original model [9]
For a quantitative comparison with the
microstructure of
which
also has a lower resolution.
[224.0.2] Such reconstructions have lower average connectivity
compared to the original model [9]
For a quantitative comparison with the
microstructure of ![]() it is necessary to retain the
original level of resolution,
and to use the original correlation
function
it is necessary to retain the
original level of resolution,
and to use the original correlation
function ![]() without subsampling.
[224.0.3] Because
without subsampling.
[224.0.3] Because ![]() is nearly
is nearly ![]() for
for ![]()
![]() was truncated at
was truncated at ![]() to save computer time.
[224.0.4] The resulting configuration
to save computer time.
[224.0.4] The resulting configuration ![]() with
with ![]() is displayed in Figure 3.
is displayed in Figure 3.
4.4 Simulated Annealing Reconstruction Model
[224.0.5] The simulated annealing (SA) reconstruction model is a
second method to generate a threedimensional random microstructure
with prescribed porosity and correlation function.
[224.0.6] The method generates a configuration ![]() by minimizing
the deviations between
by minimizing
the deviations between ![]() and a predefined reference
function
and a predefined reference
function ![]() .
[224.0.7] Note that the generated configuration
.
[224.0.7] Note that the generated configuration
![]() is not unique and hence other modeling aspects
come into play [42].
[224.0.8] Below,
is not unique and hence other modeling aspects
come into play [42].
[224.0.8] Below, ![]() is again the correlation function
of the Fontainebleau sandstone.
is again the correlation function
of the Fontainebleau sandstone.
[224.1.1] An advantage of the simulated annealing method over the Gaussian field method is that it can also be used to match other quantities besides the correlation function. [224.1.2] Examples would be the linear or spherical contact distributions [42]. [224.1.3] On the other hand the method is computationally very demanding, and cannot be implemented fully at present. [224.1.4] A simplified implementation was discussed in [70], and is used below.
[224.2.1] The reconstruction is performed on a cubic lattice with side length
![]() and lattice spacing
and lattice spacing ![]() .
[224.2.2] The lattice is initialized randomly with
.
[224.2.2] The lattice is initialized randomly with ![]() ’s and
’s and ![]() ’s such that
the volume fraction of
’s such that
the volume fraction of ![]() ’s equals
’s equals ![]() .
[224.2.3] This porosity is preserved throughout the simulation.
[224.2.4] For the sake of numerical efficiency the autocorrelation
function is evaluated in a simplified form using [70]
.
[224.2.3] This porosity is preserved throughout the simulation.
[224.2.4] For the sake of numerical efficiency the autocorrelation
function is evaluated in a simplified form using [70]
| (62) |
where ![]() are the unit vectors in direction of the
coordinate axes,
are the unit vectors in direction of the
coordinate axes, ![]() ,
and where a tilde
,
and where a tilde ![]() is used to indicate the
directional restriction.
[224.2.5] The sum
is used to indicate the
directional restriction.
[224.2.5] The sum ![]() runs over all
runs over all ![]() lattice sites
lattice sites ![]() with periodic boundary conditions, i.e.
with periodic boundary conditions, i.e. ![]() is evaluated modulo
is evaluated modulo ![]() .
.
[224.3.1] A simulated annealing algorithm is used to minimize the "energy" function
| (63) |
defined as the sum of the squared deviations of ![]() from the
experimental correlation function
from the
experimental correlation function ![]() .
[224.3.2] Each update starts with the exchange of two pixels, one
.
[224.3.2] Each update starts with the exchange of two pixels, one
[page 225, §0]


[page 226, §0]
from pore
space, one from matrix space.
[226.0.1] Let ![]() denote the number of the proposed update step.
[226.0.2] Introducing an acceptance parameter
denote the number of the proposed update step.
[226.0.2] Introducing an acceptance parameter ![]() , which may be interpreted as an
, which may be interpreted as an
![]() -dependent temperature, the proposed configuration is accepted with
probability
-dependent temperature, the proposed configuration is accepted with
probability
| (64) |
[226.0.3] Here the energy and the correlation function of the
configuration is denoted as ![]() and
and ![]() , respectively.
[226.0.4] If the proposed move is rejected, then the old configuration is restored.
, respectively.
[226.0.4] If the proposed move is rejected, then the old configuration is restored.
[226.1.1] A configuration with correlation ![]() is found by lowering
is found by lowering ![]() .
[226.1.2] At low
.
[226.1.2] At low ![]() the system approaches a configuration that minimizes
the energy function.
[226.1.3] In the simulations
the system approaches a configuration that minimizes
the energy function.
[226.1.3] In the simulations ![]() was lowered with
was lowered with ![]() as
as
| (65) |
[226.1.4] The simulation was stopped when 20000 consecutive updates were rejected.
[226.1.5] This happened after
![]() updates
(
updates
(![]() steps per site).
[226.1.6] The resulting configuration
steps per site).
[226.1.6] The resulting configuration ![]() for the simulated annealing
reconstruction is displayed in Figure 4.
for the simulated annealing
reconstruction is displayed in Figure 4.
[226.2.1] A complete evaluation of the correlation function as defined in (29) for a threedimensional system requires so much computer time, that it cannot be carried out at present. [226.2.2] Therefore the algorithm was simplified to increase its speed [70]. [226.2.3] In the simplified algorithm the correlation function is only evaluated along the directions of the coordinate axes as indicated in (62). [226.2.4] The original motivation was that for isotropic systems all directions should be equivalent [70]. [226.2.5] However, it was found in [41] that as a result of this simplification the reconstructed sample may become anisotropic. [226.2.6] In the simplified algorithm the correlation function of the reconstruction deviates from the reference correlation function in all directions other than those of the axes [41]. [226.2.7] The problem is illustrated in Figures 5(a) and 5(b) in two dimensions for a reference correlation function given as
| (66) |
[226.2.8] In Figure 5(a) the correlation function was
matched only in the direction of the ![]() - and
- and ![]() -axis.
[226.2.9] In Figure 5(b) the correlation function was
matched also along the diagonal directions obtained by
rotating the axes 45 degrees.
[226.2.10] The differences in isotropy of the two reconstructions
are clearly visible.
[226.2.11] In the special case of the correlation function of the
Fontainebleau sandstone, however, this effect seems to be
smaller.
[226.2.12] The Fontainebleau correlation function is given in Figure 7
below.
[226.2.13] Figure 6(a) and 6(b) show the result
of twodimensional reconstructions along the axes only
and along axes plus diagonal directions.
[226.2.14] The differences in isotropy seem to be less
pronounced.
[226.2.15] Perhaps this is due to the fact that the Fontainebleau
correlation function has no maxima and minima.
-axis.
[226.2.9] In Figure 5(b) the correlation function was
matched also along the diagonal directions obtained by
rotating the axes 45 degrees.
[226.2.10] The differences in isotropy of the two reconstructions
are clearly visible.
[226.2.11] In the special case of the correlation function of the
Fontainebleau sandstone, however, this effect seems to be
smaller.
[226.2.12] The Fontainebleau correlation function is given in Figure 7
below.
[226.2.13] Figure 6(a) and 6(b) show the result
of twodimensional reconstructions along the axes only
and along axes plus diagonal directions.
[226.2.14] The differences in isotropy seem to be less
pronounced.
[226.2.15] Perhaps this is due to the fact that the Fontainebleau
correlation function has no maxima and minima.
[page 227, §0]


