Sie sind hier: ICP » R. Hilfer » Publikationen

Appendix A Definition of H-functions

[3.2.3.1] The general H-function is defined as the inverse Mellin transform [24]

\hbox{$\displaystyle H^{{mn}}_{{PQ}}\left(z\left|\begin{array}[]{ccc}(a_{1},A_{1})&...&(a_{P},A_{P})\\ (b_{1},B_{1})&...&(b_{Q},B_{Q})\end{array}\right.\right)=$}\frac{1}{2\pi i}\int _{{\mathcal{C}}}\frac{\prod _{{j=1}}^{{m}}\Gamma(b_{j}+B_{j}s)\,\prod _{{j=1}}^{{n}}\Gamma(1-a_{j}-A_{j}s)}{\prod _{{j=m+1}}^{{Q}}\Gamma(1-b_{j}-B_{j}s)\,\prod _{{j=n+1}}^{{P}}\Gamma(a_{j}+A_{j}s)}\; z^{{-s}}\, ds (A.1)

where the contour {\mathcal{C}} runs from c-i\infty to c+i\infty separating the poles of \Gamma(b_{j}+B_{j}s),\;(j=1,...,m) from those of \Gamma(1-a_{j}-A_{j}s),\;(j=1,...,n). [3.2.3.2] Empty products are interpreted as unity. [3.2.3.3] The integers m,n,P,Q satisfy 0\leq m\leq Q and 0\leq n\leq P. [3.2.3.4] The coefficients A_{j} and B_{j} are positive real numbers and the complex parameters a_{j},b_{j} are such that no poles in the integrand coincide. [3.2.3.5] If

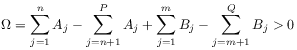\Omega=\sum _{{j=1}}^{{n}}A_{j}-\sum _{{j=n+1}}^{{P}}A_{j}+\sum _{{j=1}}^{{m}}B_{j}-\sum _{{j=m+1}}^{{Q}}B_{j}>0 (A.2)

[page 4, §0]    then the integral converges absolutely and defines the H-function in the sector |{\rm arg}z|\!\!<\Omega\pi/2. [4.1.0.1] The H-function is also well defined when either

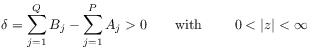\delta=\sum _{{j=1}}^{{Q}}B_{j}-\sum _{{j=1}}^{{P}}A_{j}>0\text{\qquad with \qquad}0<|z|<\infty (A.3)

or

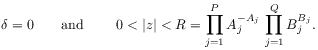\delta=0\text{\qquad and \qquad}0<|z|<R=\prod _{{j=1}}^{{P}}A_{{j}}^{{-A_{j}}}\,\prod _{{j=1}}^{{Q}}B_{j}^{{B_{j}}}. (A.4)

[4.1.0.2] For \delta\geq 0 the H-function has the series representation

\hbox{$\displaystyle H^{{mn}}_{{PQ}}\left(z\left|\begin{array}[]{ccc}(a_{1},A_{1})&...&(a_{P},A_{P})\\ (b_{1},B_{1})&...&(b_{Q},B_{Q})\end{array}\right.\right)=$}\sum _{{i=1}}^{m}\sum _{{k=0}}^{\infty}\frac{\prod\limits _{{\substack{j=1\\ j\neq i}}}^{{m}}\Gamma\left(b_{j}-(b_{i}+k)\frac{B_{j}}{B_{i}}\right)\prod\limits _{{j=1}}^{{n}}\Gamma\left(1-a_{j}+(b_{i}+k)\frac{A_{j}}{B_{i}}\right)}{\prod\limits _{{j=m+1}}^{{Q}}\Gamma\left(1-b_{j}+(b_{i}+k)\frac{B_{j}}{B_{i}}\right)\prod\limits _{{j=n+1}}^{{P}}\Gamma\left(a_{j}-(b_{i}+k)\frac{A_{j}}{B_{i}}\right)}\frac{(-1)^{k}z^{{(b_{i}+k)/B_{i}}}}{k!B_{i}} (A.5)

provided that B_{k}(b_{j}+l)\neq B_{j}(b_{k}+s) for j\neq k,1\leq j,k\leq m and l,s=0,1,... [4.1.0.3] The H-function is a generalization of Meijers G-function and many of the known special functions are special cases of it.