2 Relation between fractional and fractal walks

[1.3.3.1] Let us start by recalling briefly the general theory of continuous time random walks [5, 7, 8]. [1.3.3.2] The basic equation of motion is the continous time random walk (CTRW) integral equation [16]

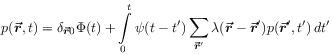$p(\bm{\vec{r}},t)=\delta _{{\bm{\vec{r}}0}}\Phi(t)+\int _{0}^{t}\psi(t-t^{\prime})\sum _{{\bm{\vec{r}}^{\prime}}}\lambda(\bm{\vec{r}}-\bm{\vec{r}}^{\prime})p(\bm{\vec{r}}^{\prime},t^{\prime})\, dt^{\prime}$

(2.1)

[page 2, §0] describing a random walk in continous time without correlation between its spatial and temporal behaviour. [2.1.0.1] Here, as in (1.2), $p(\bm{\vec{r}},t)$ denotes the probability density to find the diffusing entity at the position $\bm{\vec{r}}\in{\mathbb{R}}^{d}$ at time $t$ if it started from the origin $\bm{\vec{r}}=0$ at time $t=0$ . [2.1.0.2] $\lambda(\bm{\vec{r}})$ is the probability for a displacement $\bm{\vec{r}}$ in each single step, and $\psi(t)$ is the waiting time distribution giving the probability density for the time interval $t$ between two consecutive steps. [2.1.0.3] The transition probabilities obey $\sum _{{\bm{\vec{r}}}}\lambda(\bm{\vec{r}})=1$ . [2.1.0.4] The function $\Phi(t)$ is the survival probability at the initial position which is related to the waiting time distribution through

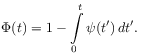$\Phi(t)=1-\int _{0}^{t}\psi(t^{\prime})\, dt^{\prime}.$

(2.2)

[2.1.0.5] The objective of this paper which was defined in the introduction is to show that the fractional master equation (1.2) is a special case of the CTRW-equation (2.1), and to find the appropriate waiting time density.

[2.1.1.1] The translation invariant form of the transition probabilities in (2.1) allows a solution through Fourier-Laplace transformation. [2.1.1.2] Let

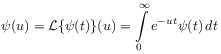$\psi(u)=\mathcal{L}\{\psi(t)\}(u)=\int _{0}^{\infty}e^{{-ut}}\psi(t)\, dt$

(2.3)

denote the Laplace transform of $\psi(t)$ and

$\lambda(\bm{\vec{q}})=\mathcal{F}\{\lambda(\bm{\vec{r}})\}(\bm{\vec{q}})=\sum _{{\bm{\vec{r}}}}e^{{i\bm{\vec{q}}\cdot\bm{\vec{r}}}}\lambda(\bm{\vec{r}})$

(2.4)

the Fourier transform of $\lambda(\bm{\vec{r}})$ , which is also called the structure function of the random walk [5]. [2.1.1.3] Then the Fourier Laplace transform $p(\bm{\vec{q}},u)$ of the solution to (2.1) is given as [5, 7, 8, 16]

$p(\bm{\vec{q}},u)=\frac{1}{u}\frac{1-\psi(u)}{1-\psi(u)\lambda(k)}=\frac{\Phi(u)}{1-\psi(u)\lambda(\bm{\vec{q}})}$

(2.5)

where $\Phi(u)$ is the Laplace transform of the survival probability.

[2.1.2.1] Similarly the fractional master equation (1.2) can be solved in Fourier-Laplace space with the result

$p(\bm{\vec{q}},u)=\frac{u^{{\omega-1}}}{u^{\omega}-w(\bm{\vec{q}})}$

(2.6)

where $w(\bm{\vec{q}})$ is the Fourier transform of the kernel $w(\bm{\vec{r}})$ in (1.2). [2.1.2.2] Eliminating $p(\bm{\vec{q}},u)$ between (2.5) and (2.6) gives the result

$\frac{1-\psi(u)}{u^{\omega}\psi(u)}=\frac{\lambda(\bm{\vec{q}})-1}{w(\bm{\vec{q}})}=C$

(2.7)

where $C$ is a constant. [2.1.2.3] The last equality obtains because the left hand side of the first equality is $\bm{\vec{q}}$ -independent while the right hand side is independent of $u$ .

[2.1.3.1] From (2.7) it is seen that the fractional master equation characterized by the kernel $w(\bm{\vec{r}})$ and the order $\omega$ corresponds to a special class of space time decoupled continuous time random walks characterized by $\lambda(\bm{\vec{r}})$ and $\psi(t)$ . [2.1.3.2] This correspondence is given precisely as

$\psi(u)=\frac{1}{1+Cu^{\omega}}$

(2.8)

and

$\lambda(\bm{\vec{q}})=1+Cw(\bm{\vec{q}})$

(2.9)

with the same constant $C$ appearing in both equations. [2.2.0.1] Not unexpectedly the correspondence defines the waiting time distribution uniquely up to a constant while the structure function is related to the Fourier transform of the transition rates.

[2.2.1.1] To invert the Laplace transformation in (2.8) and exhibit the form of the waiting time density $\psi(t)$ in the time domain it is convenient to introduce the Mellin transformation

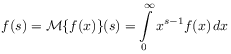$f(s)=\mathcal{M}\{ f(x)\}(s)=\int _{0}^{\infty}x^{{s-1}}f(x)\, dx$

(2.10)

for a function $f(x)$ . [2.2.1.2] The Mellin transformed waiting time density is obtained as

$\psi(s)=\mathcal{M}\{\psi(t)\}(s)=\frac{1}{\omega C^{{1/\omega}}}\left(\frac{1}{C^{{1/\omega}}}\right)^{{-s}}\frac{\Gamma(\frac{1}{\omega}-\frac{s}{\omega})\Gamma(1-\frac{1}{\omega}+\frac{s}{\omega})}{\Gamma(1-s)}$

(2.11)

where $\Gamma(x)$ denotes the Gamma function. [2.2.1.3] To obtain (2.11) from (2.8) the relation between Laplace and Mellin transforms

$\mathcal{M}\{\mathcal{L}\{ f(t)\}(u)\}(s)=\Gamma(s)\mathcal{M}\{ f(t)\}(1-s),$

(2.12)

the special result

$\mathcal{M}\left\{\frac{1}{1+x}\right\}(s)=\Gamma(s)\Gamma(1-s)$

(2.13)

and the general relation

$\mathcal{M}\{ f(ax^{b})\}(s)=\frac{1}{b}a^{{-s/b}}\mathcal{M}\{ f(x)\}(s/b)$

(2.14)

valid for $a,b>0$ have been employed. [2.2.1.4] Using the definition of the general $H$ -function given in the appendix one obtains the result

$\psi(t)=\psi(t;\omega,C)=\frac{1}{\omega C^{{1/\omega}}}H^{{11}}_{{12}}\left(\frac{t}{C^{{1/\omega}}}\left|\begin{array}[]{cc}(1-\frac{1}{\omega},\frac{1}{\omega})\\ (1-\frac{1}{\omega},\frac{1}{\omega})&(0,1)\end{array}\right.\right)$

(2.15)

which may be rewritten as

$\psi(t;\omega,C)=\frac{1}{t}H^{{11}}_{{12}}\left(\frac{t}{C^{{1/\omega}}}\left|\begin{array}[]{cc}(1,1)\\ (1,1)&(1,\omega)\end{array}\right.\right)$

(2.16)

with the help of general relations for $H$ -functions [24]. [2.2.1.5] The dependence on the parameters $\omega$ and $C$ has been indicated explicitly. [2.2.1.6] From the series expansion of $H$ -functions given in the appendix one finds

[page 3, §0]

$\psi(t;\omega,C)=\frac{t^{{\omega-1}}}{C}\sum _{{k=0}}^{{\infty}}\frac{1}{\Gamma(\omega k+\omega)}\left(-\frac{t^{\omega}}{C}\right)^{k}$

(2.17)

showing that $\psi(t)$ behaves as

$\psi(t)\propto t^{{-1+\omega}}$

(2.18)

for small $t\rightarrow 0$ . [3.1.0.1] Because $0<\omega\leq 1$ the waiting time density is singular at the origin. [3.1.0.2] The series representation (2.17) shows that the waiting time density is a natural generalization of an exponential waiting time density to which it reduces for $\omega=1$ , i.e. $\psi(t;1,C)=(1/C)\exp(t/C)$ . [3.1.0.3] The series in (2.17) is recognized as the generalized Mittag-Leffler function $E_{{\omega,\omega}}(x)$ [25], and $\psi(t)$ may thus be written alternatively as

$\psi(t;\omega,C)=\frac{t^{{\omega-1}}}{C}E_{{\omega,\omega}}\left(-\frac{t^{\omega}}{C}\right).$

(2.19)

[3.1.0.4] Of course the result (2.17) can also be obtained more directly, but we have presented here a method using Mellin transforms because it remains applicable in cases where a direct inversion fails [23]. [3.1.0.5] The asymptotic expansion of the Mittag-Leffler function for large argument [25] yields

$\psi(t)\propto t^{{-1-\omega}}$

(2.20)

for large $t\rightarrow\infty$ and $0<\omega<1$ . [3.1.0.6] This result shows that the waiting time distribution has an algebraic tail of the kind usually considered in the theory of random walks [12, 13, 14, 15, 16].

Author:	R. Hilfer and L. Anton
originally published in:	Physical Review E 51, R848 (1995)
originally submitted:	October 28th, 1994