2 Percolating versus nonpercolating fluid regions

[3.0.1.1] The necessity to distinguish between percolating and nonpercolating fluid regions arises from the fact that in static equilibrium the pressure can become hydrostatic only in those fluid regions that are connected (or percolating) to the sample boundary [14, 16, 15]. [3.0.1.2] Each of the two fluids $\mathbb{W},\mathbb{O}$ consists of disjoint and pathconnected subsets (regions) $\mathbb{W}_{i},\mathbb{O}_{i}$ . [3.0.1.3] More precisely one has

$\displaystyle\mathbb{W}$	$\displaystyle=\bigcup _{{i=1}}^{{{N_{\mathbb{W}}}}}\mathbb{W}_{i}$		(14a)
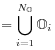$\displaystyle\mathbb{O}$	$\displaystyle=\bigcup _{{i=1}}^{{{N_{\mathbb{O}}}}}\mathbb{O}_{i}$		(14b)

where the subsets $\mathbb{W}_{i},\mathbb{O}_{i}$ are mutually disjoint, and each of them is pathconnected. [3.0.1.4] A set is called pathconnected if any two of its points can be connected by a path contained inside the set. [3.0.1.5] The sets are called mutually disjoint if $\mathbb{O}_{i}\cap\mathbb{O}_{j}=\emptyset$ and $\mathbb{W}_{i}\cap\mathbb{W}_{j}=\emptyset$ holds for all $i\neq j$ . [3.0.1.6] The integers ${N_{\mathbb{W}}},{N_{\mathbb{O}}}$ give the total number of pathconnected subsets for water resp. oil. [3.0.1.7] Of course, these numbers change with time as do the regions $\mathbb{W}_{i},\mathbb{O}_{i}$ .

[3.0.2.1] Now define percolating ( $\mathbb{F}_{1},\mathbb{F}_{3}$ ) and nonpercolating ( $\mathbb{F}_{2},$ $\mathbb{F}_{4}$ ) fluid regions by classifying the subsets $\mathbb{W}_{i},\mathbb{O}_{i}$ as to whether they have empty or nonempty intersection with the sample boundary $\partial\mathbb{S}$ . [3.1.0.1] More formally, define

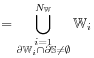$\displaystyle\mathbb{F}_{1}$	$\displaystyle=\bigcup^{{N_{\mathbb{W}}}}_{{\substack{i=1\\ \partial\mathbb{W}_{i}\cap\partial\mathbb{S}\neq\emptyset}}}\mathbb{W}_{i}$	(15a)
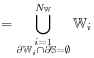$\displaystyle\mathbb{F}_{2}$	$\displaystyle=\bigcup^{{N_{\mathbb{W}}}}_{{\substack{i=1\\ \partial\mathbb{W}_{i}\cap\partial\mathbb{S}=\emptyset}}}\mathbb{W}_{i}$	(15b)
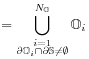$\displaystyle\mathbb{F}_{3}$	$\displaystyle=\bigcup^{{N_{\mathbb{O}}}}_{{\substack{i=1\\ \partial\mathbb{O}_{i}\cap\partial\mathbb{S}\neq\emptyset}}}\mathbb{O}_{i}$	(15c)
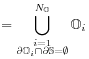$\displaystyle\mathbb{F}_{4}$	$\displaystyle=\bigcup^{{N_{\mathbb{O}}}}_{{\substack{i=1\\ \partial\mathbb{O}_{i}\cap\partial\mathbb{S}=\emptyset}}}\mathbb{O}_{i}$	(15d)

so that $\mathbb{F}_{1}$ is the union of all regions $\mathbb{W}_{i}$ , and is $\mathbb{F}_{3}$ the union of all regions $\mathbb{O}_{i}$ , that have nonempty intersection with the sample boundary $\partial\mathbb{S}$ . [3.1.0.2] Similarly $\mathbb{F}_{2}$ is the union of all regions $\mathbb{W}_{i}$ that have empty intersection with $\partial\mathbb{S}$ , and similarly for $\mathbb{F}_{4}$ . [3.1.0.3] In this way each point in $\mathbb{P}$ belongs to one of four regions $\mathbb{F}_{i}$ , $i=1,2,3,4$ . [3.1.0.4] This results in a total of four fluid phases called percolating resp. nonpercolating water, and percolating resp. nonpercolating oil. [3.1.0.5] The index $i=5$ will be used for the rigid matrix (=rock).

Author:	R. Hilfer
originally published in:	Physical Review E 73, 016307 (2006)
originally submitted:	20. 05. 2005