4 Identification of capillary pressure
4.1 Hydrostatic equilibrium
[5.0.1.1] The constitutive theory proposed above, contrary to the
traditional theory, does not postulate a unique
capillary pressure as a constitutive parameter function.
[5.0.1.2] On the other hand experimental evidence suggests that
capillary pressure is a useful concept to correlate
observations.
[5.0.1.3] To make contact with the established traditional theory
it is therefore important to check
whether the traditional
![]() relation
can be viewed as a derived concept within the new theory.
relation
can be viewed as a derived concept within the new theory.
[5.0.2.1] Consider first the case of hydrostatic equilibrium
where ![]() for all
for all ![]() .
[5.0.2.2] In hydrostatic equilibrium all fluids are at rest.
[5.0.2.3] In this case the traditional theory implies
.
[5.0.2.2] In hydrostatic equilibrium all fluids are at rest.
[5.0.2.3] In this case the traditional theory implies
![]() and
and ![]() ,
by mass balance eq. (11).
[5.0.2.4] The traditional momentum balance
eqs. (12) can be integrated to give
,
by mass balance eq. (11).
[5.0.2.4] The traditional momentum balance
eqs. (12) can be integrated to give
| (31a) | |||
| (31b) |
where ![]() is a point in the boundary.
[5.0.2.5] Combined with the assumption (13) one finds
is a point in the boundary.
[5.0.2.5] Combined with the assumption (13) one finds
| (32) | |||
implying the existence of a unique
hydrostatic saturation profile ![]() .
[5.0.2.6] Here
.
[5.0.2.6] Here ![]() is the capillary pressure at
is the capillary pressure at ![]() .
[5.0.2.7] Experiments show, however, that hydrostatic saturation profiles
are not unique.
[5.0.2.8] As a consequence the traditional theory employs
multiple
.
[5.0.2.7] Experiments show, however, that hydrostatic saturation profiles
are not unique.
[5.0.2.8] As a consequence the traditional theory employs
multiple ![]() relations for drainage and
imbibition, and this leads to difficult problems
when imbibition and drainage occur simultaneously.
relations for drainage and
imbibition, and this leads to difficult problems
when imbibition and drainage occur simultaneously.
[5.0.3.1] The nonlinear theory proposed here can be solved in the
special case of hydrostatic equilibrium.
[5.0.3.2] Mass balance (1) now implies
![]() for all
for all ![]() .
[5.0.3.3] Integrating eqs. (2) yields
.
[5.0.3.3] Integrating eqs. (2) yields
| (33a) | |||
| (33b) | |||
| (33c) | |||
| (33d) | |||
If one identifies ![]() with
with ![]() and
and ![]() with
with ![]() then
eqs. (33a)
and (33b) suggest to identify
then
eqs. (33a)
and (33b) suggest to identify
![]() as
as ![]() .
[5.1.0.1] Then eqs. (33c) and (33d)
combined with
.
[5.1.0.1] Then eqs. (33c) and (33d)
combined with
![]() and
and ![]() imply
imply
![]() .
[5.1.0.2] The capillary pressure
.
[5.1.0.2] The capillary pressure ![]() depends not only
on
depends not only
on ![]() but also on
but also on ![]() and
and ![]() in hydrostatic equilibrium.
[5.1.0.3] In the theory proposed here it is not possible to identify
a unique
in hydrostatic equilibrium.
[5.1.0.3] In the theory proposed here it is not possible to identify
a unique ![]() relation when all fluids are at rest.
This agrees with experiment.
relation when all fluids are at rest.
This agrees with experiment.
4.2 Residual decoupling approximation
[5.1.1.1]
While it is not possible to identify a unique ![]() relation in hydrostatic equilibrium such a functional relation
emerges nevertheless from the present theory when the
system approaches hydrostatic equilibrium
in the residual decoupling approximation.
[5.1.1.2] The approach to hydrostatic equilibrium in
the residual decoupling approximation (RDA)
can be formulated mathematically
as
relation in hydrostatic equilibrium such a functional relation
emerges nevertheless from the present theory when the
system approaches hydrostatic equilibrium
in the residual decoupling approximation.
[5.1.1.2] The approach to hydrostatic equilibrium in
the residual decoupling approximation (RDA)
can be formulated mathematically
as ![]() and
and ![]() .
[5.1.1.3] In addition it is assumed that the velocities
.
[5.1.1.3] In addition it is assumed that the velocities ![]() are small but nonzero.
[5.1.1.4] In the RDA mass balance becomes
are small but nonzero.
[5.1.1.4] In the RDA mass balance becomes
| (34a) | |||
| (34b) | |||
| (34c) | |||
| (34d) |
Momentum balance becomes in the RDA
| (35a) | |||
| (35b) | |||
| (35c) | |||
| (35d) |
where the abbreviations
| (36a) | |||
| (36b) |
were used.
[5.1.1.5] Equations (34) and (35)
together with eq.(16b) provide
17 equations for 12 variables (![]() and
and ![]() ).
).
[5.1.2.1] Equations (34) and (35)
can now be compared to the traditional equations
(11)–(13) with the aim
of identifying capillary pressure and relative
permeability.
[5.1.2.2] Consider first the momentum balance eqs. (35).
[5.1.2.3] As in the traditional theory [24] viscous decoupling
is assumed to hold, i.e. ![]() and
and ![]() .
[5.1.2.4] Next, assuming that
.
[5.1.2.4] Next, assuming that
![]() ,
, ![]() , and
, and ![]() one finds
[page 6, §0]
one finds
[page 6, §0]
| (37a) | |||
| (37b) | |||
| (37c) | |||
| (37d) |
where barycentric velocities
![]() defined through
defined through
| (38a) | |||
| (38b) |
have been introduced. [6.0.0.1] Subtracting eq. (37a) from eq. (37c), as well as eq. (37d) from eq. (37b), and equating the result gives
| (39) |
where eq. (22) has also been employed. [6.0.0.2] This result can be compared to the traditional theory where one finds from eqs. (12) and (13)
| (40) |
Again this seems to imply ![]() as already found above for hydrostatic equilibrium.
[6.0.0.3] However, within the RDA additional constraints follow
from mass balance (34).
as already found above for hydrostatic equilibrium.
[6.0.0.3] However, within the RDA additional constraints follow
from mass balance (34).
[6.0.1.1] First, observe that adding (34a) to (34b) resp. (34c) to (34d) with the help of eq. (38a) yields the traditional mass balance eqs. (11). [6.0.1.2] Next, verify by insertion that eqs. (34b) and (34d) admit the solutions
| (41a) | |||
| (41b) | |||
where the displacement process is assumed to start from the initial conditions
| (42a) | |||
| (42b) | |||
| (42c) |
at some initial instant ![]() .
[6.1.0.1] The limiting saturations
.
[6.1.0.1] The limiting saturations ![]() ,
, ![]() ,
, ![]() are given by eqs. (29).
[6.1.0.2] They depend only on the sign of
are given by eqs. (29).
[6.1.0.2] They depend only on the sign of
![]() if
if
![]() can be assumed to hold.
[6.1.0.3] One finds in this case
can be assumed to hold.
[6.1.0.3] One finds in this case
| (43a) | |||
| (43b) | |||
| (43c) | |||
| (43d) |
for imbibition processes (i.e. ![]() ), resp.
), resp.
| (44a) | |||
| (44b) | |||
| (44c) | |||
| (44d) |
for drainage processes (i.e. ![]() ).
).
[6.1.1.1] With these solutions in hand the capillary pressure can be identified up to a constant as
| (45) | |||
where ![]() and
and ![]() are given by eqs. (41).
[6.1.1.2] This result holds in the RDA combined with
the assumptions above.
[6.1.1.3] Furthermore, equations (37a) and (37c)
are recognized as generalized Darcy laws with relative permeabilities
identified as
are given by eqs. (41).
[6.1.1.2] This result holds in the RDA combined with
the assumptions above.
[6.1.1.3] Furthermore, equations (37a) and (37c)
are recognized as generalized Darcy laws with relative permeabilities
identified as
| (46a) | |||
| (46b) |
where ![]() and
and ![]() are again given by eqs. (41).
are again given by eqs. (41).
4.3 Reproduction of experimental observations
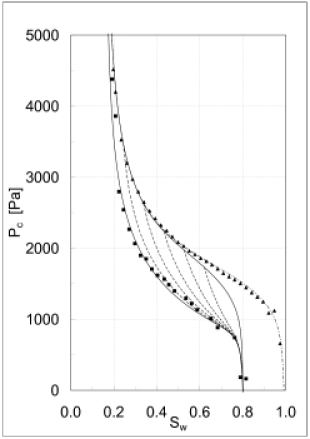
[6.1.2.1] Figure 1 visualizes the results obtained by fitting
eq. (45) to experiment.
[6.1.2.2] The experimental results are depicted as
triangles (primary drainage) and squares (imbibition).
[6.1.2.3] The experiments were performed in a medium grained
unconsolidated water wet sand of porosity ![]() .
[6.1.2.4] Water was used as wetting fluid while air
resp. TCE were used as the nonwetting fluid.
[6.1.2.5] The experiments were carried out over a period of
several weeks at the Versuchseinrichtung zur Grundwasser-
und Altlastensanierung (VEGAS)
[page 7, §0] at the Universität Stuttgart.
[7.0.0.1] They are described in more detail in Ref. [25].
The parameters for all the curves shown in all four
figures are
.
[6.1.2.4] Water was used as wetting fluid while air
resp. TCE were used as the nonwetting fluid.
[6.1.2.5] The experiments were carried out over a period of
several weeks at the Versuchseinrichtung zur Grundwasser-
und Altlastensanierung (VEGAS)
[page 7, §0] at the Universität Stuttgart.
[7.0.0.1] They are described in more detail in Ref. [25].
The parameters for all the curves shown in all four
figures are
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() Pa,
Pa,
![]() Pa, and
Pa, and
![]() Pa
Pa
![]() Pa.
Pa.
[7.0.1.1] If it is further assumed that the medium is isotropic and
that the matrices ![]() have the form
have the form
| (47a) | |||
| (47b) |
then the relative permeability functions are
obtained from eqs. (46).
[7.0.1.2] The result for the special case ![]() is shown
in Figures 3 and 4.
[7.0.1.3] The parameters
is shown
in Figures 3 and 4.
[7.0.1.3] The parameters ![]() are chosen such that
are chosen such that ![]() and
and
![]() ,
where
,
where ![]() are the fluid viscosities
and
are the fluid viscosities
and ![]() is the absolute permeability of the medium.
[7.0.1.4] All other parameters for the relative permeability
functions shown in Figures 3 and 4
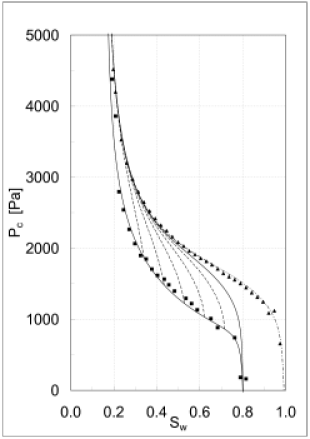
are identical to those of the capillary pressure curves
in Figures 1 and 2.
is the absolute permeability of the medium.
[7.0.1.4] All other parameters for the relative permeability
functions shown in Figures 3 and 4
are identical to those of the capillary pressure curves
in Figures 1 and 2.
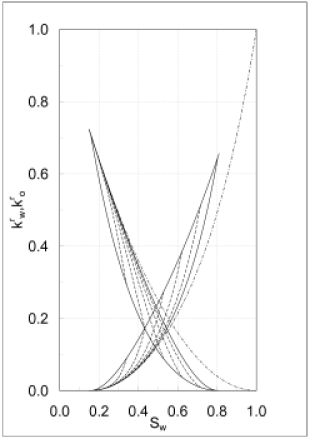
[7.0.2.1] Note that Figures 1 through 4 show
a total of 30 different scanning curves, 5 drainage
and 5 imbibition scanning curves each for
![]() and
and ![]() .
[7.1.0.1] In addition a total of 9 different bounding curves
are displayed, namely
the primary drainage, secondary drainage and
secondary imbibition curve for
.
[7.1.0.1] In addition a total of 9 different bounding curves
are displayed, namely
the primary drainage, secondary drainage and
secondary imbibition curve for ![]() and
and ![]() .
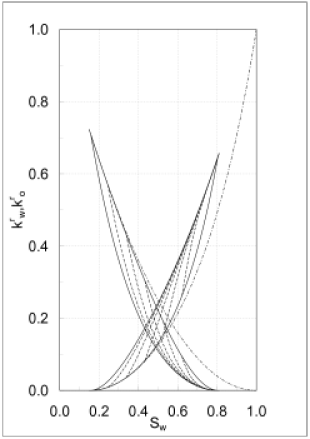
[7.1.0.2] Three more bounding curves namely primary imbibition
for
.
[7.1.0.2] Three more bounding curves namely primary imbibition
for ![]() and
and ![]() starting from
starting from ![]() are not shown because they are difficult to obtain
experimentally for a water-wet sample.
[7.1.0.3] Of course the number of scanning curves
can be increased indefinitely.
[7.1.0.4] All of these curves have the same
values of the constitutive parameters.
[7.1.0.5] There is less than one parameter per curve.
[7.1.0.6] The curves shown in the figures exhibit the full range
of hysteretic phenomena known from experiment.
[7.1.0.7] Nevertheless it should be kept in mind that these
curves are obtained only under special approximations,
and when these are not valid such curves do not exist.
are not shown because they are difficult to obtain
experimentally for a water-wet sample.
[7.1.0.3] Of course the number of scanning curves
can be increased indefinitely.
[7.1.0.4] All of these curves have the same
values of the constitutive parameters.
[7.1.0.5] There is less than one parameter per curve.
[7.1.0.6] The curves shown in the figures exhibit the full range
of hysteretic phenomena known from experiment.
[7.1.0.7] Nevertheless it should be kept in mind that these
curves are obtained only under special approximations,
and when these are not valid such curves do not exist.