2 Formulation of the Model
2.1 Correlated Hopping in a Frozen Percolation Network
[179.1.1] Consider the random walk of a single particle of type A
in a percolating network on a regular lattice.
[179.1.2] We will always take the lattice constant of the
underlying lattice to be unity.
[179.1.3] For simplicity we consider the case of bond percolation
instead of site percolation.
[179.1.4] That is, the bonds of the regular lattice
are assumed to be blocked be B-particles (blockers) with probability ![]() .
[179.1.5] If a bond is blocked by a B-particle
it cannot be crossed by the A-particle (walker).
[179.1.6] We assume that the walker has a memory of its previous step.
[179.1.7] It returns with a transition rate
.
[179.1.5] If a bond is blocked by a B-particle
it cannot be crossed by the A-particle (walker).
[179.1.6] We assume that the walker has a memory of its previous step.
[179.1.7] It returns with a transition rate ![]() , to the previously visited site,
and jumps with a rate
, to the previously visited site,
and jumps with a rate ![]() to any other of the nearest neighbour sites.
[179.1.8] The ratio
to any other of the nearest neighbour sites.
[179.1.8] The ratio ![]() is a measure of the strength of the memory correlations.
[179.1.9] For
is a measure of the strength of the memory correlations.
[179.1.9] For ![]() the walker returns preferentially to its previously visited site,
and we will refer to this case as “enhanced reversals”.
[179.1.10] In the case
the walker returns preferentially to its previously visited site,
and we will refer to this case as “enhanced reversals”.
[179.1.10] In the case ![]() the walker tends to avoid the previously visited site
and this will be termed “reduced reversals”.
[179.1.11] As usual, we are interested in the autocorrelation function
the walker tends to avoid the previously visited site
and this will be termed “reduced reversals”.
[179.1.11] As usual, we are interested in the autocorrelation function ![]() ,
i. e. the probability density to find the walker at site
,
i. e. the probability density to find the walker at site ![]() at time
at time ![]() if it started from site
if it started from site ![]() at time
at time ![]() .
[179.1.12] We will show below that the problem can be formulated
as a system of second order equations for the
.
[179.1.12] We will show below that the problem can be formulated
as a system of second order equations for the ![]() which reads
which reads
| (2.1a) | |
where ![]() and
and ![]() is the coordination number of site
is the coordination number of site ![]() .
[179.1.13] The symmetric quantities
.
[179.1.13] The symmetric quantities ![]() represent the bond disorder and are defined as
represent the bond disorder and are defined as
| (2.2a) | |
[page 180, §0]
[180.0.1] The summation in eq. (2.1a)
runs over the nearest neighbour sites ![]() of site
of site ![]() .
[180.0.2] Note that in the uncorrelated case,
.
[180.0.2] Note that in the uncorrelated case, ![]() , eq. (2.1)
reduces to the usual master equation for a random walk
on a bond percolation network if one replaces
, eq. (2.1)
reduces to the usual master equation for a random walk
on a bond percolation network if one replaces ![]() by the sum of
by the sum of ![]() and its derivative.
and its derivative.
[180.1.1] Equation (2.1) has to be supplemented by initial conditions
for ![]() and its derivative.
[180.1.2] Special attention has to be paid
to the condition on
and its derivative.
[180.1.2] Special attention has to be paid
to the condition on ![]() and its derivative.
[180.1.3] The correct choice is
and its derivative.
[180.1.3] The correct choice is
| (2.3a) | |||
| (2.3b) |
where the symbol ![]() stands for the limit
stands for the limit ![]() from above.
[180.1.4] Note that
from above.
[180.1.4] Note that ![]() is the average transition rate
out of the starting point.
is the average transition rate
out of the starting point.
[180.2.1] We now derive eq. (2.1) as the equations of motion
for our correlated random walk.
[180.2.2] This will be done by a suitable reformulation of the equations
for the correlated random walk on the regular lattice[19],
and subsequent generalization to the disordered case.
[180.2.3] Consider therefore the random walker on a regular lattice.
[180.2.4] The random walker has a memory of its previous step
and as a consequence its walk is not markovian,
i. e. the transition probabilities are not completely determined
by the currently occupied site.
[180.2.5] However a markovian description can be obtained
by introducing an enlarged state space with internal states
which correspond to the previously occupied sites[21].
[180.2.6] Therefore the central quantity is the probability density ![]() to find the walker at site
to find the walker at site ![]() at time
at time ![]() given that it arrived at
given that it arrived at ![]() via a direct transition from site
via a direct transition from site ![]() .
[180.2.7] Thus
.
[180.2.7] Thus ![]() labels the previously occupied site or history.
[page 181, §0]
[181.0.1] Then the symmetric probablity density
labels the previously occupied site or history.
[page 181, §0]
[181.0.1] Then the symmetric probablity density ![]() is obtained from
is obtained from ![]() by a summation over all possible histories
by a summation over all possible histories
| (2.4) |
where the sum runs over all nearest neighbour sites ![]() of site
of site ![]() .
[181.0.2] The conditional probability densities
.
[181.0.2] The conditional probability densities ![]() obey the master equation
obey the master equation
| (2.5) |
where the sum runs over all nearest neighbours ![]() of site
of site ![]() except for site
except for site ![]() on the regular lattice.
[181.0.3] This is the starting point for deriving eq. (2.1).
on the regular lattice.
[181.0.3] This is the starting point for deriving eq. (2.1).
[181.1.1] Equation (2.5) can now be reformulated by first writing it in a more symmetric form. [181.1.2] Using eq. (2.4) we can rewrite eq. (2.5) as
| (2.6) |
where ![]() , and
, and ![]() denotes the coordination number of the lattice.
[181.1.3] Note that eq. (2.6) reduces to the master equation
for a random walk on a regular lattice if one sets
denotes the coordination number of the lattice.
[181.1.3] Note that eq. (2.6) reduces to the master equation
for a random walk on a regular lattice if one sets ![]() and sums over all sites
and sums over all sites ![]() which are nearest neighbours of site
which are nearest neighbours of site ![]() .
[181.1.4] Next we differentiate eq. (2.6) and sum over
.
[181.1.4] Next we differentiate eq. (2.6) and sum over ![]() .
[181.1.5] We then employ it for
.
[181.1.5] We then employ it for ![]() and
and ![]() interchanged
to eliminate the term
interchanged
to eliminate the term ![]() and find
and find
| (2.7) |
[181.1.6] Solving eq. (2.6) for ![]() and inserting the result into eq. (2.7)
one obtains a closed second order equation for
and inserting the result into eq. (2.7)
one obtains a closed second order equation for ![]()
| (2.8) |
where the summations, as before,
run over all nearest neighbour sites ![]() of site
of site ![]() .
[page 182, §0]
[182.0.1] Eq. (2.8) contains the same information as eq. (2.5)
but no longer involves the directional quantities
.
[page 182, §0]
[182.0.1] Eq. (2.8) contains the same information as eq. (2.5)
but no longer involves the directional quantities ![]() .
[182.0.2] This form can now be used to introduce disorder
and it leads directly to eq. (2.1).
[182.0.3] We now turn to the introduction of a time dependent network.
.
[182.0.2] This form can now be used to introduce disorder
and it leads directly to eq. (2.1).
[182.0.3] We now turn to the introduction of a time dependent network.
2.2 Correlated Hopping in a Dynamic Percolation Network
[182.1.1] Consider a system where the configuration of accessible sites fluctuates in time.
[182.1.2] We are interested in the case where the B-particles perform a random walk.
[182.1.3] Because we are dealing with bond percolation
this random walk occurs on the dual lattice.
[182.1.4] In an elementary step a blocking bond swings around either one of its end points
through an angle ![]() where
where ![]() is the coordination number of the underlying lattice.
[182.1.5] It then occupies the new bond position if it is vacant.
[182.1.6] This process is repeated on the average after a time
is the coordination number of the underlying lattice.
[182.1.5] It then occupies the new bond position if it is vacant.
[182.1.6] This process is repeated on the average after a time ![]() which is the characteristic time scale for the blocker motion.
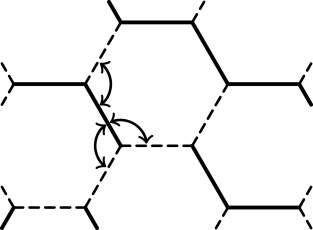
[182.1.7] In Figure 1 we depict the possible rotations
of a B-particle for the case of a hexagonal lattice.
[182.1.8] This model has been termed “dynamic bond percolation” model[22].
[182.1.9] The characteristic hopping time for a single B-particle is called
which is the characteristic time scale for the blocker motion.
[182.1.7] In Figure 1 we depict the possible rotations
of a B-particle for the case of a hexagonal lattice.
[182.1.8] This model has been termed “dynamic bond percolation” model[22].
[182.1.9] The characteristic hopping time for a single B-particle is called ![]() .
[182.1.10] The ratio
.
[182.1.10] The ratio ![]() between the typical hopping time
of the blockers and the walker
will be the main variable characterizing the dynamics of the environment.
between the typical hopping time
of the blockers and the walker
will be the main variable characterizing the dynamics of the environment.
[182.2.1] Equation (2.1) must be generalized to allow for time dependent transition rates. [182.2.2] Therefore we have to consider an equation of the form
| (2.9a) |
where now the coefficients ![]() are time dependent,
are time dependent,
| (2.10a) |
[page 183, §0] [183.0.1] The time dependence of these coefficients could in principle be determined from the many particle master equation for all blockers. [183.0.2] However, because that equation is much too complicated we will approximate the true time dependence by a simple renewal model in Section 4. [183.0.3] Equation (2.9) completes the formulation of the model. [183.0.4] We remark here that other forms of a two step memory are possible and may be useful for applications. [183.0.5] For example one can consider enhanced or reduced transitions continuing in the same direction as the last step. [183.0.6] Such correlations lead to more complicated equations, but they can be treated by the same general approach presented here.
[183.1.1] We conclude this section with the formulas that will be used to calculate
the frequency dependent conductivity ![]() from
from ![]() .
[183.1.2] This is done via a generalized Einstein relation which reads
.
[183.1.2] This is done via a generalized Einstein relation which reads
| (2.11a) | |
where ![]() is the carrier density,
is the carrier density,
![]() their electric charge,
their electric charge, ![]() , the Boltzmann constant,
, the Boltzmann constant,
![]() the absolute tempreature, and
the absolute tempreature, and ![]() the generalized frequency dependent diffusion coefficient.
[page 184, §0]
[184.0.1]
the generalized frequency dependent diffusion coefficient.
[page 184, §0]
[184.0.1] ![]() will be calculated in standard fashion from[23]
will be calculated in standard fashion from[23]
| (2.12a) | |
where ![]() is the solution
to eq. (2.9) or eq. (2.1) for the frozen case.
[184.0.2] The latter will be determined in the next section.
is the solution
to eq. (2.9) or eq. (2.1) for the frozen case.
[184.0.2] The latter will be determined in the next section.
